Sucking creates a vacuum in the drinking straw, so that the greater ambient pressure pushes the beverage through the drinking straw.
Indroduction
Drinking out of a straw sounds quite simple at first. One end of the straw is placed in a water-filled glass and at the other end the water is sucked up into the mouth. One might think that such a drinking straw could in principle be of any length. In order to overcome any large differences in height, one would only have to suck on it powerfully enough. Practice shows, however, that with increasing height it becomes more and more difficult to get the liquid through the straw. Eventually it will no longer be possible to drink water from such a drinking straw from a height of about 10 metres. Even the most powerful vacuum pump in the world would not be able to pump water to such a height!
In fact, it is not the generation of negative pressure during suction that is the limiting factor, but the ambient pressure! Without the atmospheric pressure it would not be possible to drink from a straw (this also applies to suction pumps). The principle of drinking with a straw and the operation of suction pumps and the associated limited suction lift are explained in more detail in this article.

Working principle
First imagine a glass of water. In the glass there is a round plate which lies directly on the surface of the water. In the middle of the plate is a hole through which a drinking straw is led into the water. If the plate is pressed downwards, the water is pressed upwards through the straw.

In the same way the ambient pressure on the water surface is able to push the water upwards through the drinking straw. However, if the straw is simply placed in the water, then the force with which the external ambient pressure tries to push the water upwards (as in the example above with the plate) is as great as the force with which the internal ambient pressure inside the straw pushes the water downwards.
If the water is to be lifted, the air pressure inside the straw must be lowered compared to the external atmospheric pressure. This creates a lower counterforce so that the force of the external ambient pressure is able to push the water upwards. The lowering of the internal air pressure in the drinking straw is done by sucking at its opening, so that the air particles inside are sucked off. This causes a negative pressure inside the straw. In this way, the water is pushed upwards by the greater external ambient pressure against the lower pressure inside the drinking straw.
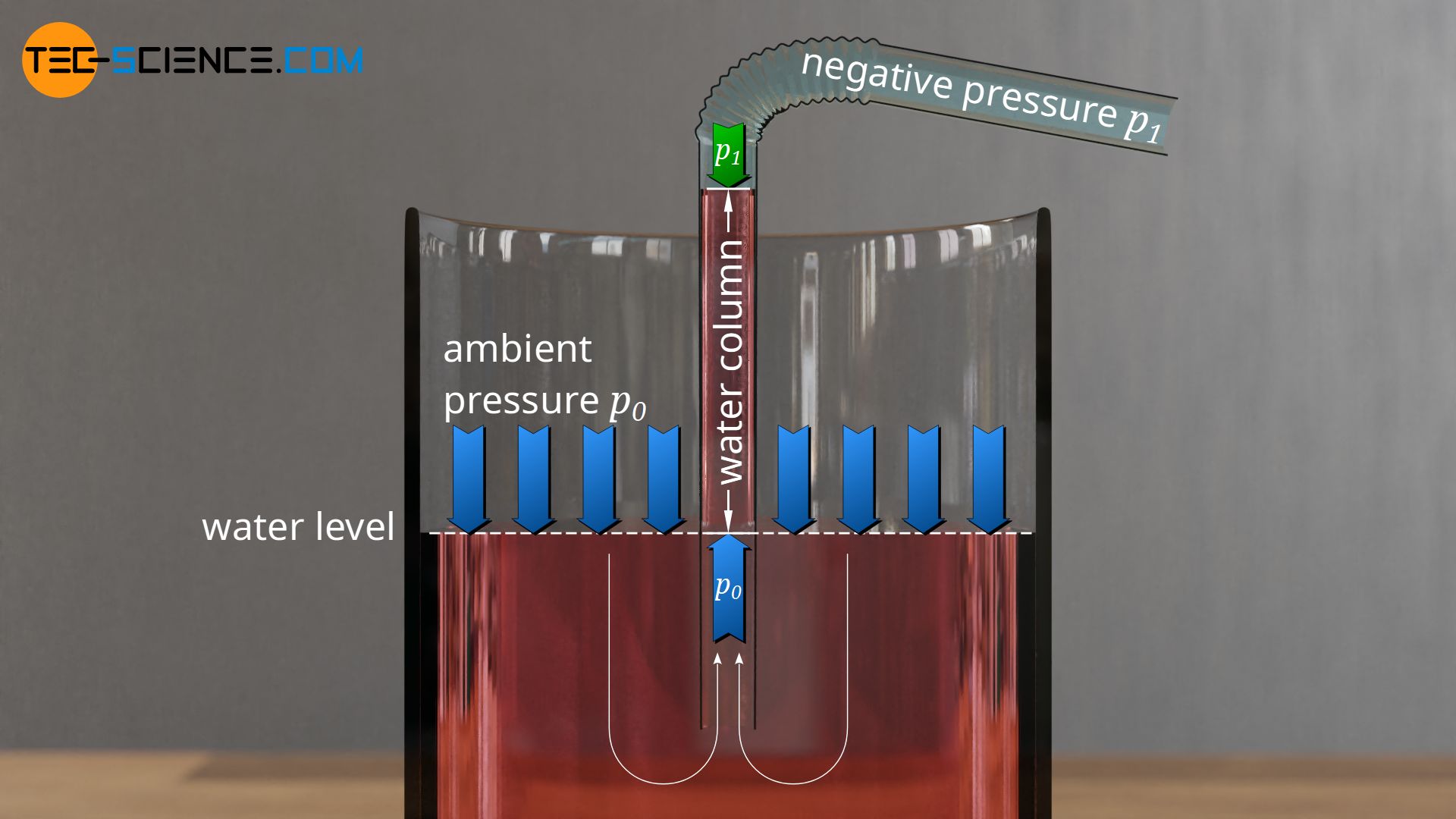
Thus it is the atmospheric pressure that makes it possible for the water in the drinking straw to be pushed upwards. Creating the negative pressure in the drinking straw is only a means to an end, so to speak. If, on the other hand, no ambient pressure existed (vacuum), the water could no longer be pushed upwards by any air particles. For this reason it is not possible to drink a glass of water with the help of a straw even in free space (apart from the fact that water would immediately become gaseous anyway due to the vacuum)!
Maximum suction lift
As already mentioned in the introductory section, from a certain height to be overcome between the surface of the water and the mouth, one will notice that it is no longer possible to drink from the drinking straw, no matter how hard one tries. In theory, this maximum suction lift is around 10 m for water. This does not have to do with a too weakly developed mouth musculature but has a natural physical cause. Even the most powerful suction pump in the world would not be able to overcome a height difference of more than 10 metres if a perfect vacuum were created. This maximum suction height will be derived mathematically in the following.
The force Fp with which the water can be effectively pushed upwards is the difference between the forces acting at the lower end (F0) and the upper end of the water column (F1). The water column is the water in the straw relative to the water level in the glass. At this level, the ambient pressure p0 also acts in the water itself (since there is no hydrostatic pressure at this point). The immersion depth of the drinking straw plays no role (more about this later).
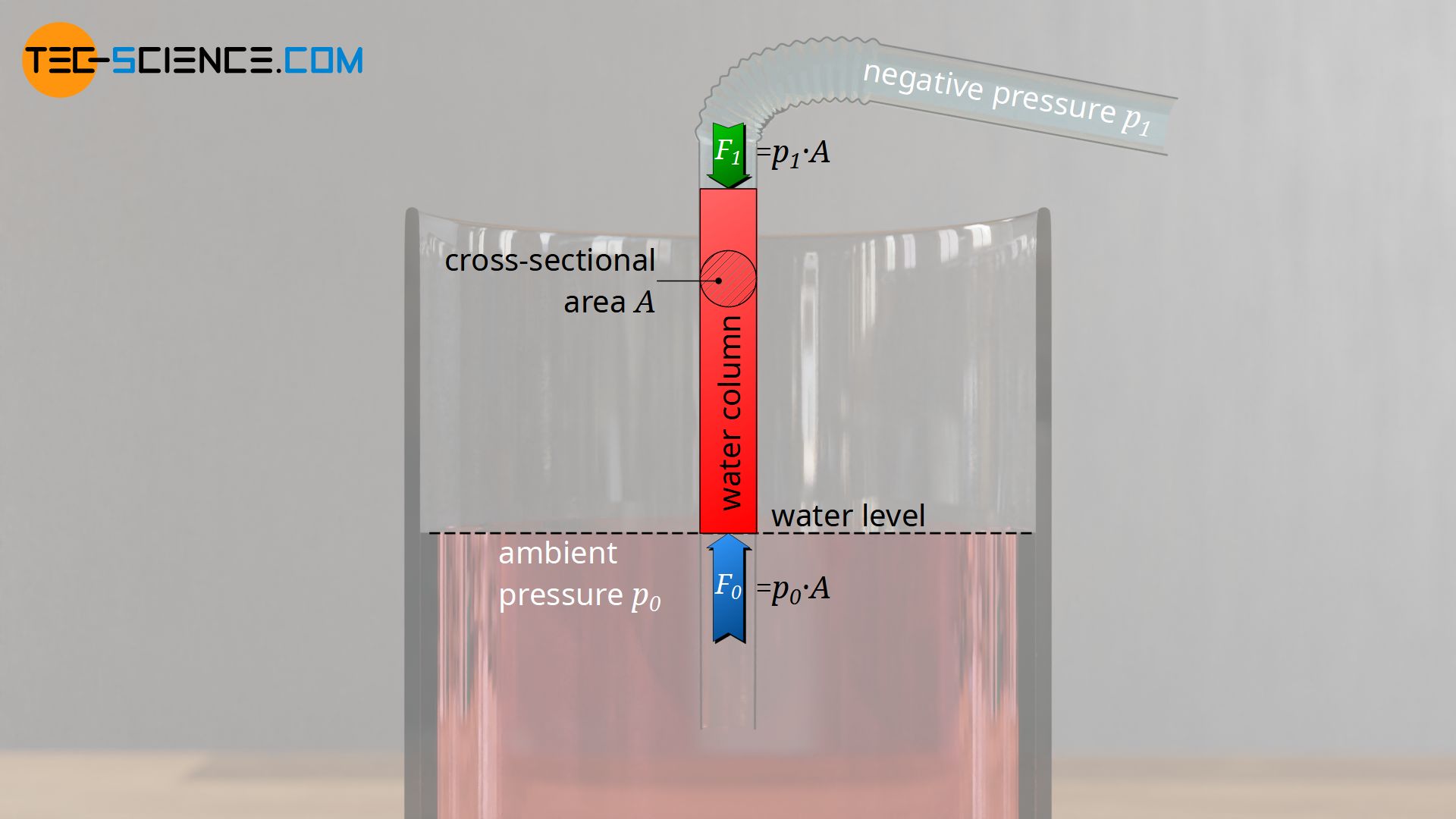
The resultant upward force Fp results from the difference between the force F0 at the lower end of the water column which pushes the water upwards by the ambient pressure p0 and the force F1 at the upper end of the water column which pushes the water downwards by the internal drinking straw pressure p1. In both cases, the pressures act on the same inner straw cross section A so that the corresponding forces can be determined from the pressures (F=p⋅A).
\begin{align}
&F_p = F_0 – F_1 \\[5px]
&F_p = p_0 \cdot A – p_1 \cdot A \\[5px]
\label{ff}
&\underline{F_p = \left(p_0 – p_1 \right) \cdot A} \\[5px]
\end{align}
This force Fp must obviously be so large that it is able to push the water column with the weight Fg=m⋅g upwards. The weight of the water column to be pushed up depends on the water level in the straw. The weight increases with increasing height. This weight can be determined from the cross-sectional area A of the water column (= cross-sectional area of the straw) and the water density ϱ as follows:
\begin{align}
&F_g = m \cdot g ~~~~~\text{and} ~~~ m = \rho V = \rho A h \\[5px]
&\underline{F_g = \rho gh \cdot A} \\[5px]
\end{align}
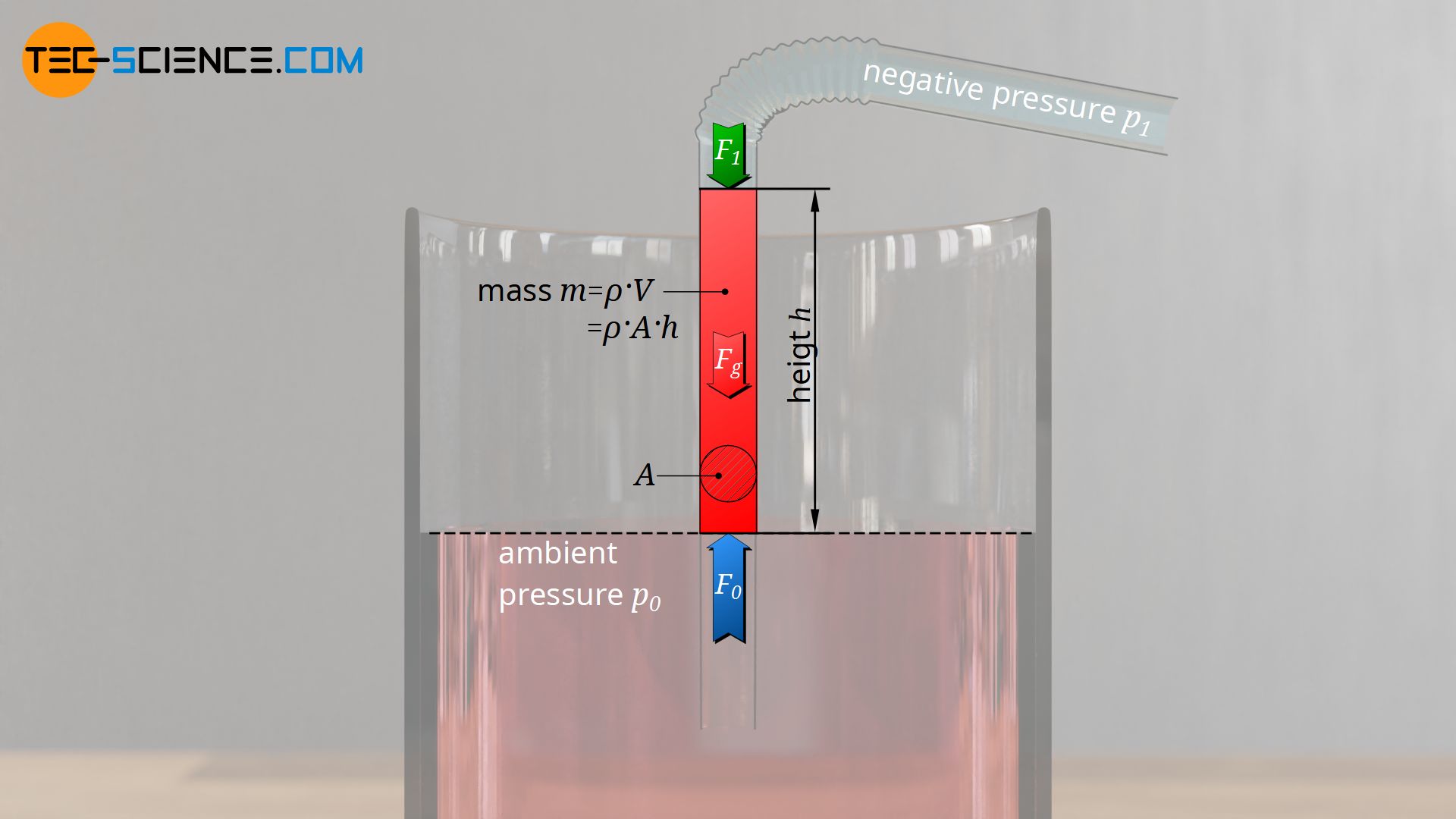
As the water level in the straw increases, the weight of the water column increases. At some point the weight Fg will eventually become as large as the upwards acting force Fp. In this state it is no longer possible to push the water further upwards. At given pressures this suction height h is determined as follows:
\begin{align}
\require{cancel}
F_p &\overset{!}{=} F_g \\[5px]
\left(p_0 – p_1 \right) \cdot \bcancel{A} & = \rho gh \cdot \bcancel{A} \\[5px]
p_0 – p_1 &= \rho h g \\[5px]
\end{align}
\begin{align}
&\underline{h = \frac{p_0 – p_1}{\rho g} } \\[5px]
\end{align}
For the maximum possible force with which the water can be pushed upwards, a vacuum must be created inside the straw (p1=0), so that the entire ambient pressure p0 can push the water upwards inside the straw without counterpressure. In this case, the maximum suction lift hmax is obtained by creating a vacuum inside the straw:
\begin{align}
&h_{max} = \frac{p_0 – \overbrace{p_1}^{=0}}{\rho \cdot g} \\[5px]
&\boxed{h_{max} = \frac{p_0}{\rho \cdot g} }\\[5px]
\end{align}
At an ambient pressure of 1 bar, a liquid density of 1000 kg/m³ and a gravitational acceleration of 10 N/kg, the maximum suction lift is about 10 Meters for water:
\begin{align}
&\underline{h_{max}} = \frac{p_0}{\rho \cdot g} \approx \frac{10^5 \frac{\text{N}}{\text{m²}}}{1000 \frac{\text{kg}}{\text{m³}} \cdot 10 \frac{\text{N}}{\text{kg}}} = \underline{10 \text{ m}} \\[5px]
\end{align}
For this reason, the maximum drinking height is 10 metres. With a longer drinking straw, the ambient pressure can no longer push the water column upwards. The water column would simply stop at this height.
Note that the generation of a vacuum is only theoretical. Because with decreasing pressure, the boiling point of liquids also decreases. If the pressure becomes too low at some point, the liquid in the straw begins to vaporize and the gaseous molecules build up a pressure themselves (vapour pressure). At a temperature of 20 °C, for example, water will vaporize at a pressure of 23 mbar. The lowest pressure that can be achieved in static equilibrium with water at 20 °C is therefore 23 mbar and not vacuum. In practice, therefore, lower maximum suction lifts will be achieved than are theoretically possible with a vacuum.
Influence of immersion depth
It has already been mentioned that the immersion depth of the straw or the hoses of suction pumps has no influence on the maximum suction lift. This will be shown mathematically in the following. For this purpose, the entire water column inside the straw, which is pushed upwards, is considered. The force with which this water column is effectively pushed upwards again results from the difference between the forces at the lower and upper end of the water column:
\begin{align}
&F_p = F_2 – F_1 \\[5px]
&F_p = p_2 \cdot A – p_1 \cdot A \\[5px]
\label{f}
&F_p = \left(p_2 – p_1 \right) \cdot A \\[5px]
\end{align}
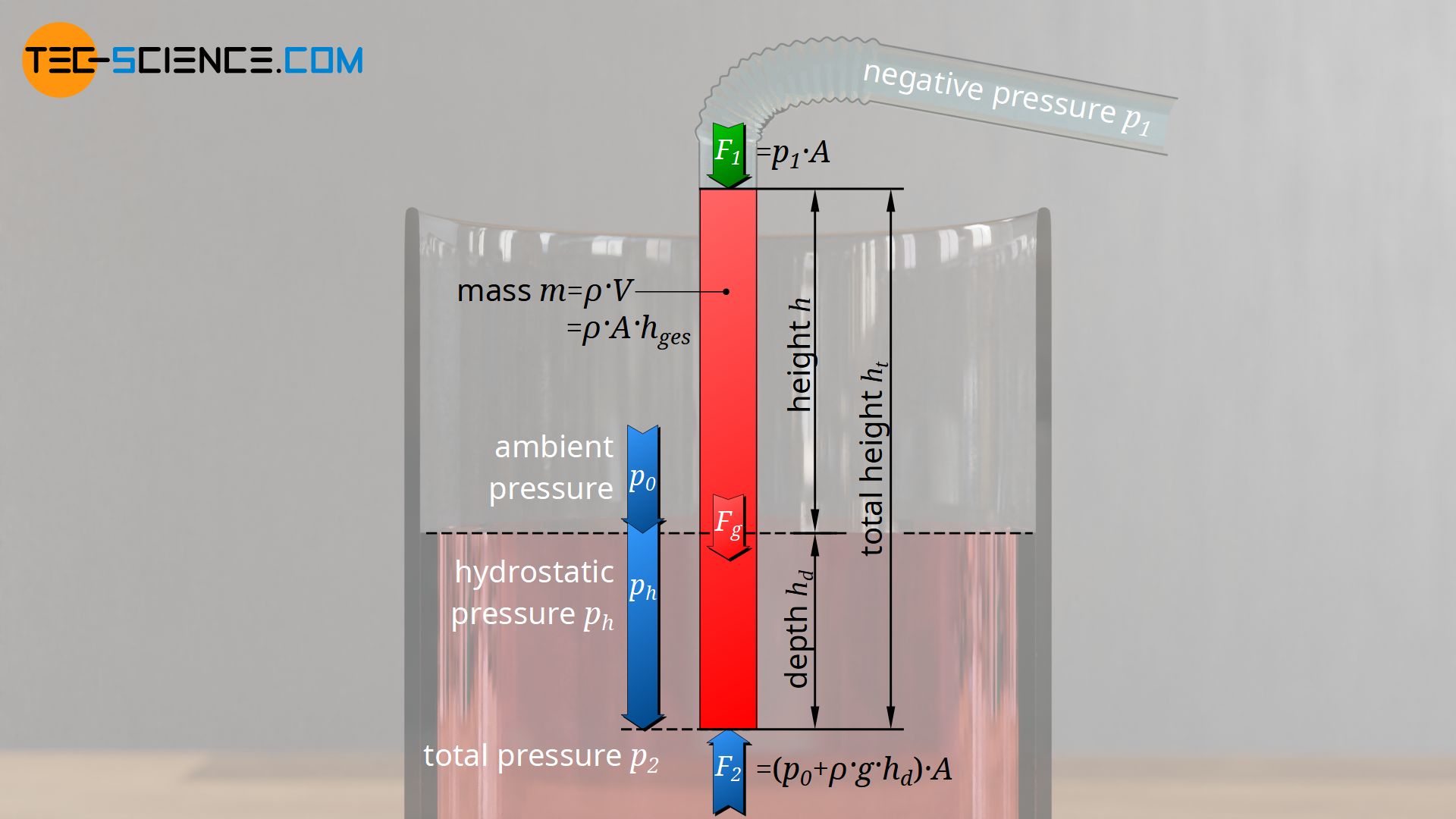
The pressure p2 acting at the lower end of the drinking straw results from the sum of ambient pressure p0 and hydrostatic pressure ph (see article Pressure in liquids). The hydrostatic pressure is determined by the density of the liquid ϱ, the gravitational acceleration g and the depth below the water surface hd. This depth hd corresponds to the immersion depth of the drinking straw.
\begin{align}
&p_2 = p_0 + p_h \\[5px]
\label{p}
&p_2 = p_0 + \rho g h_d \\[5px]
\end{align}
If equation (\ref{p}) is used in equation (\ref{f}), we obtain for the upwards acting force Fp:
\begin{align}
&F_p = \left(p_2 – p_1 \right) \cdot A \\[5px]
&\underline{F_p = \left(p_0 + \rho g h_d – p_1 \right) \cdot A} \\[5px]
\end{align}
This force Fp must again be large enough to push the water column with the weight Fg=m⋅g upwards. The total height ht of the water column inside the straw results from the immersion depth below the water surface dh and the water level above the water surface h. The weight of this water column can be determined by the cross-sectional area A and the liquid density ϱ:
\begin{align}
&F_g = m \cdot g ~~~~~\text{mit} ~~~ m = \rho \cdot V = \rho \cdot A \cdot h_{t} = \rho \cdot A \cdot (h_d+h) \\[5px]
&F_g = \rho g \left(h_d+h \right) \cdot A \\[5px]
&\underline{F_g = \left(\rho g h_d+ \rho g h\right) \cdot A} \\[5px]
\end{align}
In the state of equilibrium, the downwards acting weight Fg must be equal in magnitude to the upwards acting force Fp. The resulting suction lift h is determined as follows:
\begin{align}
\require{cancel}
F_p &\overset{!}{=} F_g \\[5px]
\left(p_0 + \rho g h_d – p_1 \right) \cdot \bcancel{A} & = \left(\rho g h_d+ \rho g h\right) \cdot \bcancel{A} \\[5px]
p_0 + \bcancel{\rho g h_d} – p_1 &= \bcancel{\rho g h_d}+ \rho g h \\[5px]
p_0 – p_1 &= \rho h g \\[5px]
\end{align}
\begin{align}
&\underline{h = \frac{p_0 – p_1}{\rho g} } \\[5px]
\end{align}
Even taking into account the immersion depth and the hydrostatic pressure acting there, the same formula is obtained, so that the suction lift is actually not dependent on the immersion depth itself!
There is also a clear explanation for this, because due to the hydrostatic pressure, the water in the open straw is pushed to a uniform level anyway. In accordance with the principle of communicating vessels, the water level inside the straw will be the same as outside. In this respect, the ambient pressure does not have to push the water inside the straw up to the surrounding water level – the hydrostatic pressure does this automatically. The ambient pressure is therefore only responsible for pushing the water up from the surrounding water level. The maximum suction lift therefore always refers to the water surface!






