Bei der Verformung von Einkristallen bilden sich Gleitstufen vorzugsweise unter 45° zur Zugachse, da dabei die Schubspannungen maximal sind.
Einleitung
Zeichnet sich eine Werkstoff auf atomarer Ebene durch einen einheitliche Gitterausrichtung aus (keine Korngrenzen), so spricht man auch von einem sogenannten Einkristall.
Wird ein solcher Einkristall unter Zug verformt, so zeichnen sich bei entsprechender Kristallausrichtung im Verformungsbereich schräg verlaufende Ringe ab. Dies ist anhand des abgebildeten Kupfer-Einkristalls sehr deutlich zu sehen. Es handelt sich bei diesen Ringen um sogenannte Gleitstufen.

Weshalb sich diese dabei bevorzugt unter einem Winkel von 45° abzeichnen, soll im Folgenden geklärt werden.
Scherkraft
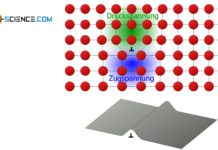
Der Einkristall mit einer Querschnittsfläche A0 wird äußerlich mit der Zugkraft F0 belastet. Um den Verformungsprozess in Gang zu setzen und ein Abscheren der Atomebenen zu ermöglichen, muss im Inneren eine Schubkraft F|| parallel zu den Gleitebenen wirken. Nur auf diese Weise kann die Ebene auch tatsächlich in Gleitrichtung verschoben werden. Eine senkrecht zu den Gleitebenen wirkende Normalkraft hat hingegen keinen Einfluss auf die Verformung. Die Ebenen würden hierdurch lediglich zusammengepresst aber nicht verschoben werden.
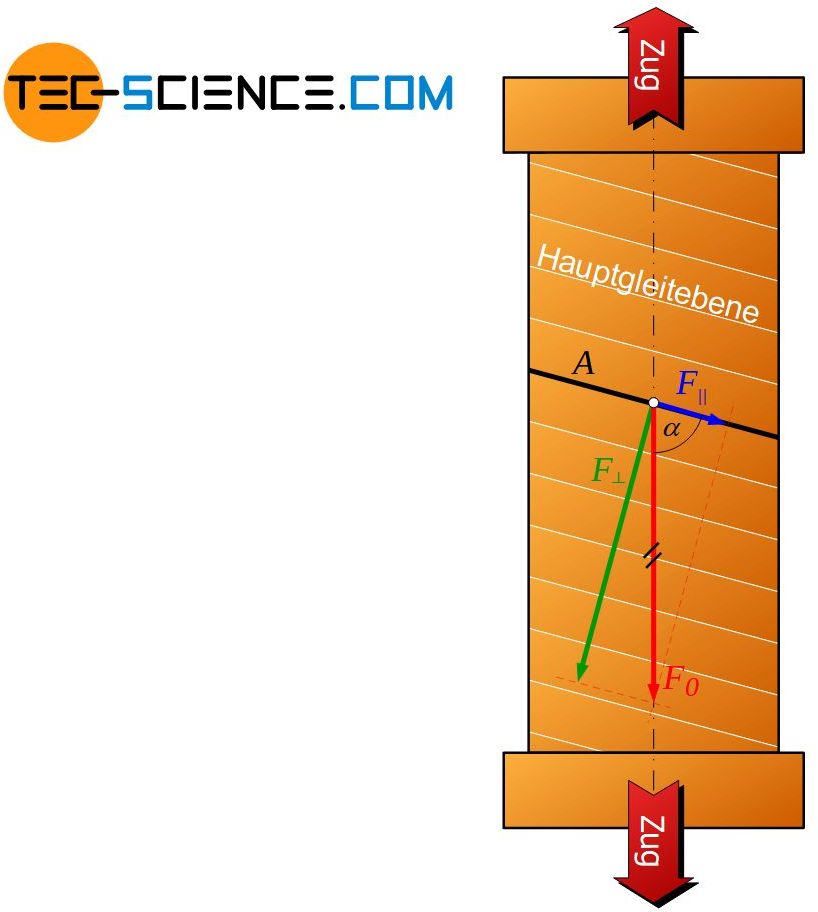
Liegt eine Gleitebene nun unter einem Winkel \(\alpha\) zur Zugachse, so kann durch eine Kräftezerlegung die äußere Kraft F0 in eine parallele Komponente (Scherkraft F||) und eine senkrechte Komponente (Normalkraft F⊥) zur Gleitebene zerlegt werden. Mathematisch lässt sich die Scherkraft und die Normalkraft in Abhängigkeit des Winkels \(\alpha\) wie folgt ermitteln:
\begin{align}
\label{kraft}
F_{\parallel}&=F_0 \cdot \cos(\alpha) ~~~~~\text{Schubkraft} \\[5px]
F_{\perp}&=F_0 \cdot \sin(\alpha)~~~~~\text{Normalkraft} \\[5px]
\end{align}
Ist der Winkel \(\alpha\) zwischen Flächennormalen und Zugachse relativ gering, so ist auch die Scherkraft in der Gleitebene relativ gering. Die Kraft reicht unter Umständen nicht aus, um die Gleitebene zu aktivieren und den Verformungsprozess in Gang zu setzen.
Liegt die Gleitebene hingegen unter einem relativ großen Winkel \(\alpha\) zur Zugachse, so ist zunächst zwar die Schubkraft in der Gleitebene relativ groß. Jedoch steigt gleichzeitig die Gleitebenenfläche und mit ihr die Bindungskraft zwischen den Ebenen. Auch in diesem Fall reicht unter Umständen die größere Schubkraft dennoch nicht aus, um die Ebene zum Abscheren zu bringen und den Verformungsprozess in Gang zu setzen.
Die Situation kann mit einem Klettverschluss verglichen werden, wobei die gegenseitigen Verhakungen zwischen den Verschlussmaterialien den Bindungen zwischen den Atomebenen entsprechen. Sind die Schubkräfte zum Öffnen des Klettverschlusses zu gering, so gleiten die Verschlussmaterialien nicht aufeinander ab. Jedoch führt eine Vervielfachung der Kraft auch dann nicht zum Abgleiten wenn gleichzeitig der Überlappungsbereich der beiden Verschlussmaterialien überproportional ansteigt.
Es muss demnach ein günstiges Verhältnis von Kraft und Fläche vorliegen, um den optimalen Zustand zu erreichen bei dem die meiste Kraft pro Fläche zu verzeichnen ist, d.h. die größte Schubspannung erzielt wird.
Schubspannung
Maßgebend für ein Abgleiten der Atomebenen ist demnach nicht die Kraft in der Gleitebene alleine sondern die wirkende Kraft pro Fläche, d.h. die Schubspannung (siehe hierzu auch Grundlagen der Verformung):
\begin{equation}
\label{schubspannung}
\tau=\frac{F_{\parallel}}{A}
\end{equation}
Während die Schubkraft F|| gemäß Gleichung (\ref{kraft}) von der Winkelstellung \(\alpha\) der Gleitebene abhängt, bestimmt sich die Gleitebenenfläche A wie folgt über den Probenquerschnitt A0:
\begin{equation}
\label{flaeche}
A=\frac{A_0}{\sin(\alpha)}
\end{equation}
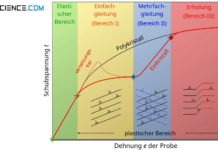
Die Zunahme der Schubkraft (blaue Kurve) und die Zunahme der Fläche (schwarze Kurve) mit geringer werdendem Winkel zeigt schematisch das unten abgebildete Diagramm. Zusätzlich ist der resultierende Verlauf der Schubspannung gezeigt (rote Kurve). Offensichtlich wirkt die größer Kraft pro Fläche unter einem Winkel von 45° zur Zugachse. Dies soll im folgenden Abschnitt auch mathematisch gezeigt werden.
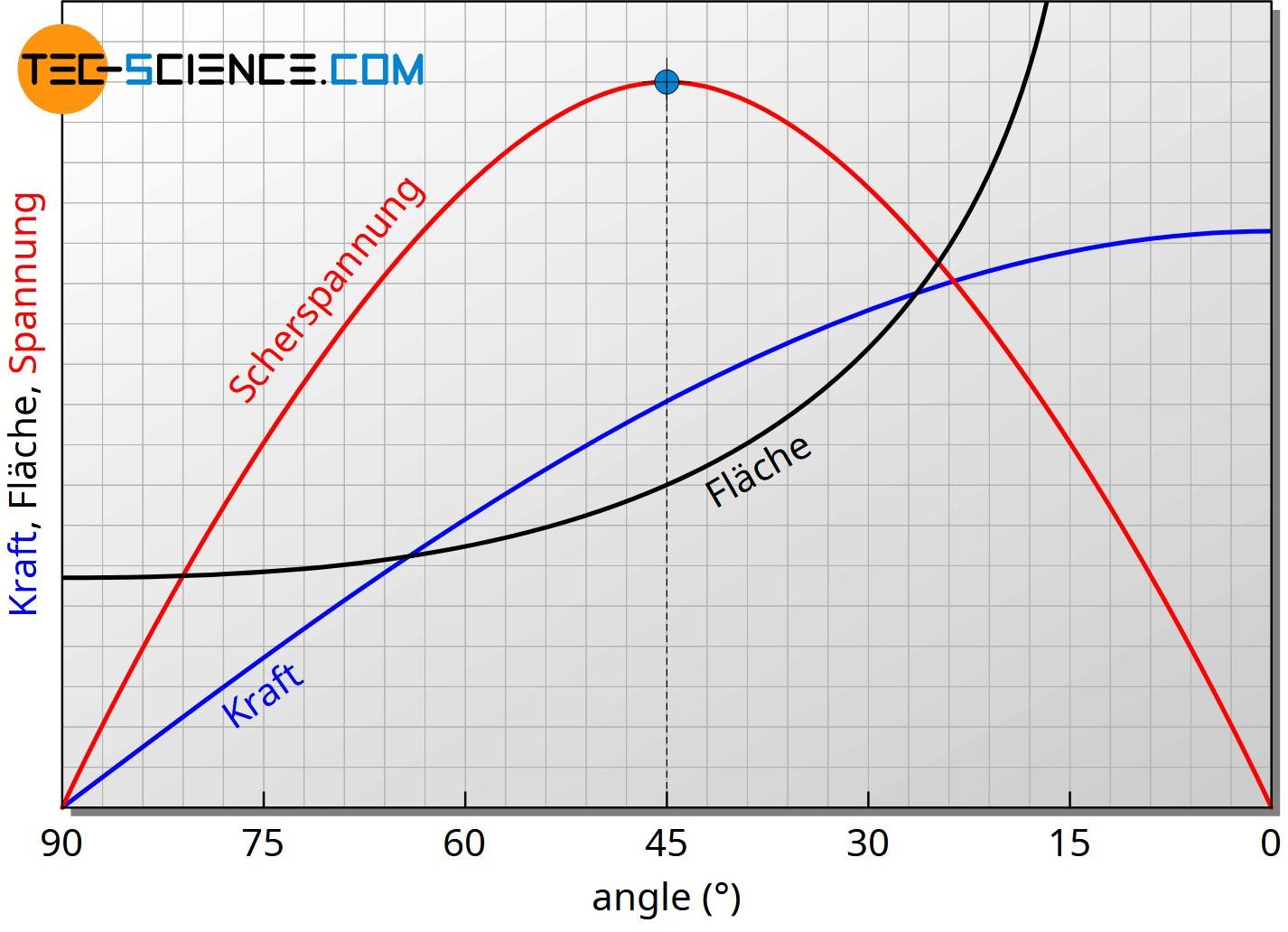
Maximale Schubspannung
Den gezeigten Verlauf der Scherspannung erhält man indem man die Gleichung (\ref{kraft}) für der Scherkraft und die Gleichung (\ref{flaeche}) für die Scherfläche in die Scherspannungsformel (\ref{schubspannung}) einsetzt:
\begin{equation}
\label{scherspannung}
\tau=\frac{F_{\parallel}}{A}=\frac{F_0 \cdot \cos(\alpha)}{\frac{A_0}{\sin(\alpha)}} =\frac{F_0}{A_0} \cdot \cos(\alpha) \cdot \sin(\alpha)
\end{equation}
Der in der Gleichung (\ref{scherspannung}) auftauchende Quotient \(\frac{F_0}{A_0}\) entspricht dabei gerade der von außen aufgebrachten Normalspannung \(\sigma_0\) („Kraft pro Querschnittsfläche“). Für die winkelabhängige Schubspannung \(\tau(\alpha)\) gilt daher:
\begin{equation}
\tau(\alpha)=\sigma_0 \cdot \cos(\alpha) \cdot \sin(\alpha)
\end{equation}
Ferner kann ausgenutzt werden, dass der Term \(\cos(\alpha) \cdot \sin(\alpha)\) durch den Ausdruck \(\frac{\sin(2\alpha)}{2}\) ersetzt werden kann. Somit gilt für die wirksame Schubspannung \(\tau\) in einer mit dem Winkel \(\alpha\) zur Zugachse liegenden Gleitebene:
\begin{equation}
\label{tau}
\boxed{\tau(\alpha)={\frac{\sin(2 \alpha)}{2} \cdot \sigma_0} }
\end{equation}
Die innere Schubspannung \(\tau\) hängt also von der anliegenden äußeren Spannung \(\sigma_0\) und in besonderem Maße von der Winkelstellung \(\alpha\) ab. Der Term \(\sin(2\alpha)\) erreicht dabei für einen Winkel von \(\alpha\)=45° den Maximalwert 1.
Es zeigt sich nun auch auf mathematischen Wege, dass die maximale Schubspannung \(\tau_{max}\) folglich bei einem Winkel von \(\alpha\)=45° erreicht wird. Für diesen Fall entspricht die maximale Schubspannung genau der Hälfte der äußeren Normalspannungen \(\sigma_0\)!
\begin{equation}
\label{max}
\boxed{\tau_{max}=\frac{\sigma_0}{2}} ~~~ \text{für} ~~~ \alpha=45°
\end{equation}
Äußere Normalspannungen induzieren im Werkstoffinneren Schubspannungen, die unter einem Winkel von 45° maximal werden. In jenen günstig gelegenen Gleitebenen scheren die Atomschichten deshalb bevorzugt ab!
Dies ist der Grund weshalb der oben gezeigte Kupfer-Einkristall Gleitstufen unter einem Winkel von ca. 45° zur Zugachse aufweist. Voraussetzung hierfür ist, dass die Gitterstruktur räumlich so orientiert ist, dass sich eine Gleitebene möglichst unter einem Winkel von 45° ergibt. Welche Auswirkungen sich auf den Verformungsprozess ergeben, wenn die Gleitebene nicht unter einem Winkel von 45° liegt, wird im nächsten Abschnitt diskutiert.
Anmerkung: Neben der optimalen Orientierung der Gleitebene muss zudem auch die Gleitrichtung entsprechend orientiert sein. Von dieser optimalen Orientierung wurde bisher stillschweigend ausgegangen. Im Beitrag Schmid’sches Schubspannungsgesetz wird hierauf näher eingegangen.
Einfluss der Gitterorientierung
Wie sieht nun die Verformung eines Einkristalls aus, wenn dessen Gleitebenen nicht unter einem Winkel von 45° liegen? Aufgrund der ungünstigeren Lage sind in diesem Fall zunächst größere äußere Normalspannungen erforderlich damit die kritischen Schubspannung in der Gleitebene (und in Gleitrichtung!) überschreiten werden.
Mehrfachgleitung
Bei sehr ungünstiger Lage der (Haupt-)Gleitebenen kann dies dann sogar dazu führen, dass andere Gleitebenen aktiviert werden welche normalerweise erst bei größeren Spannungen zum Zuge kommen, da in diesen zuerst die kritische Schubspannung überschritten wird. Eventuell finden auch in mehreren unterschiedlichen Gleitsystemen Abgleitvorgänge statt.
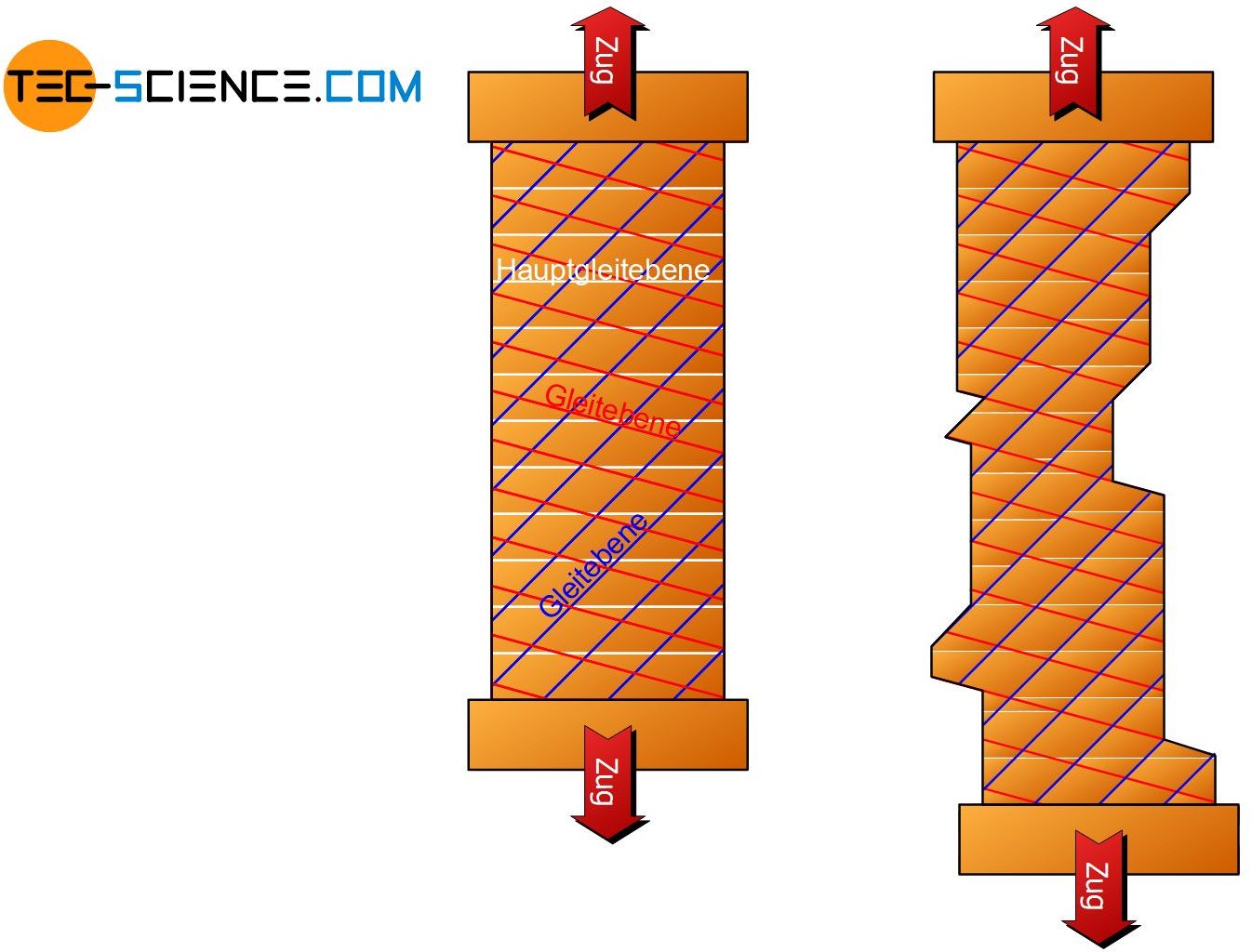
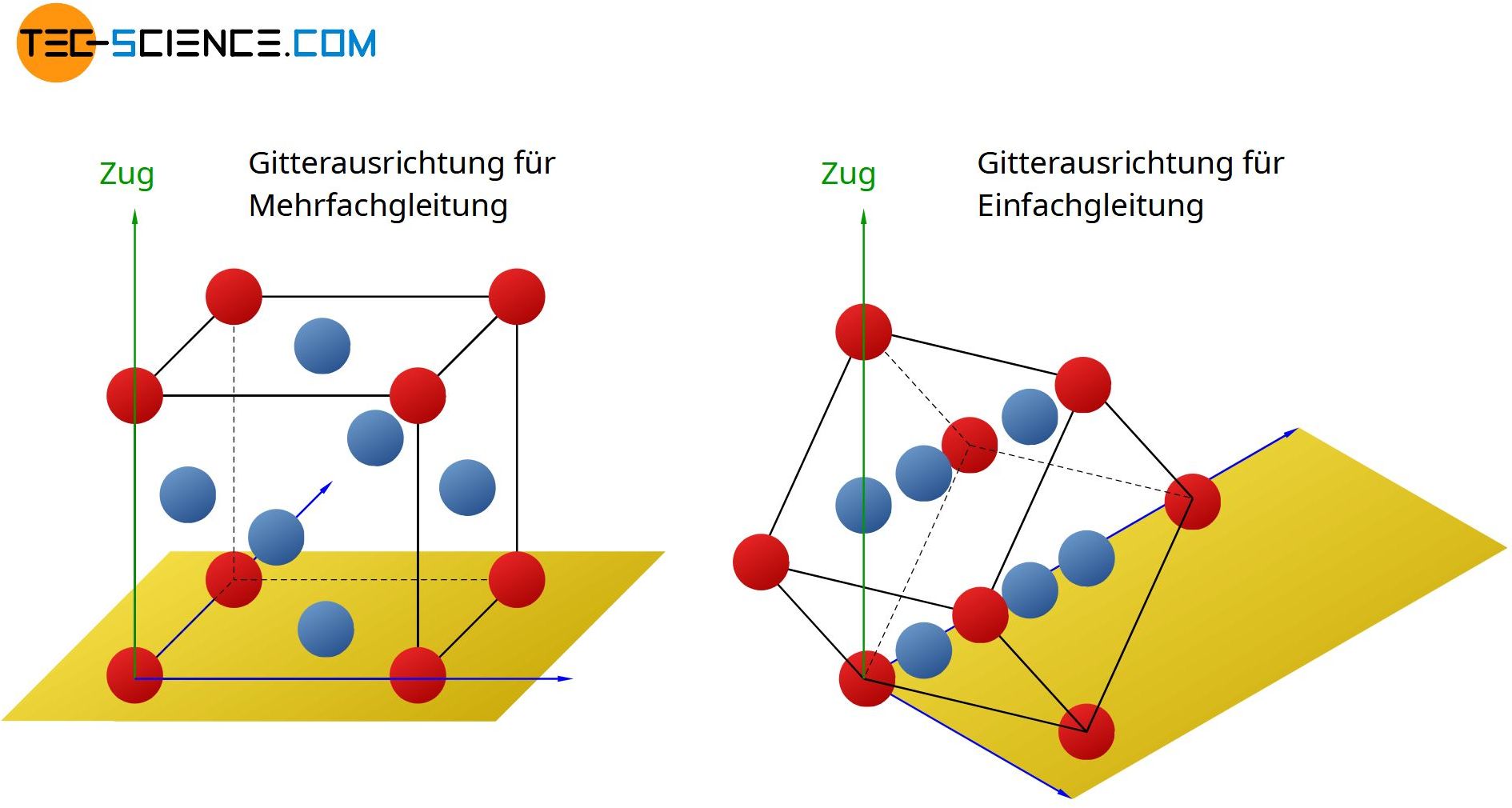
Dies wird der Fall sein, wenn die unterschiedlichen Gleitebenen relativ symmetrisch zur Zugachse liegen. Dann wird die kritische Schubspannung in allen ungefähr gleichzeitig erreicht. Bei kubisch-flächenzentrierten Einkristallen müssen die Elementarzellen hierfür nahezu parallel zur Zugachse ausgerichtet sein (siehe Abbildung unten „Gitterorientierung für Einfach- und Mehrfachgleitung“).
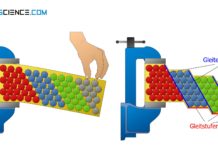
Alle vier Gleitebenen werden dann gleichermaßen aktiviert. Aufgrund der Tatsache, dass das Abscheren auf mehreren unterschiedlichen Gleitebenen stattfindet, spricht man auch von Mehrfachgleitung. Bei einer solchen Mehrfachgleitung wird der Kristall dann in unterschiedliche Richtungen verformt.
Einfachgleitung
Je nach Orientierung der Gleitebenen treten die Gleitstufen unter unterschiedlichen Winkeln und räumlichen Richtungen aus und sind nicht mehr so deutlich sichtbar. In der Abbildung des Kupfer-Einkristalls war das kfz-Kristallgitter hingegen speziell zur Zugachse ausgerichtet, sodass nur eine Gleitebene möglichst unter einem Winkel von rund 45° zur Zugachse orientiert war.
Somit wurde bei Erreichen der Grenzspannung auch nur diese Gleitebene aktiviert, während die Schubspannungen in den übrigen Gleitebenen (bzw. in Gleitrichtung) unterhalb der kritischen Schubspannung blieben. Da in einem solchen Fall das Abgleiten nur in einer Gleitebene stattfindet, bezeichnet man diesen Vorgang auch als Einfachgleitung.
Die von außen anzulegende Spannung \(\sigma_{krit}\) an einen Werkstoff, damit in einer günstig gelegenen Gleitebene die kritische Schubspannung überschritten wird und es zum Abgleiten kommt, wird auch Fließgrenze, Dehngrenze oder Elastizitätsgrenze genannt.
Dieser Wert bezeichnet somit die äußere Grenz(zug)spannung, ab der ein irreversibler Verformungsprozess in einem Material einsetzt. Wie erläutert, hängt diese Fließgrenze bei Einkristallen von der räumlichen Orientierung des Gitters ab! Den geringsten Wert der Fließgrenze erhält man bei Einkristallen folglich wenn dessen Gleitebenen unter einem Winkel von 45° zur Zugachse verlaufen.
Die Fließgrenze kennzeichnet die äußere Grenzspannung ab der sich ein Werkstoff plastisch verformt!
Polykristalle
Das ringförmige Abzeichnen der Gleitstufen unter einem Winkel von 45° zeigt sich folglich lediglich bei speziell orientierten Einkristallen. Einkristalle sind allerdings nur unter hohem technischem Aufwand herstellbar. Sie bleiben deshalb auf Spezialanwendungen wie z.B. für das Herstellen von einkristallinen Turbinenschaufeln auf Nickelbasis oder der Silizium-Chipherstellung beschränkt.
In der Regel weisen Metalle keine einheitliche Gitterausrichtung auf (Achtung: der Begriff Gitterausrichtung darf nicht mit dem Begriff Gitterstruktur verwechselt werden!). Vielmehr finden sich in Metallen viele kleine mikroskopische Bereiche (Körner) mit jeweils unterschiedlicher Gitterausrichtung wieder (Polykristall genannt).
Somit werden auch stets mehrere Gleitsysteme mit unterschiedlicher Gleitebenenorientierung aktiviert (Mehrfachgleitung). Ein einheitliches Austreten der Gleitstufen aus dem Werkstoff wird deshalb bei solchen Werkstoffen ohnehin nicht sichtbar. Wie es zu einer solchen uneinheitlichen Gitterausrichtung kommt wird im Kapitel Gefügeentstehung näher erläutert.

In diesem Beitrag wurden lediglich die Prozesse besprochen, die zum Auslösen eines Verformungsvorgangs führen. Auf den eigentlichen Verformungsprozess in Einkristallen wird deshalb im Beitrag Verformungsprozess im Einkristall näher eingegangen.