Als Packungsdichte bezeichnet man das Verhältnis des Atomvolumens innerhalb einer Elementarzelle, zum Volumen der Elementarzelle.
Definition der Packungsdichte
Als Packungsdichte bezeichnet man das Verhältnis von Atomvolumen \(V_A\) innerhalb einer Elementarzelle zum Gesamtvolumen der Elementarzelle \(V_{EZ}\):
\begin{align}
\boxed{\text{PD}=\frac{V_A}{V_{EZ}} } \\[5px]
\end{align}
Je nach Gitterstruktur ergibt sich eine bestimmte Packungsdichte. Die Packungsdichten von den wichtigsten Gitterarten sollen im Folgenden ermittelt werden.
Kubisch-raumzentriertes Gitter
Um die Packungsdichte im kubisch-raumzentrieten Gitter zu ermitteln, wird die Raumdiagonale \(e\) der würfelförmigen Elementarzelle betrachtet. Die drei auf dieser Diagonalen liegenden Atomkugeln berühren sich gerade gegenseitig. Somit entspricht die Raumdiagonale dem 4-fachen Atomradius \(r\). In einem Würfel ist die Raumdiagonale um den Faktor √3 größer als die Würfelkante \(a\). Somit ergibt sich der Atomradius \(r\) in Abhängigkeit der Würfelkante \(a\) wie folgt:
\begin{align}
e=\sqrt{3} \cdot a = 4 \cdot r ~\Rightarrow ~ \underline{r= \frac{\sqrt{3}}{4} \cdot a}
\end{align}
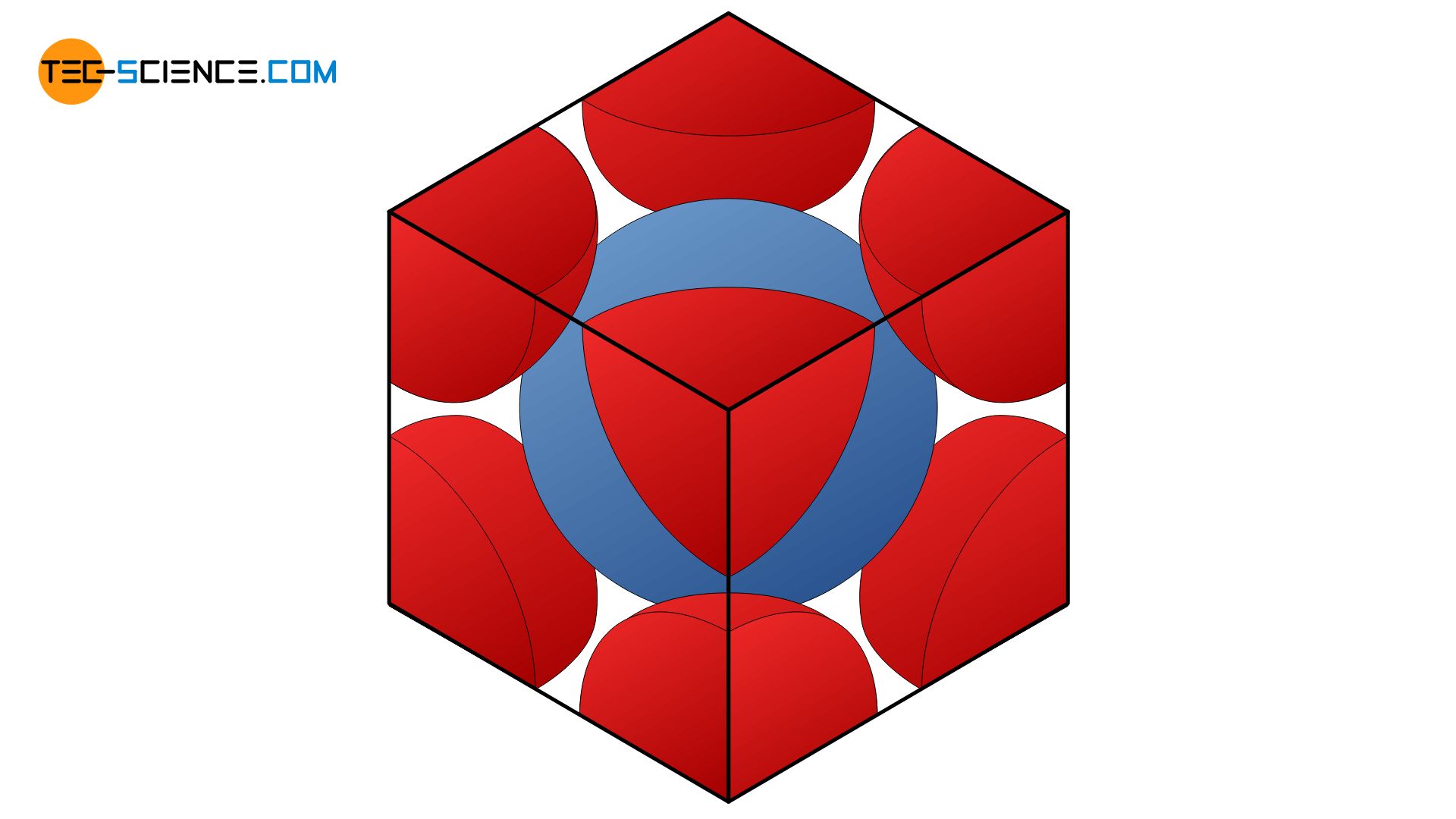
In der Elementarzelle befindet sich ein ganzes Atom in der Mitte und acht weitere zu je einem Achtel auf den Würfelecken. Insgesamt befindet sich also das Volumen von zwei vollen Atomkugeln in der Elementarzelle mit dem Atomvolumen \(V_A\):
\begin{align}
\underline{V_A} =2 \cdot V_{Kugel}
=2 \cdot \frac{4}{3} \pi \cdot r^3
=\frac{8}{3} \pi \cdot \left( \frac{\sqrt{3}}{4} \cdot a \right)^3
= \underline{ \frac{\sqrt{3}}{8} \pi \cdot a^3}
\end{align}
Dieses Atomvolumen \(V_A\) kann nun ins Verhältnis zum Elementarzellenvolumen \(V_{EZ}=a^3\) gesetzt werden, sodass für die Packungsdichte \(\text{PD}\) des kubisch-raumzentrierten Gitters gilt:
\begin{align}
\underline{\underline{\text{PD}}}= \frac{V_A}{V_{EZ}} =\frac{\frac{\sqrt{3}}{8} \pi \cdot a^3}{a^3}=\frac{\sqrt{3}}{8} \pi \approx \underline{\underline{0,68}}
\end{align}
Somit besitzt das krz-Gitter einen Atomvolumenanteil von 68 %.
Kubisch-flächenzentriertes und hexagonal dichtest gepacktes Gitter (kfz, hdp)
Die Packungsdichte im kubisch-flächenzentrierten Gitter (kfz) kann auf analoge Weise wie für die kubisch-raumzentrierte Struktur ermittelt werden. Dabei berühren sich drei Atomkugeln auf der Flächendiagonalen der Elementarzelle. Die Flächendiagonale \(f\) entspricht somit dem 4-fachen Atomradius, wobei die Flächendiagonale dem Wert √2·\(a\) entspricht (\(a\) ist die Würfelkante). Somit ergibt sich der Atomradius \(r\) in Abhängigkeit der Würfelkante wie folgt:
\begin{align}
f=\sqrt{2} \cdot a = 4 \cdot r ~\Rightarrow ~ \underline{r= \frac{\sqrt{2}}{4} \cdot a}
\end{align}
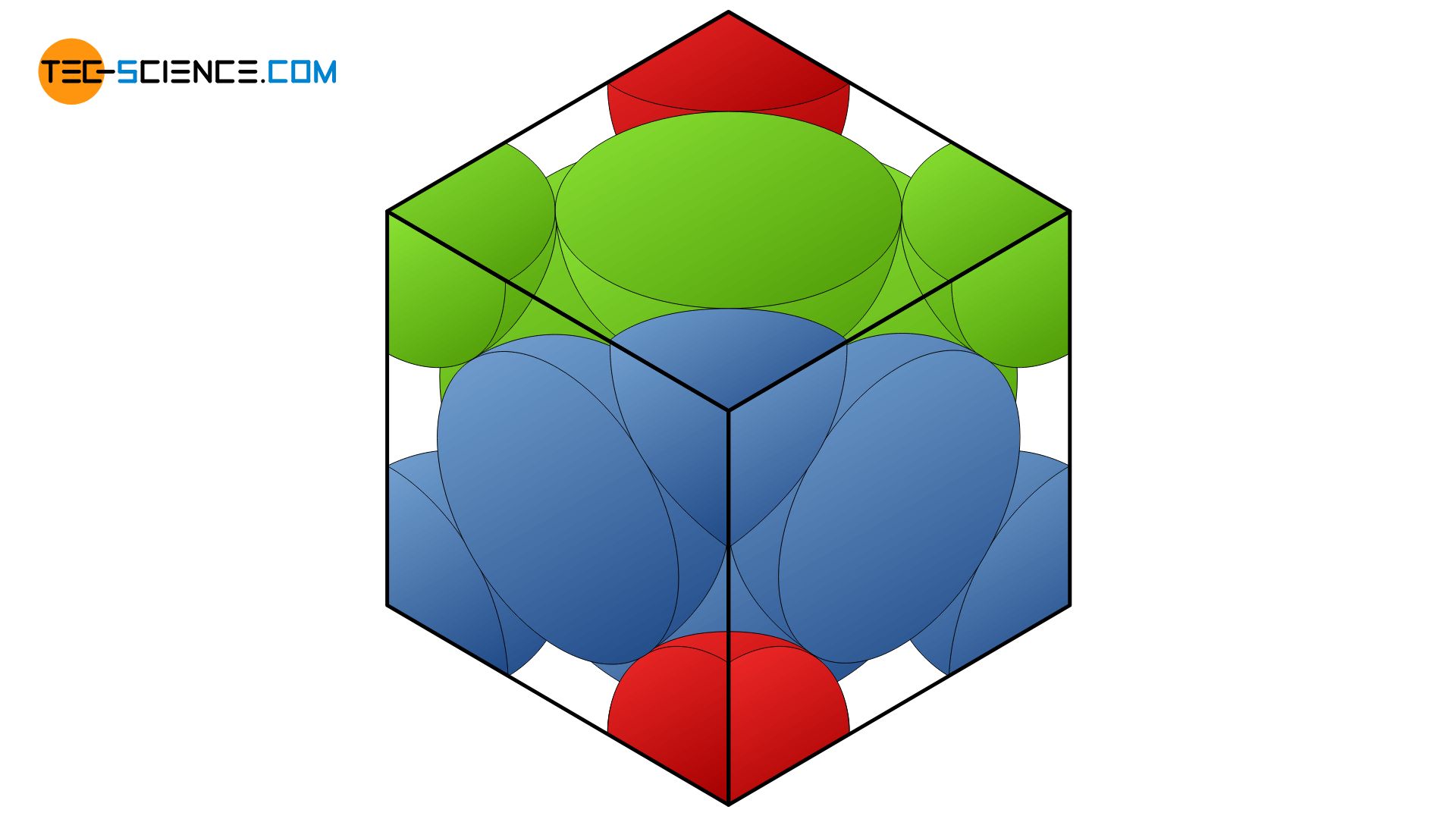
In der kfz-Elementarzelle befinden sich sechs Atome auf den Würfelflächen, deren Volumen sich je zur Hälfte in der Elementarzelle befindet (3 ganze Atomvolumina). Zusätzlich befinden sich acht weitere Atome zu je einem Achtel auf den Würfelecken (1 ganzes Atomvolumen). Insgesamt befindet sich also das Volumen von vier vollen Atomkugeln in der Elementarzelle mit dem Atomvolumen \(V_A\):
\begin{align}
\underline{V_A} =4 \cdot V_{Kugel}
=4 \cdot \frac{4}{3} \pi \cdot r^3
= \frac{16}{3} \pi \cdot \left( \frac{\sqrt{2}}{4} \cdot a \right)^3
= \underline{ \frac{\sqrt{2}}{6} \pi \cdot a^3}
\end{align}
Dieses Atomvolumen \(V_A\) kann nun ins Verhältnis zum Elementarzellenvolumen \(V_{EZ}=a^3\) gesetzt werden, sodass für die Packungsdichte \(\text{PD}\) des kubisch-flächenzentrierten Gitters gilt:
\begin{align}
\underline{\underline{\text{PD}}}= \frac{V_A}{V_{EZ}} =\frac{\frac{\sqrt{2}}{6} \pi \cdot a^3}{a^3}=\frac{\sqrt{2}}{6} \pi \approx \underline{\underline{0,74}}
\end{align}
Das kfz-Gitter weist somit einen Atomvolumenanteil von 74 % auf. Dabei muss gunrdsätzlich nicht zwischen dem kfz-Gitter und dem hexagonal-dichtestgepackten Gitter (hdp) unterschieden werden, da es sich in beiden Fällen jeweils um Stapelungen dichtestgepackter Ebenen handelt (siehe Beitrag Wichtige Gittertypen). Die Packungsdichte im hdp-Gitter besitzt somit ebenfalls den maximal möglichen Wert von 74 %.