The packing density is the ratio of the atomic volume within a unit cell to the volume of the unit cell.
Definition of the packing density
The packing density is the ratio of atomic volume \(V_A\) within a unit cell to the total volume of the unit cell \(V_{U}\):
\begin{align}
\boxed{\text{PD}=\frac{V_A}{V_{U}} } \\[5px]
\end{align}
Depending on the grid structure, there is a certain packing density. The packing factors of the most important lattice types are to be derived in this article.
Body-centered cubic lattice
In order to determine the packing density for the body-centered cubic crystalline structure, the spatial diagonal \(e\) of the cube-shaped unit cell is considered. The three atoms lying on this diagonal are just touching each other. Thus, the spatial diagonal corresponds to 4 times the atomic radius \(r\). In a cube, the spatial diagonal is larger by a factor √3 than the edge of the cube \(a\). Thus, the atomic radius \(r\) depending on the cube edge \(a\) as follows:
\begin{align}
e=\sqrt{3} \cdot a = 4 \cdot r ~\Rightarrow ~ \underline{r= \frac{\sqrt{3}}{4} \cdot a}
\end{align}
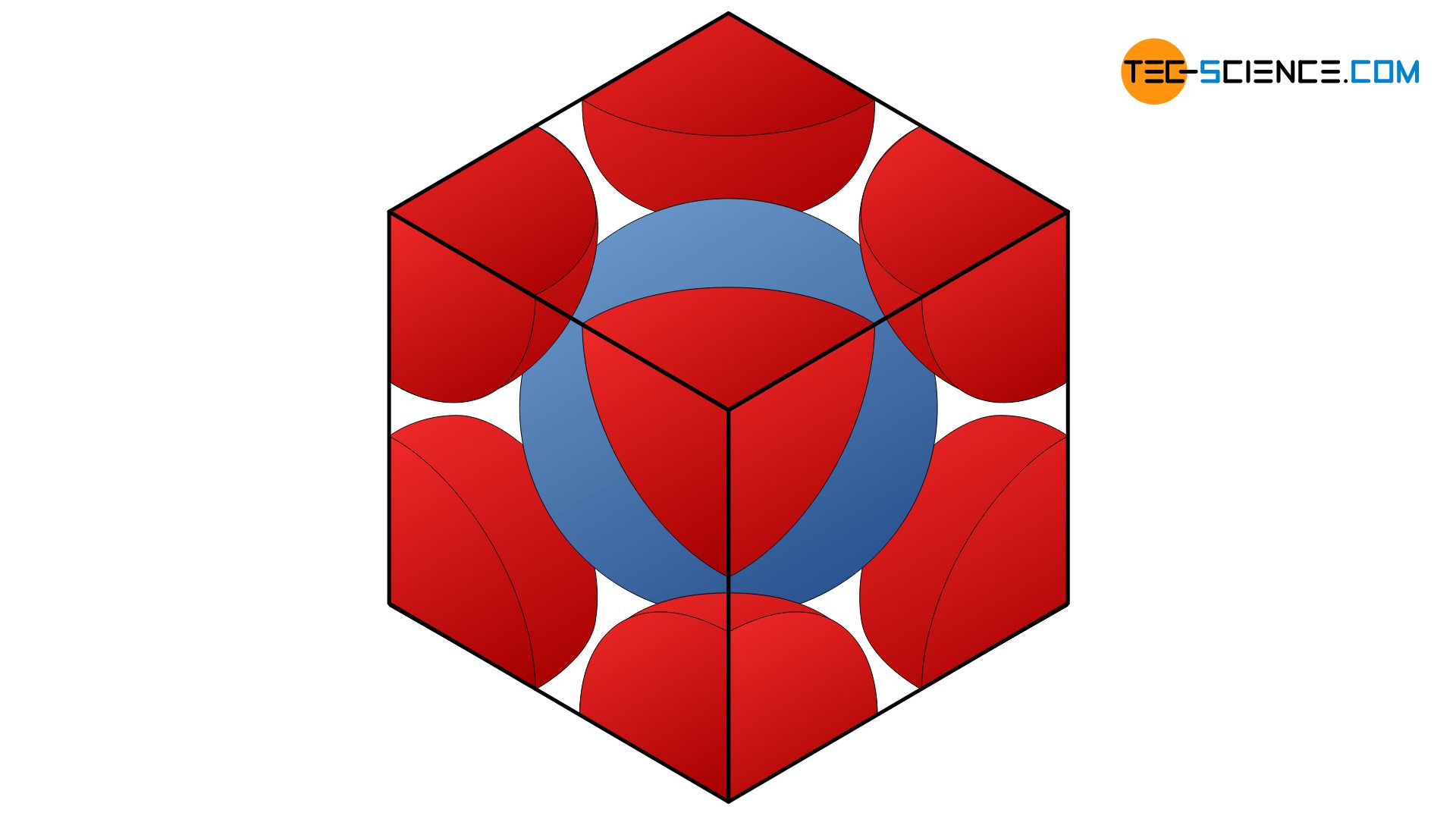
In the unit cell, there is a whole atom in the middle and eight others on the cube corner, but only with one eighth each. In total the volume \(V_A\) of two atomic spheres is in the unit cell:
\begin{align}
\underline{V_A} =2 \cdot V_{sphere}
=2 \cdot \frac{4}{3} \pi \cdot r^3
=\frac{8}{3} \pi \cdot \left( \frac{\sqrt{3}}{4} \cdot a \right)^3
= \underline{ \frac{\sqrt{3}}{8} \pi \cdot a^3}
\end{align}
This atomic volume \(V_A\) can now put into relation to the unit cell volume \(V_{U}=a^3\) in order to obtain the packing density \(\text{PD}\) of the body-centered cubic lattice:
\begin{align}
\underline{\underline{\text{PD}}}= \frac{V_A}{V_{U}} =\frac{\frac{\sqrt{3}}{8} \pi \cdot a^3}{a^3}=\frac{\sqrt{3}}{8} \pi \approx \underline{\underline{0,68}}
\end{align}
Thus, the bcc-lattice has a packing facotr of 68 %.
Face-centered cubic and hexagonal closest packed lattice (fcc, hcp)
The packing density of the face-centered cubic lattice (fcc) can be determined in an analogous manner as for thebody-centered cubic structure. Three atomic spheres touch each other on the surface diagonal of the unit cell. This diagonal \(f\) thus corresponds to 4 times the atomic radius and equals to the value \(\sqrt{2} \cdot a\) (where \(a\) is the cube edge). Thus, the atomic radius \(r\) depends on the cube edge as follows:
\begin{align}
f=\sqrt{2} \cdot a = 4 \cdot r ~\Rightarrow ~ \underline{r= \frac{\sqrt{2}}{4} \cdot a}
\end{align}
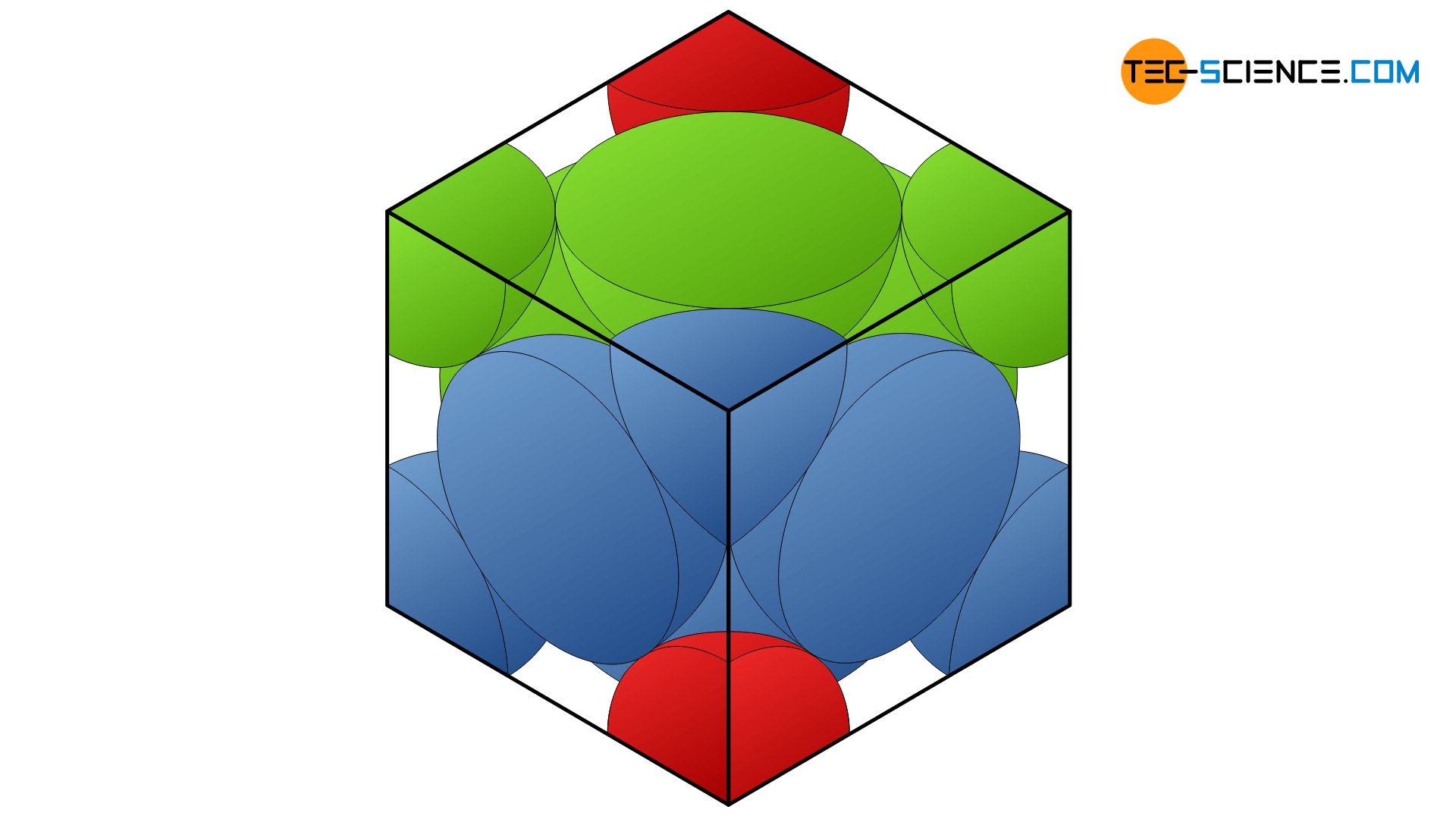
In the fcc unit cell, there are six atoms on the cube surfaces, but only with one half of their sphere volume (in total 3 whole atomic volumes). In addition, there are eight other atoms on the cube corner, but only with one eighth each (1 whole atomic volume). In total the volume of four atomic spheres is in the unit cell with the atomic volume \(V_A\):
\begin{align}
\underline{V_A} =4 \cdot V_{sphere}
=4 \cdot \frac{4}{3} \pi \cdot r^3
= \frac{16}{3} \pi \cdot \left( \frac{\sqrt{2}}{4} \cdot a \right)^3
= \underline{ \frac{\sqrt{2}}{6} \pi \cdot a^3}
\end{align}
This atomic volume \(V_A\) can now put into relation to the unit cell volume \(V_{U}=a^3\). The packing density \(\text{PD}\) of the face-centered cubic grid is calculated as follows:
\begin{align}
\underline{\underline{\text{PD}}}= \frac{V_A}{V_{U}} =\frac{\frac{\sqrt{2}}{6} \pi \cdot a^3}{a^3}=\frac{\sqrt{2}}{6} \pi \approx \underline{\underline{0,74}}
\end{align}
The fcc-lattice thus has an packing factor of 74 %. However, there is no need to differentiate between the fcc-structure and the hexagonal closest packed crystal (hcp), since in both cases they built up by densest packed atomic planes (for further information see post on Important lattice types). The packing density in the hcp-lattice thus also has the maximum possible value of 74 %.