Durch das Saugen wird im Trinkhalm ein Unterdruck erzeugt, sodass der größere Umgebungsdruck, das Getränk durch den Trinkhalm drückt.
Einleitung
Das Trinken aus einem Strohalm klingt zunächst recht einfach. Ein Ende des Halms wird in ein wassergefülltes Glas gestellt und am anderen Ende wird die Flüssigkeit in den Mund gesogen. Man könnte nun meinen, dass ein solcher Trinkhalm prinzipiell beliebig lang sein könnte – um beliebig große Höhenunterschiede zu überwinden, müsste man nur kräftig genug daran saugen. Die Praxis zeigt aber, dass mit zunehmender Höhe es immer schwieriger wird die Flüssigkeit durch den Halm zu befördern. Ab einer Höher von ca. 10 Metern wird es schließlich überhaupt nicht mehr möglich sein, aus einem solchen Trinkhalm Wasser zu trinken. Auch die stärkste Vakuumpumpe der Welt könnte in diesem Fall kein Wasser mehr noch oben pumpen!
Tatsächlich ist nämlich nicht das Erzeugen des Unterdrucks beim Ansaugen die begrenzende Größe sondern der Umgebungsdruck! Ohne den Umgebungsdruck wäre es prinzipiell nicht möglich aus einem Strohalm zu trinken (dies gilt auch für Saugpumpen). Das Prinzip des Trinkens mit einem Strohalm bzw. die Arbeitsweise von Saugpumpen und die damit verbundene, limitierte Förderhöhe, sollen in diesem Artikel näher erläutert werden.

Funktionsprinzip
Zunächst stelle man sich ein Gefäß mit Wasser vor. Im Glas befindet sich ein runde Scheibe, die direkt auf der Wasseroberfläche aufliegt. In der Mitte der Scheibe ist ein Loch eingebracht durch das ein Trinkhalm ins Wasser geführt wird. Wird die Scheibe nun nach unten gedrückt, dann wird das Wasser durch den Strohhalm nach oben gepresst.

Auf prinzipiell dieselbe Weise ist auch der auf der Wasseroberfläche lastende Umgebungsdruck in der Lage das Wasser durch den Trinkhalm nach oben zu drücken. Wird der Strohhalm jedoch einfach nur ins Wasser gestellt, dann ist die Kraft mit der der äußere Umgebungsdruck versucht das Wasser nach oben zu drücken (wie im Beispiel oben mit der Scheibe) genauso groß wie die Kraft mit der der innere Umgebungsdruck im Trinkhalminneren das Wasser nach unten drückt.
Soll das Wasser effektiv nach oben gefördert werden, dann muss der Luftdruck im Inneren des Strohhalms gegenüber dem äußeren Luftdruck gesenkt werden. Hierdurch wird eine geringere Gegenkraft erzeugt, sodass die Kraft des äußeren Umgebungsdruck in der Lage ist das Wasser nach oben zu drücken. Das Absenken des inneren Druckes im Trinkhalm geschieht durch Saugen an dessen Öffnung, sodass die darin befindlichen Luftteilchen abgesaugt werden. Hierdurch kommt es zu einem Unterdruck im Halm. Auf diese Weise wird das Wasser durch den größeren äußeren Umgebungsdruck entgegen des geringeren Druckes im Inneren des Trinkhalms nach oben gedrückt.
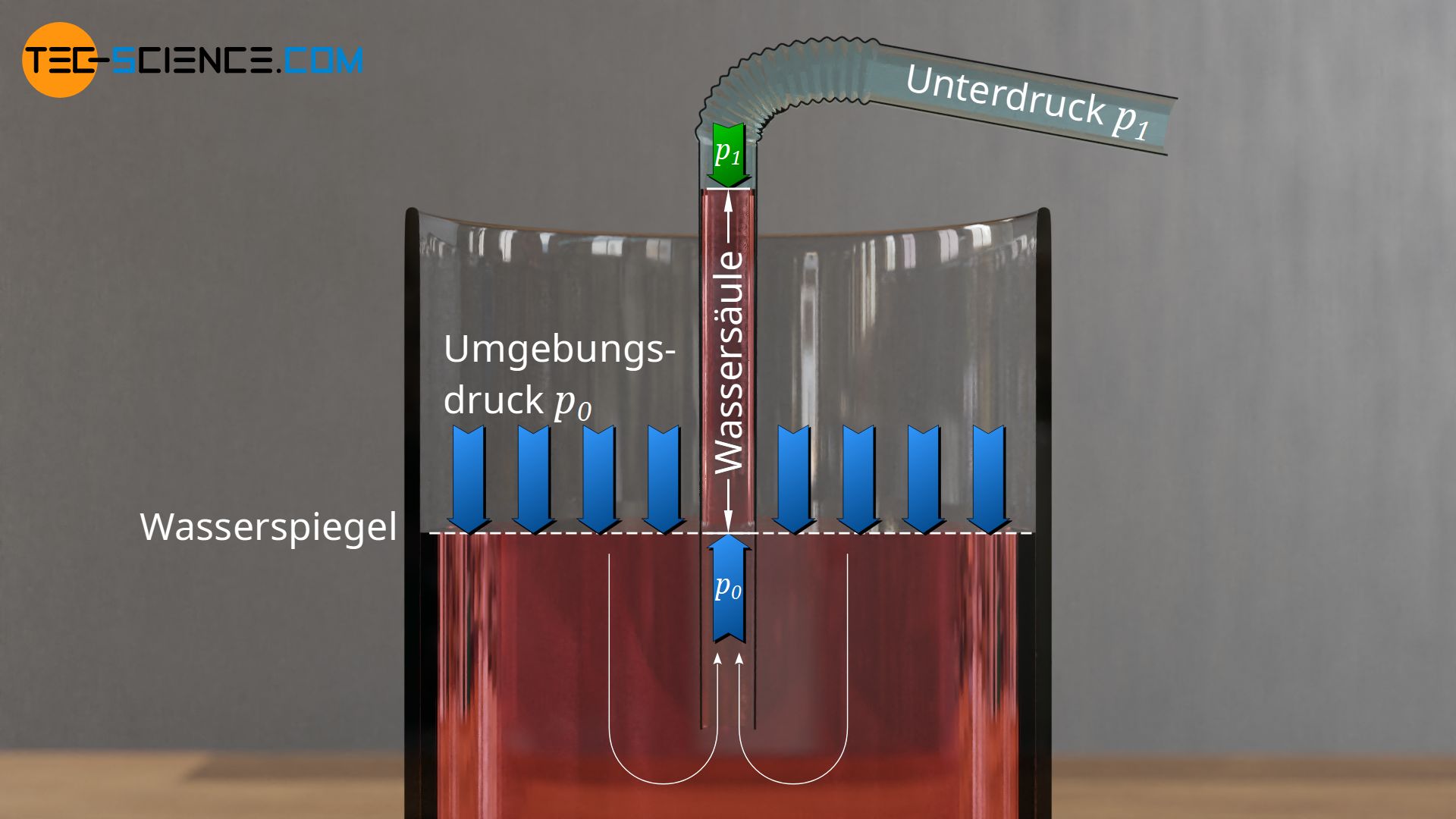
Es ist also der umgebende Luftdruck der es erst ermöglicht, dass das Wasser im Trinkhalm nach oben gedrückt werden kann. Das Erzeugen des Unterdrucks im Trinkhalm ist sozusagen lediglich Mittel zum Zweck. Würde hingegen kein Umgebungsdruck existieren (Vakuum), so könnte das Wasser auch nicht mehr durch irgendwelche Luftteilchen nach oben gedrückt werden. Aus diesem Grund ist es auch im freien Weltall nicht möglich ein Glas Wasser mit Hilfe eines Strohhalms zu trinken (von der Tatsache einmal abgesehen, dass Wasser aufgrund des Vakuums ohnehin sofort gasförmig werden würde)!
Maximale geodätische Saughöhe
Wie im einleitenden Abschnitt bereits erwähnt, wird man ab einer bestimmten zu überbrückenden Höhendifferenz zwischen Wasseroberfläche und Mund feststellen, dass es selbst unter einer noch so großen Anstrengung nicht mehr möglich ist aus dem Trinkhalm zu trinken. Dies Grenze liegt für Wasser theoretisch bei rund 10 m. Dies hat nicht etwa mit einer zu schwach ausgeprägten Mundmuskulatur zu tun sondern hat eine natürliche physikalische Ursache. So würde auch selbst die stärkste Saugpumpe der Welt bei Erzeugung eines perfekten Vakuums nicht mehr als 10 Metern Höhendifferenz überwinden können. Diese maximale geodätische Saughöhe soll im Folgenden mathematisch hergeleitet werden.
Die Kraft Fp mit der das Wasser effektiv nach oben gedrückt werden kann, ergibt sich aus der Differenz der Kräfte, die am unteren Ende (F0) und oberen Ende der Wassersäule (F1) wirken. Als Wassersäule ist dabei das Wasser im Halm bezogen auf den Wasserspiegel im Glas zu verstehen. Auf dieser Höhe wirkt auch selbst im Wasser der Umgebungsdruck p0 (da an dieser Stelle kein hydrostatischer Druck vorhanden ist), sodass dieser direkt dafür verantwortlich ist, dass das Wasser nach oben gedrückt wird. Die Eintauchtiefe des Trinkhalms spielt dabei keine Rolle (später mehr dazu).
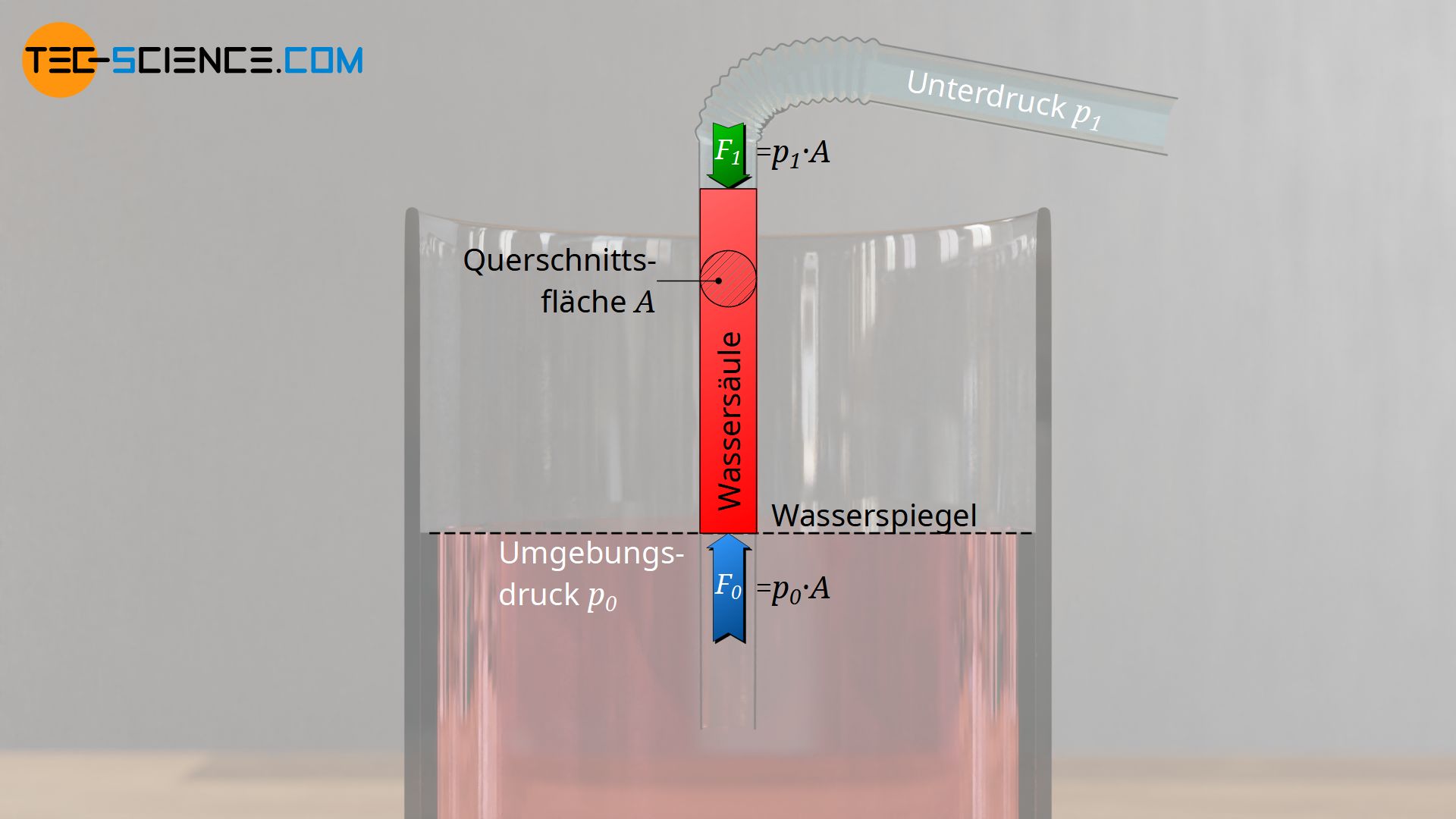
Die effektiv nach oben wirkende Kraft Fp ergibt sich also aus der Differenz der Kraft F0, die am unteren Ende der Wassersäule das Wasser durch den dort herrschenden (Umgebungs-)Druck p0 nach oben drückt, und der Kraft F1 am oberen Ende der Wassersäule, mit der der innere Trinkhalmdruck p1 das Wasser nach unten drückt. In beiden Fällen wirken die Drücke auf denselben inneren Halmquerschnitt A, sodass die entsprechenden Kräfte anhand der Drücke ermittelt werden können (F=p⋅A).
\begin{align}
&F_p = F_0 – F_1 \\[5px]
&F_p = p_0 \cdot A – p_1 \cdot A \\[5px]
\label{ff}
&\underline{F_p = \left(p_0 – p_1 \right) \cdot A} \\[5px]
\end{align}
Diese nach oben wirkende Kraft Fp muss offensichtlich so groß sein, dass sie in der Lage ist die Wassersäule mit der Gewichtskraft Fg=m⋅g nach oben zu drücken. Die Gewichtskraft der im Halm hochzudrückenden Wassersäule hängt dabei vom Wasserstand im Halm ab. Mit zunehmender Steighöhe nimmt auch die Gewichtskraft der Wassersäule zu. Diese Gewichtskraft lässt sich über die Querschnittsfläche A der Flüssigkeitssäule (= Querschnittsfläche des Halms) und der Flüssigkeitsdichte ϱ wie folgt bestimmen:
\begin{align}
&F_g = m \cdot g ~~~~~\text{mit} ~~~ m = \rho V = \rho A h \\[5px]
&\underline{F_g = \rho gh \cdot A} \\[5px]
\end{align}
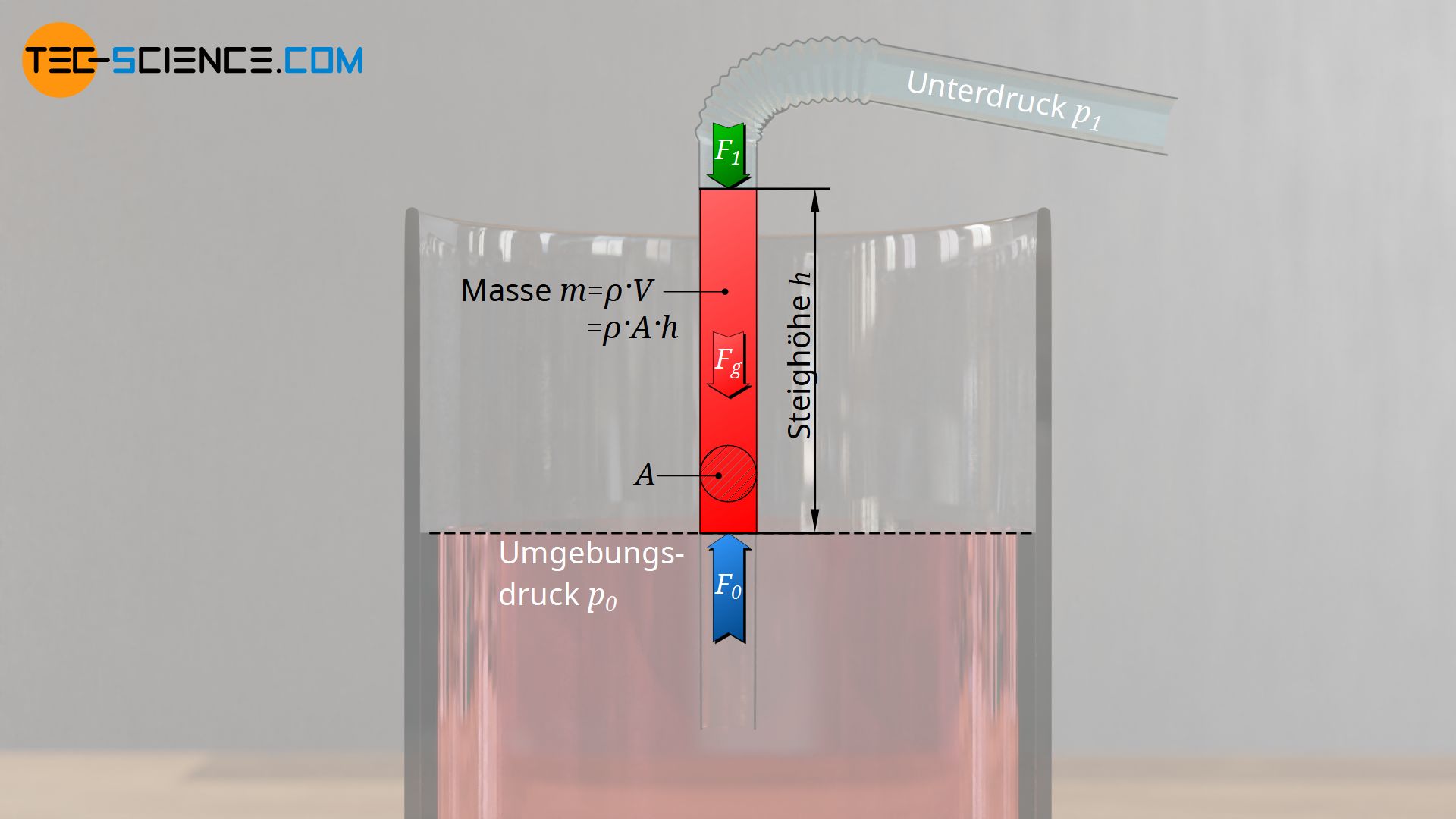
Mit zunehmendem Wasserstand im Halm wird die Gewichtskraft der Wassersäule also immer größer. Irgendwann wird die Gewichtskraft Fg schließlich so groß werden wie die nach oben wirkende Kraft Fp. In diesem Zustand ist es nun nicht mehr möglich das Wasser weiter nach oben zu drücken. Bei gegebenen Drücken ermittelt sich diese Steighöhe h wie folgt:
\begin{align}
\require{cancel}
F_p &\overset{!}{=} F_g \\[5px]
\left(p_0 – p_1 \right) \cdot \bcancel{A} & = \rho gh \cdot \bcancel{A} \\[5px]
p_0 – p_1 &= \rho h g \\[5px]
\end{align}
\begin{align}
&\underline{h = \frac{p_0 – p_1}{\rho g} } \\[5px]
\end{align}
Für die maximale mögliche Kraft mit der das Wasser nach oben gedrückt werden kann muss im Halminneren ein Vakuum (p1=0) herrschen, sodass der gesamte Umgebungsdruck p0 das Wasser ohne Gegendruck im Halminneren nach oben drücken kann. In diesem Fall erhält man die maximal mögliche Steighöhe hmax unter Erzeugung eines Vakuums im Halminneren:
\begin{align}
&h_{max} = \frac{p_0 – \overbrace{p_1}^{=0}}{\rho \cdot g} \\[5px]
&\boxed{h_{max} = \frac{p_0}{\rho \cdot g} }\\[5px]
\end{align}
Bei einem Umgebungsdruck von 1 bar und einer Flüssigkeitsdichte von 1000 kg/m³ sowie einer Fallbeschleunigung von 10 N/kg, beträgt die maximale Förderhöhe von Wasser somit rund 10 Meter:
\begin{align}
&\underline{h_{max}} = \frac{p_0}{\rho \cdot g} \approx \frac{10^5 \frac{\text{N}}{\text{m²}}}{1000 \frac{\text{kg}}{\text{m³}} \cdot 10 \frac{\text{N}}{\text{kg}}} = \underline{10 \text{ m}} \\[5px]
\end{align}
Es lässt sich folglich maximal aus einem 10 Meter hohen Trinkhalm trinken. Bei einem längeren Trinkhalm kann der Umgebungsdruck die Wassersäule nicht mehr höher fördern und würde in dieser Höhe einfach stehen bleiben.
Beachte, dass die Erzeugung eines Vakuums letztlich nur von theoretischer Natur ist. Denn mit sinkendem Druck, nimmt auch die Siedetemperatur von Flüssigkeiten ab. Wird der Druck also irgendwann zu gering, dann beginnt die Flüssigkeit im Halm zu verdampfen und die gasförmigen Teilchen bauen auf diese Weise wieder einen Druck auf, den sogenannten Dampfdruck. Bei einer Temperatur von 20 °C wird Wasser bspw. bei einem Druck von 23 mbar verdampfen. Der geringste Druck den man im statischen Gleichgewicht mit Wasser bei 20 °C erzielen kann, beträgt also 23 mbar und nicht etwa Vakuum. Man wird somit in der Praxis geringere maximale Saughöhen erzielen, als mit einem Vakuum theoretisch möglich.
Einfluss der Eintauchtiefe
Es wurde bereits angedeutet, dass die Eintauchtiefe keinen Einfluss auf die maximale Saughöhe hat. Dies soll im Folgenden mathematisch gezeigt werden. Hierzu wird die gesamte im Halm befindliche Wassersäule betrachtet, die nach oben bewegt wird. Die Kraft mit der diese Wassersäule effektiv nach oben gedrückt wird, ergibt sich wiederum aus der Differenz der Kräfte am unteren und oberen Ende der Wassersäule:
\begin{align}
&F_p = F_2 – F_1 \\[5px]
&F_p = p_2 \cdot A – p_1 \cdot A \\[5px]
\label{f}
&F_p = \left(p_2 – p_1 \right) \cdot A \\[5px]
\end{align}
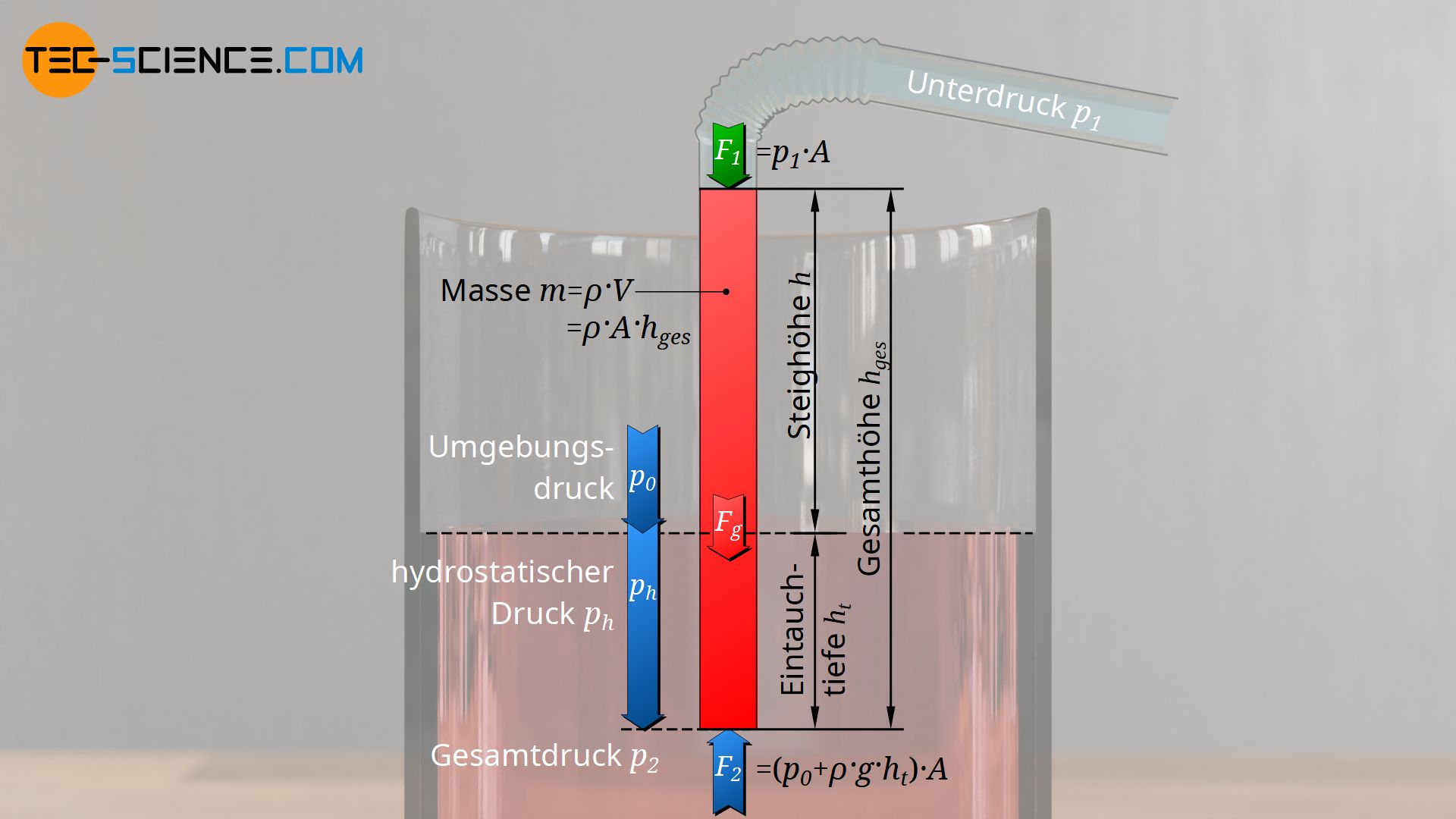
Der am unteren Ende des Trinkhalms wirkende Druck p2 ergibt sich aus der Summe von Umgebungsdruck p0 und hydrostatischem Druck ph (siehe hierzu Artikel Druck in Flüssigkeiten). Der hydrostatische Druck bestimmt sich dabei über die Dichte der Flüssigkeit ϱ, der Fallbeschleunigung g und der Tiefe unterhalb der Wasseroberfläche ht. Diese Tiefe ht entspricht dabei gerade der Eintauchtiefe des Trinkhalms.
\begin{align}
&p_2 = p_0 + p_h \\[5px]
\label{p}
&p_2 = p_0 + \rho g h_t \\[5px]
\end{align}
Wird Gleichung (\ref{p}) in Gleichung (\ref{f}) eingesetzt, dann gilt für die nach oben wirkende Kraft Fp:
\begin{align}
&F_p = \left(p_2 – p_1 \right) \cdot A \\[5px]
&\underline{F_p = \left(p_0 + \rho g h_t – p_1 \right) \cdot A} \\[5px]
\end{align}
Diese nach oben wirkende Kraft Fp muss nun wieder so groß sein, dass sie in der Lage ist die Wassersäule mit der Gewichtskraft Fg=m⋅g nach oben zu drücken. Die Gesamthöhe der Wassersäule im Halm hges ergibt sich aus der Summe von Eintauchtiefe unterhalb der Wasseroberfläche ht und Wasserstand oberhalb der Wasseroberfläche h. Die Gewichtskraft dieser Wassersäule lässt sich somit wie folgt über die Querschnittsfläche A und der Flüssigkeitsdichte ϱ bestimmen:
\begin{align}
&F_g = m \cdot g ~~~~~\text{mit} ~~~ m = \rho \cdot V = \rho \cdot A \cdot h_{ges} = \rho \cdot A \cdot (h_t+h) \\[5px]
&F_g = \rho g \left(h_t+h \right) \cdot A \\[5px]
&\underline{F_g = \left(\rho g h_t+ \rho g h\right) \cdot A} \\[5px]
\end{align}
Im statischen Gleichgewicht muss wieder die Gewichtskraft Fg genau so groß sein wie die nach oben wirkenden Kraft Fp. Die sich hieraus ergebende Steighöhe h bestimmt sich wie folgt:
\begin{align}
\require{cancel}
F_p &\overset{!}{=} F_g \\[5px]
\left(p_0 + \rho g h_t – p_1 \right) \cdot \bcancel{A} & = \left(\rho g h_t+ \rho g h\right) \cdot \bcancel{A} \\[5px]
p_0 + \bcancel{\rho g h_t} – p_1 &= \bcancel{\rho g h_t}+ \rho g h \\[5px]
p_0 – p_1 &= \rho h g \\[5px]
\end{align}
\begin{align}
&\underline{h = \frac{p_0 – p_1}{\rho g} } \\[5px]
\end{align}
Auch unter Berücksichtigung der Eintauchtiefe und des dort herrschenden hydrostatischen Drucks, zeigt sich also dieselbe Formel, sodass die maximale Förderhöhe tatsächlich nicht von der Eintauchtiefe ht abhängig ist!
Hierfür gibt es auch eine anschauliche Erklärung, denn aufgrund des hydrostatischen Drucks wird das Wasser im offenen Rohr ohnehin auf ein einheitliches Niveau gedrückt. Im Rohr wird sich gemäß dem Prinzip der kommunizierenden Röhren also immer automatisch derselbe Wasserpegel wie außerhalb einstellen. Insofern muss der Umgebungsdruck also gar nicht das Wasser im Rohr bis auf den umgebenden Wasserspiegel hochdrücken – dies übernimmt der hydrostatische Druck bereits von selbst. Der Umgebungsdruck ist somit nur verantwortlich für das Hochdrücken des Wasser ausgehend des umgebenden Wasserspiegels. Die maximale Förderhöhe bezieht sich also stets auf die Wasseroberfläche!






