Die barometrische Höhenformel beschreibt die Abnahme des Luftdrucks mit zunehmender Höhe.
Einleitung
Auf Meereshöhe beträgt der atmosphärische Luftdruck rund 1 bar. Die Praxis zeigt aber, dass der Luftdruck mit steigender Höher mehr und mehr abnimmt. Auf einem 2000 Meter hohen Berg beträgt der Atmosphärendruck bspw. nur noch ca. 0,8 bar. Auf dem Mount Everest in einer Höhe von 8848 Metern übt die Luft sogar nur noch einen Druck von 0,3 bar aus.
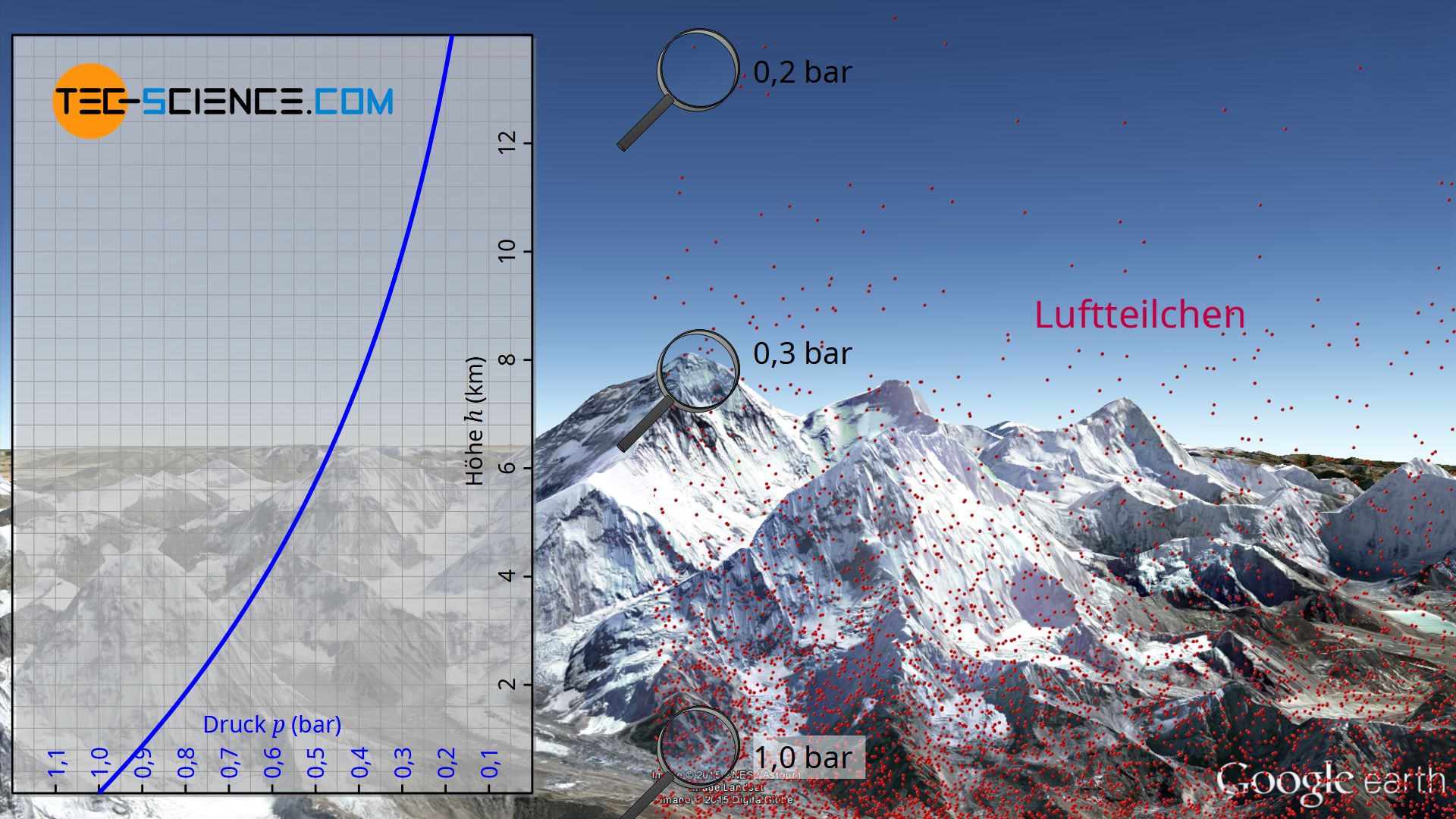
Mit Hilfe des Teilchenmodells lässt sich dieses Phänomen anschaulich nachvollziehen. Alle Gasteilchen besitzen letztlich eine Masse, und sei sie noch so klein. Dies führt letztlich dazu, dass auch Gasteilchen der Erdanziehung unterliegen. Zwischen den Teilchen finden zwar permanent Kollisionen statt und die Moleküle fliegen anschließend scheinbar in zufällige Richtungen wieder davon. Gerade bei sehr großen Abmessungen zeigt sich aber, dass sich die Luftteilchen aufgrund der wirkenden Erdanziehungskraft eher nahe der Erdoberfläche befinden. Aufgrund dieser Erdanziehung werden die Luftteilchen sozusagen nach unten gezogen, wo sie anschließend wieder mit anderen Luftteilchen zusammenprallen und in die Luft geschleudert werden.
Dieses Verhalten kann man in einem Modell anschaulich nachbilden. Hierzu wird werden kleine Kugeln in eine senkrecht stehende Glasröhre eingefüllt. Das quaderförmige Glasrohr steht dabei auf einer oszillierenden Platte. Die Vibration verleiht den Kugeln eine zufällige Geschwindigkeit. Hierdurch prallen die Kugeln schließlich auch untereinander permanent zusammen, so wie dies die Moleküle in der Luft tun. Die Kugeln katapultieren sich wie die realen Luftteilchen in zufällige Höhen.
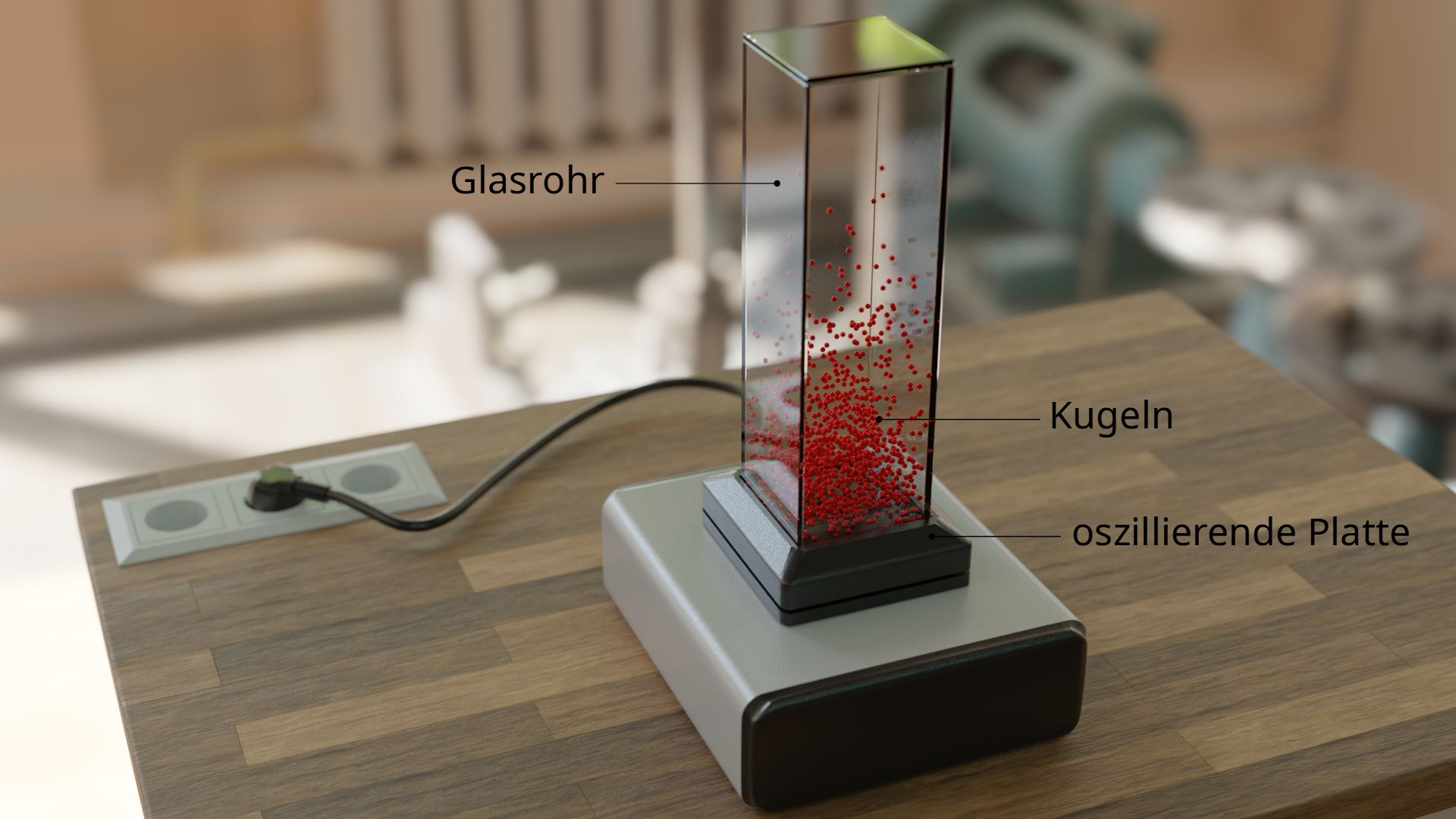
Es kann schließlich beobachtet werden, dass sich der Großteil der Kugeln nahe der Rüttelplatte befindet. Mit zunehmender Höhe nimmt die Kugeldichte ab, da nur wenige Kugeln in solch einer Weise kollidieren, dass sie sich mehrfach in die Höhe katapultieren. Eine solche Dichteverteilung über die Höhe hinweg, findet man letztlich auch bei den Molekülen der Luft wieder! Die Dichte der Luft nimmt ebenfalls mit zunehmender Höhe immer mehr ab, da immer weniger Luftmoleküle in solch große Höhen vordringen können. Dies ist auch der Grund weshalb viele Bergsteiger bei großen Höhen zusätzlichen Sauerstoff in Pressluftflaschen mitführen. Denn die geringe Anzahl an Luftteilchen reicht oft nicht mehr aus, um den Körper mit ausreichend Sauerstoff zu versorgen.
In der verringerten Luftdichte, ist auch direkt der abnehmende Luftdruck begründet. Im Artikel Druck in Gasen wurde bereits ausführlich erläutert, dass der Druck in Gasen durch Stoßprozesse der Teilchen mit Grenzflächen zustande kommt. Eine verringere Teilchendichte bedeutet somit auch eine geringe Anzahl an Kollisionen. Dies wiederum hat einen geringeren ausgeübten Druck des Gases zur Folge.
Der abnehmende Luftdruck mit zunehmender Höhe ist der verringerten Luftdichte geschuldet. Die Verringerung der Luftdichte ist wiederum dadurch begründet ist, dass auch Luftteilchen der Erdanziehung unterliegen und sich somit vermehrt nahe der Erdoberfläche aufhalten!
Herleitung der barometrischen Höhenformel
Die Abnahme des Drucks mit zunehmender Höher kann durch eine Kräftebilanz mathematisch hergeleitet werden. Hierfür wird in einer beliebigen Höhe h eine dünne Luftschicht mit der Grundfläche A und der Höhe Δh betrachtet. Die Luft innerhalb dieser Schicht hat dabei eine bestimmte Masse Δm. Man kann sich die Luftschicht als von einer unsichtbaren Hülle umgeben vorstellen, d.h. als eine Art Luftpaket. Betrachtet man diese Luftschicht als ruhend, dann steht sie steht im Gleichgewicht mit der umgebenden Luft. Ein solches Kräftegleichgewicht würde prinzipiell auch dann gelten, wenn sich die Luftschicht mit konstanter Geschwindigkeit nach oben oder unten bewegt, auch wenn dann Reibungskräfte berücksichtigt werden müssten.
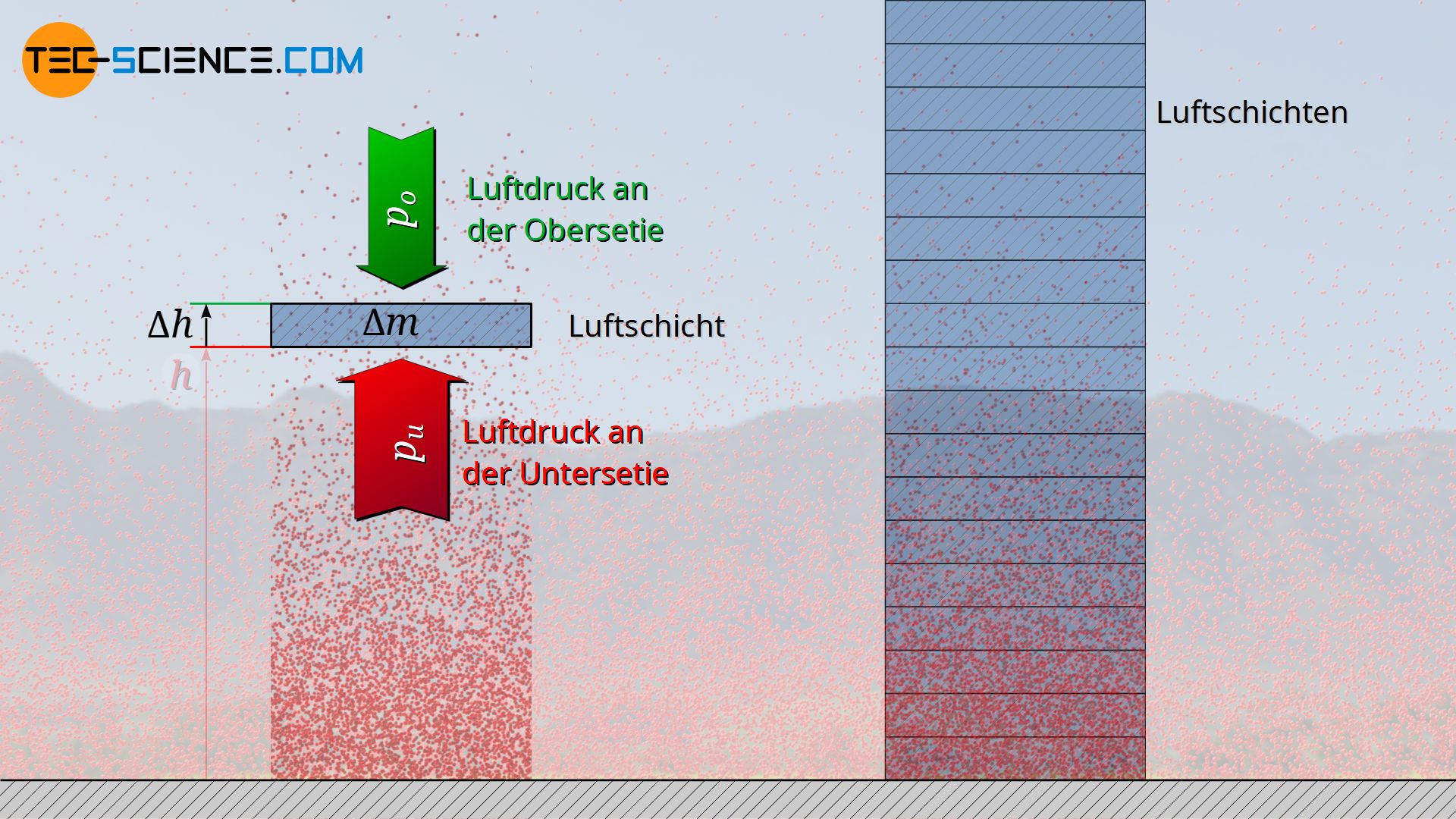
Aufgrund dieses Gleichgewichtes lässt sich nun anschaulich nachvollziehen, weshalb der Luftdruck unterhalb der Luftschicht unweigerlich größer sein muss als oberhalb. Die umgebenden Luftteilchen üben durch Stoßprozesse mit dem gedachten Luftsack sowohl von unten als auch von oben einen entsprechenden Druck hierauf aus. Nur wenn der nach oben gerichtete Druck an der Unterseite aber größer ist als der nach unten wirkenden Druck an der Oberseite, kann effektiv eine Kraft nach oben wirken. Diese nach oben wirkenden Kraft wirkt der Gewichtskraft der Luftschicht entgegen und hält sie somit stabil in der Luft hält.
Der Druck an der Unterseite einer betrachteten Luftschicht muss größer sein als an der Oberseite, damit die Gewichtskraft der Luftschicht durch die nach oben gerichtete Kraft ausgeglichen werden kann!
Die Atmosphäre kann man sich nun aus unzählig vielen dünnen Luftschichten aufgebaut vorstellen. Von Luftschicht zu Luftschicht muss also der Luftdruck permanent abnehmen, damit die einzelnen Schichten durch die größere Kraft an der Unterseite jeweils im Gleichgewicht gehalten werden können. Für eine genauere mathematische Beschreibung, müssen die wirkenden Kräfte an den Luftschichten nun genauer betrachtet werden.
Zusammenhang zwischen Höhenänderung und Druckänderung bei gegebener Dichte
Hierzu wird zunächst der Druck an der Unterseite einer Luftschicht näher betrachtet. Die nach oben gerichtete Kraft Fu die durch den dort wirkenden Luftdruck p entsteht, ergibt sich aus dem Produkt von Druck und Fläche A des Volumenelementes:
\begin{align}
&F_u = p \cdot A ~~~~~\text{Kraft an der Unterseite der Luftschicht} \\[5px]
\end{align}
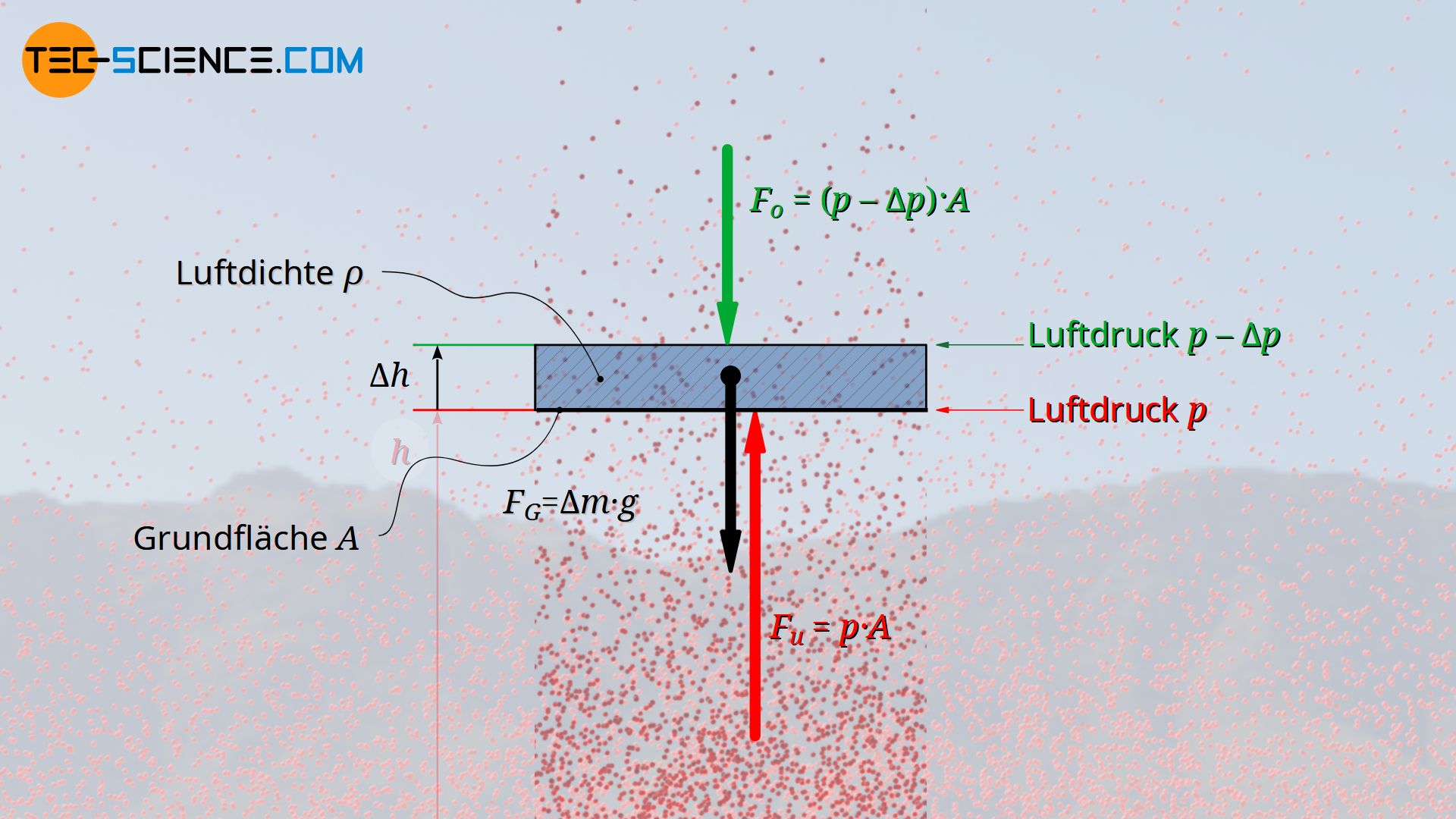
An der Oberseite der Luftschicht, wird sich der Luftdruck um einen bestimmten Betrag Δp verringert haben. Für die nach unten gerichtete Kraft, die dieser Druck auf auf die Oberseite der Luftschicht ausübt, gilt folglich:
\begin{align}
&F_o = \left(p-\Delta p \right) \cdot A ~~~~~\text{Kraft an der Oberseite der Luftschicht} \\[5px]
\end{align}
Die Masse Δm der betrachteten Luftschicht kann aus dessen Volumen ΔV und der darin vorhandenen Luftdichte ϱ ermittelt werden (Δm=ΔV⋅ϱ). Wie bereits erläutert, wird die Luftdichte zwar mit zunehmender Höher abnehmen, da aber in diesem Fall nur eine sehr dünne Luftschicht betrachtet wird, kann innerhalb dieser Luftschicht von einer konstanten Dichte ausgegangen werden. Mit A als Grundfläche und Δh als Höhe der Luftschicht, ergibt sich die angreifende Gewichtskraft wie folgt:
\begin{align}
&F_G = \Delta m \cdot g \\[5px]
&F_G= \Delta V \cdot \rho \cdot g \\[5px]
&F_G= A \cdot \Delta h \cdot \rho \cdot g ~~~~~\text{Gewichtskraft der Luftschicht} \\[5px]
\end{align}
Die nach unten gerichtete Gewichtskraft FG und die ebenfalls nach unten gerichtete Kraft auf die Oberseite der Luftschicht Fo, muss nun im Gleichgewicht mit der nach oben wirkenden Kraft an der Unterseite Fu stehen. Auf diese Weise kann schließlich folgender Zusammenhang zwischen einer Höhenänderung Δh (Dicke der Luftschicht) und dem damit verbunden Betrag der Druckänderung Δp hergeleitet werden.
\begin{align}
\require{cancel}
& F_u \overset{!}{=} F_G + F_o \\[5px]
& p \cdot \bcancel{A} = \bcancel{A} \cdot \Delta h \cdot \rho \cdot g + \left(p-\Delta p \right) \cdot \bcancel{A} \\[5px]
&\bcancel{p} = \Delta h \cdot \rho \cdot g + \bcancel{p} – \Delta p \\[5px]
\label{dp}
&\underline{\Delta p = \rho \cdot g \cdot \Delta h} ~~~~~\text{gilt nur für geringe Höhenänderungen }\Delta h \\[5px]
\end{align}
Beachte, dass diese Formel nur gilt, wenn die Höhenänderung Δh nicht zu groß gewählt wird, da nur in einem solchen Fall von einer näherungsweise konstanten Luftdichte ϱ ausgegangen werden kann. Bei zu großen Höhenänderungen ist die Dichte innerhalb der Luftschicht nicht mehr konstant. In diesem Fall müsste man mit einer mittleren Luftdichte rechnen.
Zusammenhang zwischen Höhenänderung und Druckänderung bei gegebener Temperatur
In der Praxis kann man davon ausgehen, dass sich innerhalb eines Höhenunterschiedes von 100 Metern, die Luftdichte nicht merklich ändern wird und deshalb als konstant angesehen werden kann. Nimmt man an, dass die Luftdichte in Bodennähe etwa 1,2 kg/m³ beträgt, dann wird sich gemäß der oberen Formel in 100 Metern Höhe eine Druckänderung von etwa 12 mbar ergeben:
\begin{align}
&\Delta p = \rho \cdot g \cdot \Delta h = 1,2 \tfrac{\text{kg}}{\text{m³}}\cdot 10 \tfrac{\text{N}}{\text{kg}} \cdot 100 \text{ m} = 120 \text{ Pa} = 12 \text{ mbar} \\[5px]
\end{align}
Hatte der Druck am Boden bspw. 1,0 bar betragen, so wird er in 100 Metern Höhe folglich um 12 mbar auf insgesamt 0,988 bar gesunken sein. Man könnte nun für die nächsten 100 Metern dieselbe Rechnung aufstellen, um hierdurch den Druck in 200 Metern Höhe zu berechnen. Man muss aber beachten, dass sich mit jedem Höhenunterschied letztlich auch die Luftdichte leicht ändert. Die Luft wird mit zunehmender Höhe dünner, d.h. die Luftdichte nimmt ab. Man muss deshalb für jeden sich neu ergebenden Druck auch die sich neu ergebende Luftdichte zugrunde legen.
Dies kann zum Beispiel mithilfe der thermischen Zustandsgleichung idealer Gase geschehen, gemäß deren Dichte und Druck direkt über die Temperatur miteinander verknüpft sind:
\begin{align}
\label{ideal}
&\boxed{p=R_s \cdot \rho \cdot T}~~~~~\text{ideale Gasgleichung} \\[5px]
\label{rho}
&\rho=\frac{p}{ R_s \cdot T }\\[5px]
\end{align}
In dieser Gleichung bezeichnet T die absolute Temperatur in Kelvin und Rs die spezifische Gaskonstante. In diesem Fall wird von trockener Luft mit einer spezifischen Gaskonstante von Rs=287 J(kg⋅K) ausgegangen. Wird an dieser Stelle Gleichung (\ref{rho}) in Gleichung (\ref{dp}) eingesetzt, dann kann die Druckänderung bei bekannter Temperatur wie folgt ermittelt werden:
\begin{align}
&\Delta p = \rho \cdot g \cdot \Delta h \\[5px]
&\Delta p = \frac{p}{ R_s \cdot T } \cdot g \cdot \Delta h \\[5px]
\label{dr}
&\underline{\Delta p = \frac{g}{ R_s \cdot T } \cdot p \cdot \Delta h} \\[5px]
\end{align}
Welchen Vorteil bietet nun diese Gleichung im Vergleich zur Gleichung (\ref{dp}), denn schließlich zeigt die Praxis, dass eben nicht nur die Dichte, sondern auch die Temperatur mit zunehmender Höhe geringer wird (beides zunächst also unbekannte Verläufe)? Dies ist prinzipiell richtig, jedoch ändert sich die Temperatur mit zunehmender Höhe weniger stark im Vergleich zur Dichte. Für geringe Höhenunterschiede ist die Annahme einer konstanten Temperatur deshalb meist gerechtfertigter als die Annahme einer konstanten Dichte!
Unterhalb von 10 km Höhe nimmt zum Beispiel die Luftdichte im Mittel um etwa 1,5 % innerhalb von 100 Metern Höhe ab (Temperaturänderungen eingerechnet). Im Vergleich hierzu fällt die Temperatur (in Kelvin!) hingegen im Mittel nur um etwa 0,4 %. Der Einfluss der Temperaturänderung ist also nicht einmal ein Drittel so groß im Vergleich zum Einfluss der Dichteänderung. Im Artikel Erweiterte barometrische Höhenformel wird der Einfluss der Temperaturabnahme auf den Druckverlauf näher diskutiert.
Der Einfachheit halber soll im Folgenden aber stets von einer konstanten Temperatur ausgegangen werden. Man spricht in diesem Zusammenhang auch von einer isothermen Atmosphäre. Ebenso soll die Abnahme der Fallbeschleunigung mit zunehmender Höhe unberücksichtigt bleiben und die spezifische Gaskonstante trotzt sich evtl. ändernder atmosphärischer Zusammensetzung als konstant betrachtet werden.
Tatsächlich spielt die Abnahme der Fallbeschleunigung in der Praxis meist keine Rolle. So nimmt bis auf 100 km Höhe die Fallbeschleunigung nur um 3 % ab. Für das Wetter sind gar ohnehin nur die unteren 15 km relevant, die sogenannte Troposphäre (Wetterschicht). Auch der Einfluss der chemischen Zusammensetzung spielt unterhalb von 100 km Höhe keine Rolle, da die Atmosphärengase bis dahin gut durchmischt sind. Man spricht unterhalb von 100 km Höhe deshalb auch von der Homosphäre. Die unter Abbildung und Animation zeigt die Einteilung der Erdatmosphäre in verschiedene Schichten. Diese Einteilung erfolgt aufgrund der verschiedenen Temperaturen bzw. der charakteristischen Temperaturverläufe innerhalb dieser Schichten (im Artikel Erweiterte barometrische Höhenformel mehr hierzu).

Bei Anwendung der Formel (\ref{dr}) muss man stets beachten, dass eine positive Änderung der Höhe (Δh>0) im mathematischen Sinne jedoch eine negative Änderung des Drucks zur Folge hat (Δp<0), da der Druck mit zunehmender Höhe ja schließlich abnimmt. Für eine korrekte mathematische Beschreibung muss die obere Gleichung deshalb noch mit einem negativen Vorzeichen versehen werden. Dies wird für die im nachfolgend hergeleitete barometrische Höhenformel noch wichtig.
\begin{align}
\label{a}
&\boxed{\Delta p = -\frac{g}{R_s \cdot T} \cdot p \cdot \Delta h} ~~~~~\text{gilt nur für geringe Höhenänderungen }\Delta h \\[5px]
\end{align}
Zusammenhang zwischen Druck und Höhenänderung
Wie anhand der beschriebenen Vorgehensweise im vorherigen Abschnitt erläutert, bietet es sich für die Berechnung der Druckänderung für große Höhen an, diese zunächst in kleine Luftschichten von bspw. 100 Metern zu unterteilen. Anschließend sind alle Druckänderungen zur gesamten Druckänderung aufzusummieren. Diese Vorgehensweise ist jedoch recht aufwendig. Die Differential- bzw. Integralrechnung der Mathematik bietet an dieser Stelle eine einfachere und allgemeinere Methode.
Hierzu werden die makroskopischen Höhenunterschiede immer kleiner und kleiner gewählt. Im Grenzfall erhält man infinitesimale, d.h. unendlich kleine Höhenunterschiede bzw. Druckunterschiede. In Abgrenzung zu den makroskopischen Differenzen Δh bzw. Δp erhält man schließlich die entsprechenden Differentiale dh bzw. dp. Spätestens an dieser Stelle löst sich auch automatisch das Problem mit der konstanten Dichte bzw. konstanten Temperatur innerhalb der einzelnen Luftschichten, da im Folgenden ohnehin unendlich kleine Höhenunterschiede betrachtet werden.
Für den Zusammenhang zwischen einer infinitesimalen Höhendifferenz dh und der hieraus resultierenden, infinitesimalen Druckänderung dp gilt somit analog zu Gleichung (\ref{a}):
\begin{align}
\label{c}
&\boxed{\text{d}p = -\frac{g}{R_s \cdot T} \cdot p \cdot \text{d} h} \\[5px]
\end{align}
Die zum Druckdifferential dp gehörende Druckvariable p wird nun auf die linke Seite des Gleichheitszeichens gebracht, sodass beide zusammenhängende Größen völlig getrennt vom Höhendifferential dh auf der rechten Seite der Gleichung stehen (Trennung der Variablen genannt):
\begin{align}
&\frac{1}{p} ~ \text{d}p = -\frac{g}{R_s \cdot T} \cdot p \cdot \text{d} h \\[5px]
\end{align}
Beide Seiten der Gleichung sind nun innerhalb der entsprechenden Grenzen zu integrieren. Ausgehend eines bekannten Ausgangsdruckes p0 auf der Höhe h0 kann man hieraus den Druck p in einer beliebigen Höhe h wie ermitteln. Beachte, dass Temperatur, Fallbeschleunigung und spezifische Gaskonstante als konstant angenommen werden und somit als Konstanten zu betrachten sind. Die Konstanten können deshalb vor das Integral geschrieben werden.
\begin{align}
&\int_{p_0}^{p}\frac{1}{p} ~ \text{d}p = \int_{h_0}^h-\frac{g}{R_s \cdot T} \cdot \text{d} h \\[5px]
&\int_{p_0}^{p}\frac{1}{p} ~ \text{d}p =-\frac{g}{R_s \cdot T} \cdot \int_{h_0}^h \text{d} h \\[5px]
&\left[\ln{\left( p\right)}\right]_{p_0}^p = -\frac{g}{R_s \cdot T} \cdot \left[~h~\right]_{h_0}^{h}\\[5px]
& \ln{(p)}-\ln{(p_0)}= -\frac{g}{R_s \cdot T} \cdot \underbrace{\left(h-h_0\right)}_{\Delta h}\\[5px]
\end{align}
Die Differenz zwischen der Höhe h (für den der Druck p ermittelt werden soll) und der Ausgangshöhe h0 (in der der Ausgangsdruck p0 herrscht), entspricht gerade der betrachteten Höhenänderung Δh.
\begin{align}
& \ln{(p)}-\ln{(p_0)}= -\frac{g \cdot \Delta h}{R_s \cdot T} \\[5px]
\end{align}
Auch die linke Seite der Gleichung lässt sich etwas umformulieren. Gemäß den Logarithmengesetzen kann nämlich die Differenz zweier logarithmierter Zahlen auch als logarithmierter Quotient dieser Zahlen ausgedrückt werden [ln(a)-ln(b)=ln(a/b)]. Man erhält also:
\begin{align}
& \ln{\left(\frac{p}{p_0}\right)}= -\frac{g \cdot \Delta h}{R_s \cdot T} \\[5px]
\end{align}
Um diese Gleichung nun nach dem gesuchten Druck p aufzulösen, bedient man sich eines Tricks. Hierzu werden beide Seiten der Gleichung in den Exponenten der natürlichen Exponentialfunktion („e-Funktion“) geschrieben:
\begin{align}
& \text{e}^{\Large{\ln{\left(\frac{p}{p_0}\right)}}}= \text{e}^{\Large{-\frac{g \cdot \Delta h}{R_s \cdot T} }}\\[5px]
\end{align}
Da der natürliche Logarithmus („ln“) gerade die Umkehrfunktion der e-Funktion ist gilt ganz allgemein: eln(a)=a. Das Ergebnis der linken Seite entspricht somit gerade dem Quotienten p/p0. Auf diese Weise lässt sich der Druck p in einer bestimmten Höhe Δh über einem Referenzniveau mit dem Ausgangsdruck p0 wie folgt berechnen:
\begin{align}
&\frac{p}{p_0}= \text{e}^{-\frac{g \cdot \Delta h}{R_s \cdot T} }\\[5px]
\label{bar}
&\boxed{p(\Delta h)= p_0 \cdot \text{e}^{\Large{-\frac{g \cdot \Delta h}{R_s \cdot T}}}} ~~~~~\text{barometrische Höhenformel} \\[5px]
\end{align}
Diese Formel wird schließlich barometrsiche Höhenformel genannt und gibt den Druck p in Abhängigkeit der Höhe Δh über einem Bezugsniveau mit bekanntem Ausgangsdruck p0 an. Im Vergleich zur Formel (\ref{a}) liefert die barometrische Höhenformel auch über größere Höhenbereiche hinweg eine höhere Genauigkeit. Aber auch dabei muss beachtet werden, dass diese Formel unter der Voraussetzung hergeleitet wurde, dass sich weder Temperatur und Fallbeschleunigung mit der Höhe ändern, noch die spezifische Gaskonstante (d.h. die Zusammensetzung der Atmosphäre). Strenggenommen gilt diese Formel also auch wiederum nur für geringe Höhenunterschiede, bei deren diese Bedingungen in guter Näherung erfüllt sind.
Mit einem Standarddruck von p0=1,013 bar auf Meereshöhe (h0=0) und einer Temperatur von T0= 288 K (15 °C) sowie einer spezifischen Gaskonstante von Rs=287 J(kg⋅K), beträgt die Abweichung der barometrischen Höhenformel verglichen mit der Standardatmosphäre aus der Luftfahrt unterhalb einer Höhe von 3 km maximal 1 %. In 6 Kilometern Höhe nimmt die Abweichung auf ca. 5 % zu und steigt immer mehr an. In 12 Kilometern Höhe erreicht die Abweichung etwa 27 %. Die Abweichungen sind hauptsächlich auf die nicht berücksichtigte Temperaturänderung zurückzuführen.
Die barometrische Höhenformel kann nicht nur über die Temperatur ausgedrückt werden, sondern auch über die Dichte auf Bezugsniveau. Hierzu wird das Produkt aus spezifischer Gaskonstante und Temperatur in der barometrischen Höhenformel (\ref{bar}) gemäß der thermischen Zustandsgleichung (\ref{bar}) durch den Quotienten aus Druck und Dichte ersetzt:
\begin{align}
&p=R_s \cdot \rho \cdot T \\[5px]
&p_0=R_s \cdot \rho_0 \cdot T \\[5px]
&\underline{R_s \cdot T = \frac{p_0}{\rho_0}} \\[5px]
\end{align}
Wird dieser Ausdruck nun in Gleichung (\ref{bar}) eingesetzt, dann folgt:
\begin{align}
&p= p_0 \cdot \text{e}^{-\frac{g \cdot \Delta h}{R_s \cdot T}} ~~~~~\text{mit}~R_s \cdot T = \frac{p_0}{\rho_0} ~\text{folgt:} \\[5px]
\label{bar2}
&\boxed{p(\Delta h)= p_0 \cdot \text{e}^{\Large{-\frac{g \cdot \rho_0 \cdot \Delta h}{p_0}}}} ~~~~~\text{barometrische Höhenformel} \\[5px]
\end{align}
Zusammenhang zwischen Höhenänderung und Dichte
Da die Dichte gemäß Gleichung (\ref{rho}) in direktem Zusammenhang mit dem Druck steht, kann über die barometrische Höhenformel auch die Abnahme der Dichte mit zunehmender Höhe bestimmt werden. Hierzu ist die barometrische Höhenformel (\ref{bar}) lediglich in Gleichung (\ref{rho}) einzusetzen:
\begin{align}
\label{x}
&\rho=\frac{p}{ R_s \cdot T}\\[5px]
\label{y}
&\rho(\Delta h)=\frac{p(\Delta h)}{ R_s \cdot T}= \frac{ p_0 \cdot \text{e}^{\Large{-\frac{g \cdot \Delta h}{R_s \cdot T}}} }{ R_s \cdot T}= \underbrace{\frac{p_0}{ R_s \cdot T}}_{\rho_0} \cdot \text{e}^{\Large{-\frac{g \cdot \Delta h}{R_s \cdot T}}} \\[5px]
\label{z}
&\boxed{\rho(\Delta h)= \rho_0 \cdot \text{e}^{\Large{-\frac{g \cdot \Delta h}{R_s \cdot T}}}} \\[5px]
\end{align}
In Gleichung (\ref{y}) wurde ausgenutzt, dass der Term p0/(Rs⋅T) gemäß Gleichung (\ref{x}) der Ausgangsdichte ϱ0 auf Bezugsniveau entspricht. Ebenso kann der Term Rs⋅T in Gleichung (\ref{z}) durch p0/ϱ0 ersetzt werden. Man erhält dann die Abhängigkeit der Dichte ausgehend des Drucks p0 auf Bezugsniveau:
\begin{align}
&\boxed{\rho(\Delta h)= \rho_0 \cdot \text{e}^{\Large{-\frac{g \cdot \rho_0 \cdot \Delta h}{p_0}}}} \\[5px]
\end{align}
Vergleicht man den Verlauf der Dichte gemäß der barometrischen Höhenformel mit dem Dichteverlauf der Standardatmosphäre, so zeigen sich vor allem für Höhen unterhalb 3 km größere Abweichungen mit bis zu 7 %. Diese relativ großen Abweichungen sind auf die als konstant vorausgesetzte Temperatur zurückzuführen, die in der Realität jedoch abnimmt und auf diese Weise die Dichte stark beeinflusst. Mit zunehmender Höhe kompensiert der Fehler der bei der Berechnung des Drucks gemacht wird (und der für die Berechnung der Dichte ja zugrunde gelegt wird), die Abweichung aufgrund der nicht-konstanten Temperatur wieder. Die maximale Abweichung der Dichte von der Standardatmosphäre beträgt 10 % in einer Höhe 9 km und nimmt ab da sogar wieder ab.
Barometrische Höhenformel vs. hydrostatische Grundgleichung
Man kann die barometrische Höhenformel für kompressible Gase in Analogie zur hydrostatischen Grundgleichung für inkompressible Flüssigkeiten betrachten. Mit der zunehmenden Tiefe von der Flüssigkeitsoberfläche nimmt der Druck aufgrund den darüber befindlichen Flüssigkeitsschichten mehr und mehr zu. Auf prinzipiell dieselbe Weise steigt der Druck der Atmosphäre, wenn man sich ausgehend von großen Höhen in Richtung Erdoberfläche bewegt. Wir leben sozusagen auf dem Grund eines „Luftmeeres“. Unterschied zwischen dem Gas der Atmosphäre und der Flüssigkeit der Meere besteht lediglich darin, dass es sich Flüssigkeiten nicht komprimieren lassen. D.h. der Druck steigt in Flüssigkeiten (fast) ohne Zunahme der Dichte, während in Gasen die Dichte mit zunehmendem Druck ebenfalls zunimmt.
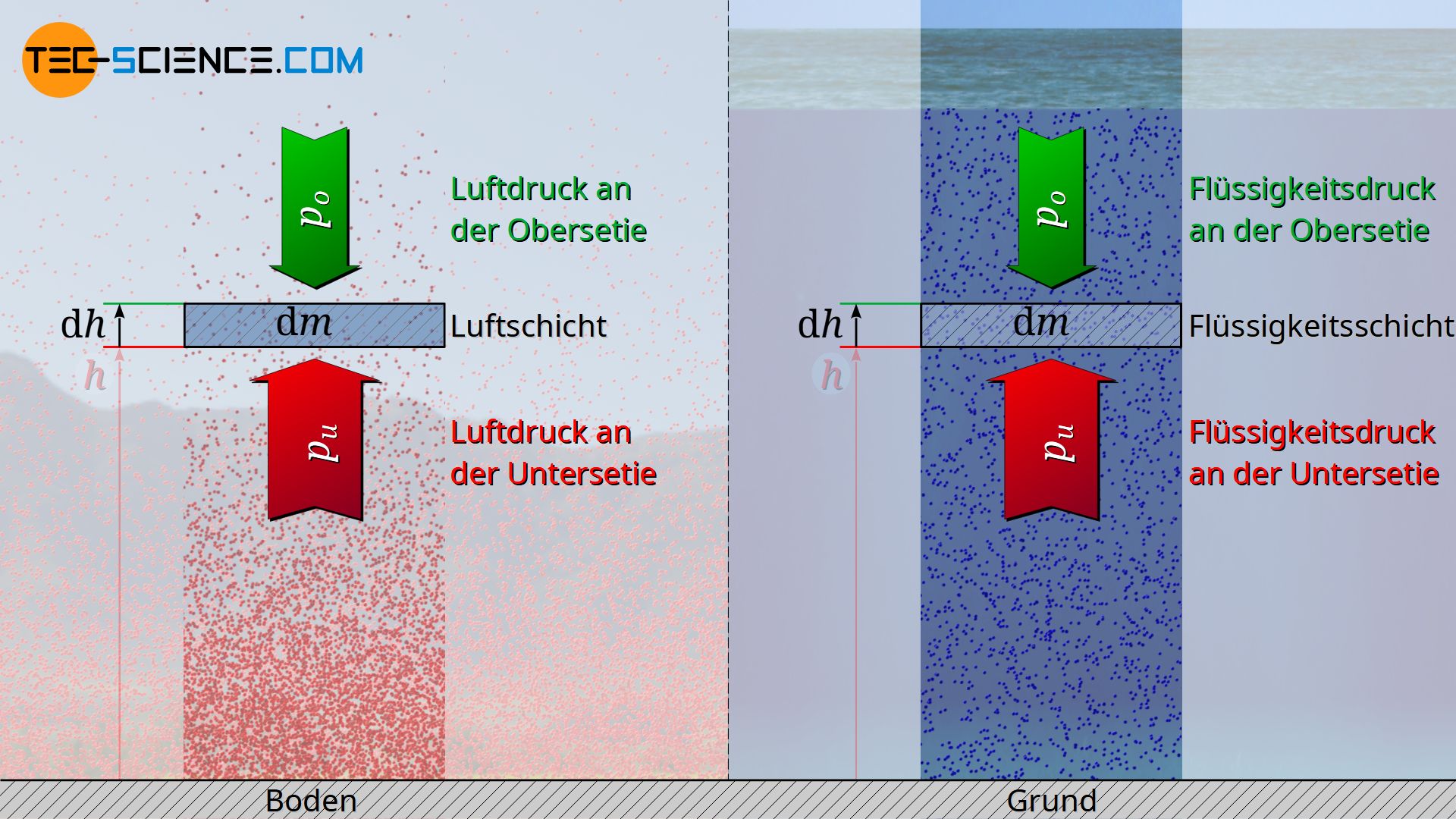
Man kann die hydrostatische Grundgleichung für inkompressible Flüssigkeiten auch aus den bisherigen Betrachtungen herleiten. Hierzu ist lediglich Gleichung (\ref{dp}) in infinitesimaler Schreibweise zu verwenden. Anschließend kann man diese Gleichung unter der Annahme einer konstanten Dichte ϱ integrieren.
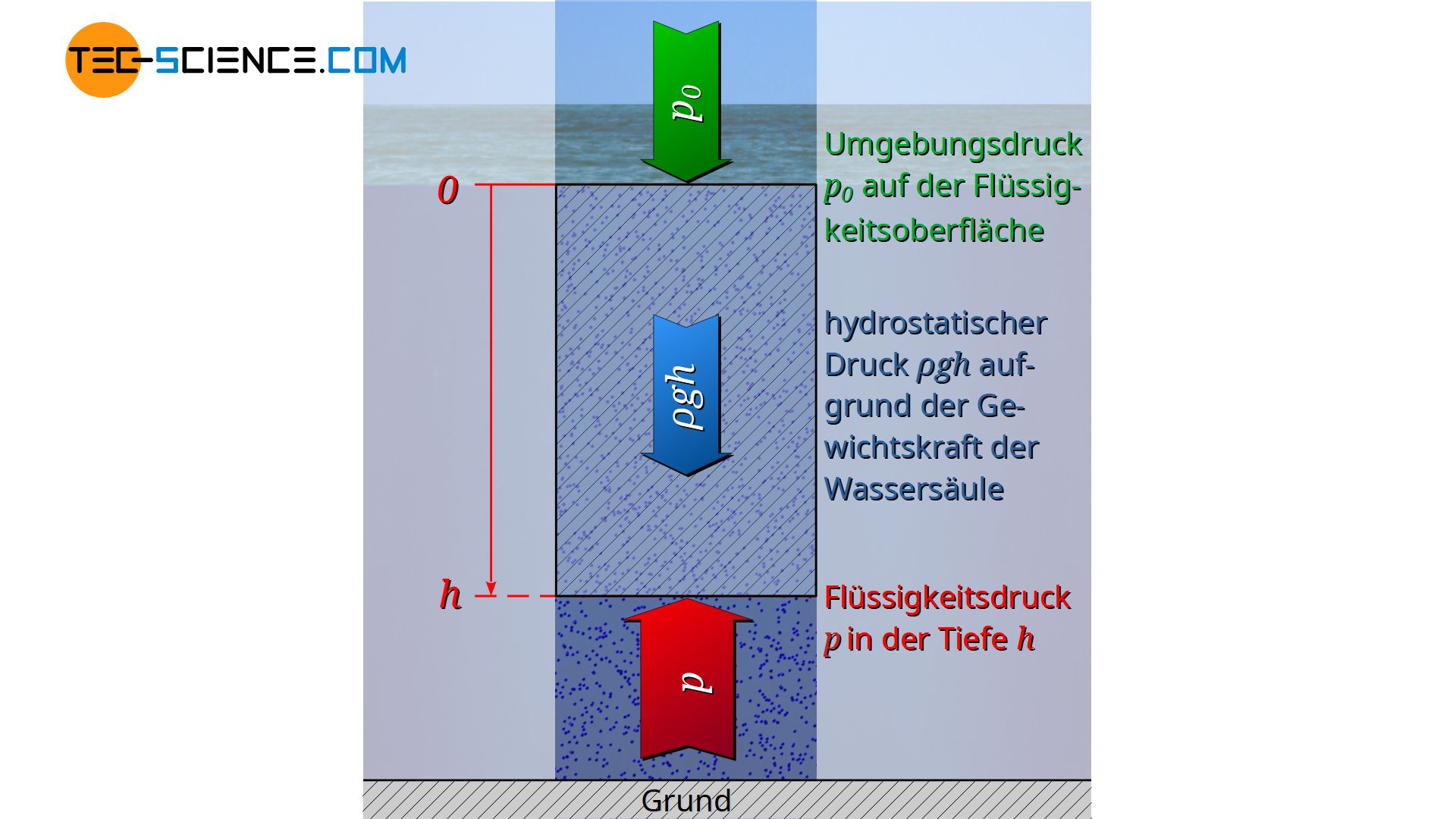
Dabei wird aus praktischen Gründen nicht mehr der Grund der Flüssigkeit als Bezugsniveau, sondern die Flüssigkeitsoberfläche genommen. Die Integrationsgrenzen ergeben sich also ausgehend der Flüssigkeitsoberfläche h=0 auf der der Umgebungsdruck p0 lastet, bis in die Tiefe h mit dem dort zu ermittelnden Flüssigkeitsdruck p:
\begin{align}
\text{d}p &= \rho \cdot g \cdot \text{d} h \\[5px]
\int_{p_0}^{p} ~ \text{d}p & = \rho \cdot g \cdot \int_{0}^{h} \text{d} h \\[5px]
\left[p\right]_{p_0}^{p} &= \rho \cdot g \cdot \left[h\right]_{0}^{h} \\[5px]
\left[p-p_0\right] &= \rho \cdot g \cdot \left[h-0\right] \\[5px]
\underbrace{p}_{\text{Gesamtdruck}} &= \underbrace{p_0}_{\text{Umgebungsdruck}} + \underbrace{\rho \cdot g \cdot h}_{\text{hydrostatischer Druck}}
\end{align}
\begin{align}
\boxed{p=p_0 + \rho g h} ~~~~~\text{hydrostatische Grundgleichung}\\[5px]
\end{align}
Die hergeleitete hydrostatische Grundgleichung besagt letztlich nicht anderes, als dass sich der Druck in Flüssigkeiten aus der Summe von Umgebungsdruck und hydrostatischem Druck ergibt.






