Erfahre in diesem Artikel mehr darüber, was ein Saugheber ist wie dieser in der Praxis funktioniert.
Einleitung
Möchte man bspw. im Sommer einen Pool über einen Schlauch entleeren, so muss nur das eine Schlauchende über den Rand in den Pool gelegt und das andere Ende außerhalb platziert werden. Das außerhalb liegende Schlauchende muss lediglich tiefer als der Wasserspiegel liegen. Wird das Wasser dann einmal angesaugt, läuft es im Folgenden permanent aus dem Schlauch. Solange das untere Ende dabei stets tiefer als der Wasserspiegel gehalten wird, wird das Wasser auch über größere Höhenunterschiede hinweg befördert, wie bspw. über den Rand des Pools (zum maximal zu überwindenden Höhenunterschied später mehr).

Anschauliche Erklärung
Dieses scheinbar paradoxe Verhalten ist dem hydrostatischen Druck geschuldet. Um dies besser zu verstehen, wird zunächst eine Plastikflasche betrachtet, die mit Wasser gefüllt ist. Am Schraubverschluss der Flasche ist ein Schlauch montiert. Wird die Flasche nun auf den Kopf gestellt, dann wird das Wasser beginnen durch den Schlauch zu fließen. Das Ausfließen des Wassers führt zu einer Vergrößerung des Volumens der Luft, welche sich in der Flasche befindet. Da aber durch den relativ kleinen Schlauch keine Luft nachströmen kann, entsteht in der Flasche ein Unterdruck.
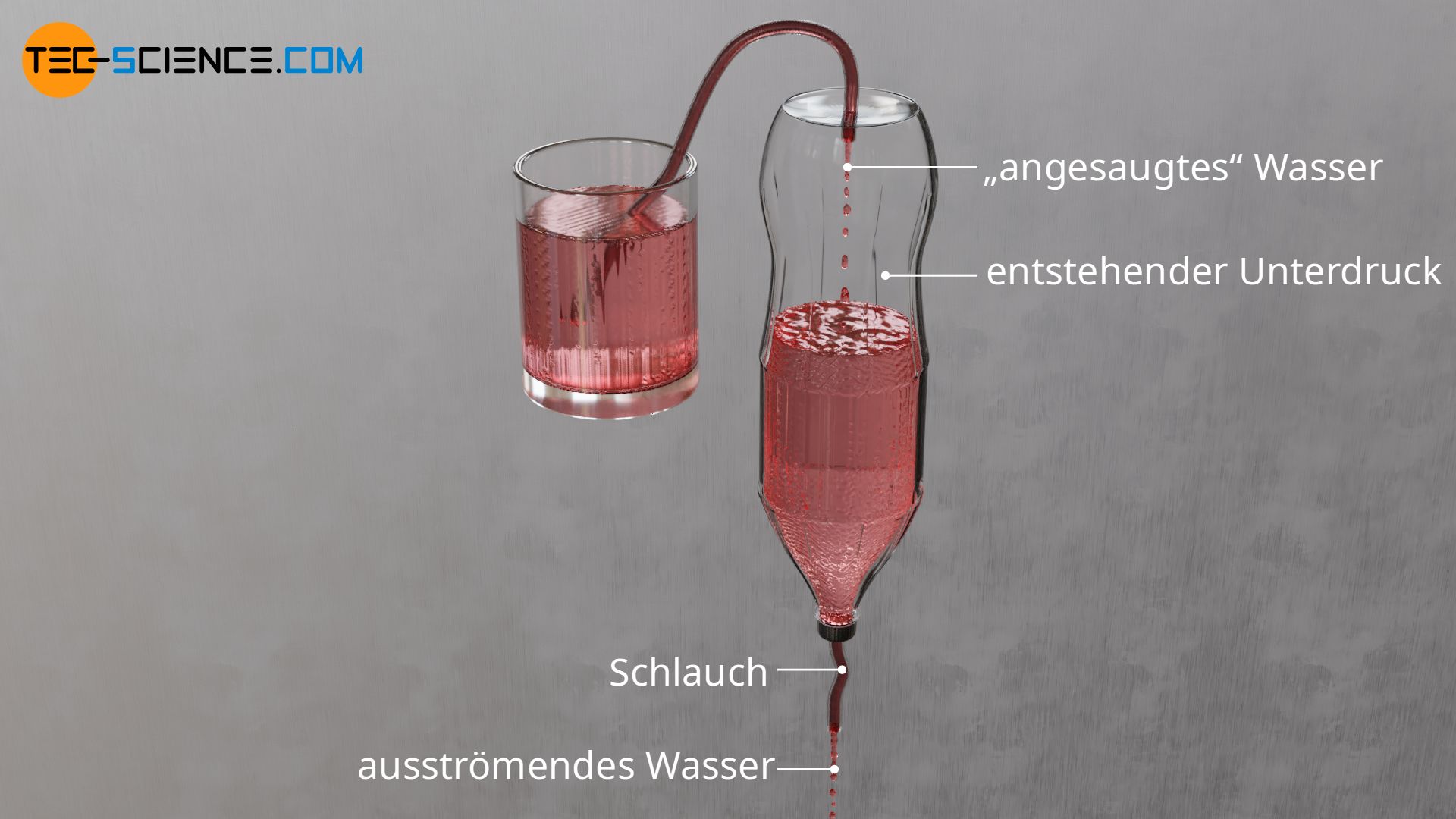
Dieser entstehende Unterdruck in der Flasche kann wiederum genutzt werden, um Wasser aus einem anderen Becken anzusaugen. Hierzu ist lediglich ein zweiter Schlauch von oben an der Flasche zu befestigen. Dieser Schlauch wird nun in das Becken gelegt, von dem das Wasser abgesaugt werden soll. Das Wasser wird sozusagen durch den Unterdruck in der Flasche angesaugt, welches durch das Abfließen des darin befindlichen Wassers erzeugt wird.
Das zu Beginn in der Flasche befindliche Luftvolumen kann prinzipiell beliebig klein gewählt werden. Schließlich kann sogar auch ganz auf ein anfängliches Luftvolumen verzichtet werden. Der erforderliche Druckgradient zur Förderung des Wassers wird sich dann direkt im Wasser bilden. Als letzten Schritt kann man anstelle der Flasche nun auch einen weiteren Schlauch verwenden. Schließlich erhält man auf diese Weise einen einzigen Schlauch, der das Wasser von einem höher gelegenen Niveau über den Scheitelpunkt saugt und dann in ein niedriger gelegenes Niveau abfließen lässt. Vorrichtungen, die diese Art der Wasserförderung nutzen, werden auch als Saugheber oder kurz als Heber bezeichnet.

An dem betrachteten Beispiel mit der Flasche wird auch anschaulich deutlich, dass die maximal zu überwindende Höhe zwischen höher gelegenem Wasserspiegel und Scheitelpunkt des Schlauches durch die maximale Saughöhe von etwa 10 Metern begrenzt ist. Denn schließlich kann als Unterdruck maximal ein Vakuum erzeugt werden. Mit einem umgebenden Luftdruck von 1 bar, kann dieser Umgebungsdruck somit maximal eine Wassersäule von 10 Metern in die Höhe drücken. Für größere Höhen reicht also der Umgebungsdruck nicht aus.
Mathematische Herleitung
Wird mit einem Schlauch Wasser von einem höher gelegenen Becken in ein tiefer gelegenes gepumpt, dann ist für den Antrieb des Wasserstroms nur der Höhenunterschied h in den Wasserspiegeln relevant. Um dies zu zeigen, wird an der höchsten Stelle des mit Wasser gefüllten Schlauchs in Gedanken ein Ventil eingebracht. Das Ventil sei zunächst verschlossen. Links und rechts des Ventils können sich somit unterschiedliche Drücke p1 bzw. p2 einstellen. Der Unterdruck an diesen Stellen führt dazu, dass der Umgebungsdruck p0 der auf der Wasseroberfläche lastet, gemäß des Trinkhalmprinzips Wasser in den jeweiligen Schlauchabschnitten nach oben drückt. Das Wasser bleibt in diesem Zustand also zunächst in den Schlauchabschnitten stehen.
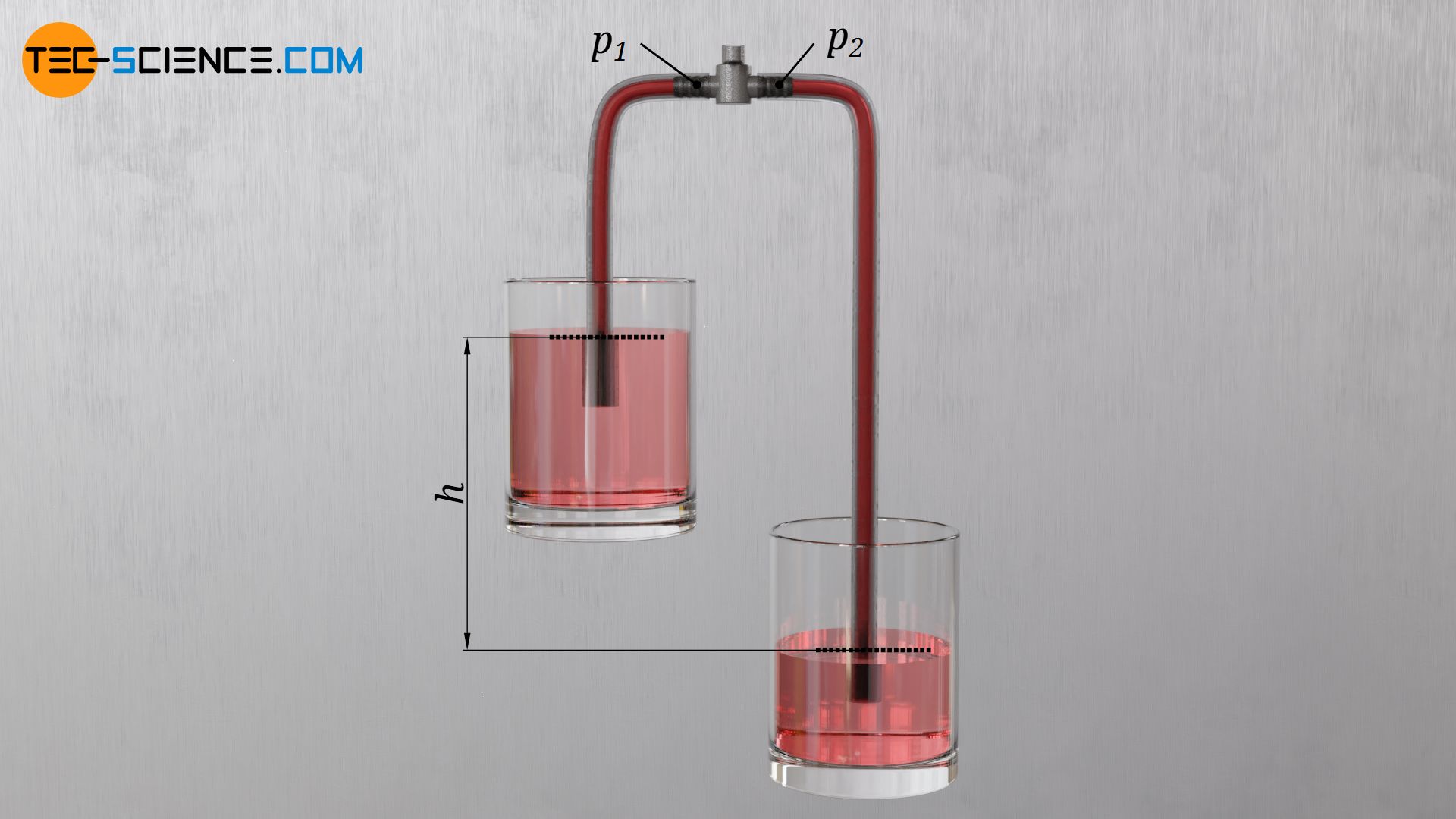
Die Eintauchtiefe der Schlauchenden in die jeweiligen Becken spielt für den Gleichgewichtszustand keine Rolle, da der hydrostatische Druck des umgebenden Wassers nach dem Prinzip der kommunizierenden Röhren das Wasser im Rohr ohnehin auf dasselbe Niveau drücken würde. Auf Höhe des Wasserspiegels wirkt also nicht nur außerhalb sondern auch innerhalb des Schlauches derselbe (Umgebungs-)Druck p0. Dieser nach oben wirkende Druck steht offensichtlich im Gleichgewicht mit dem nach unten wirkenden hydrostatischen Druck der Wassersäule im Rohr (ϱ⋅g⋅h) und dem ebenfalls nach unten wirkenden Druck p1 bzw. p2 oberhalb der Wassersäule:
\begin{align}
&p_0 \overset{!}{=} p_1 + \rho \cdot g \cdot h_1 \\[5px]
&p_0 \overset{!}{=} p_2 + \rho \cdot g \cdot h_2 \\[5px]
\end{align}
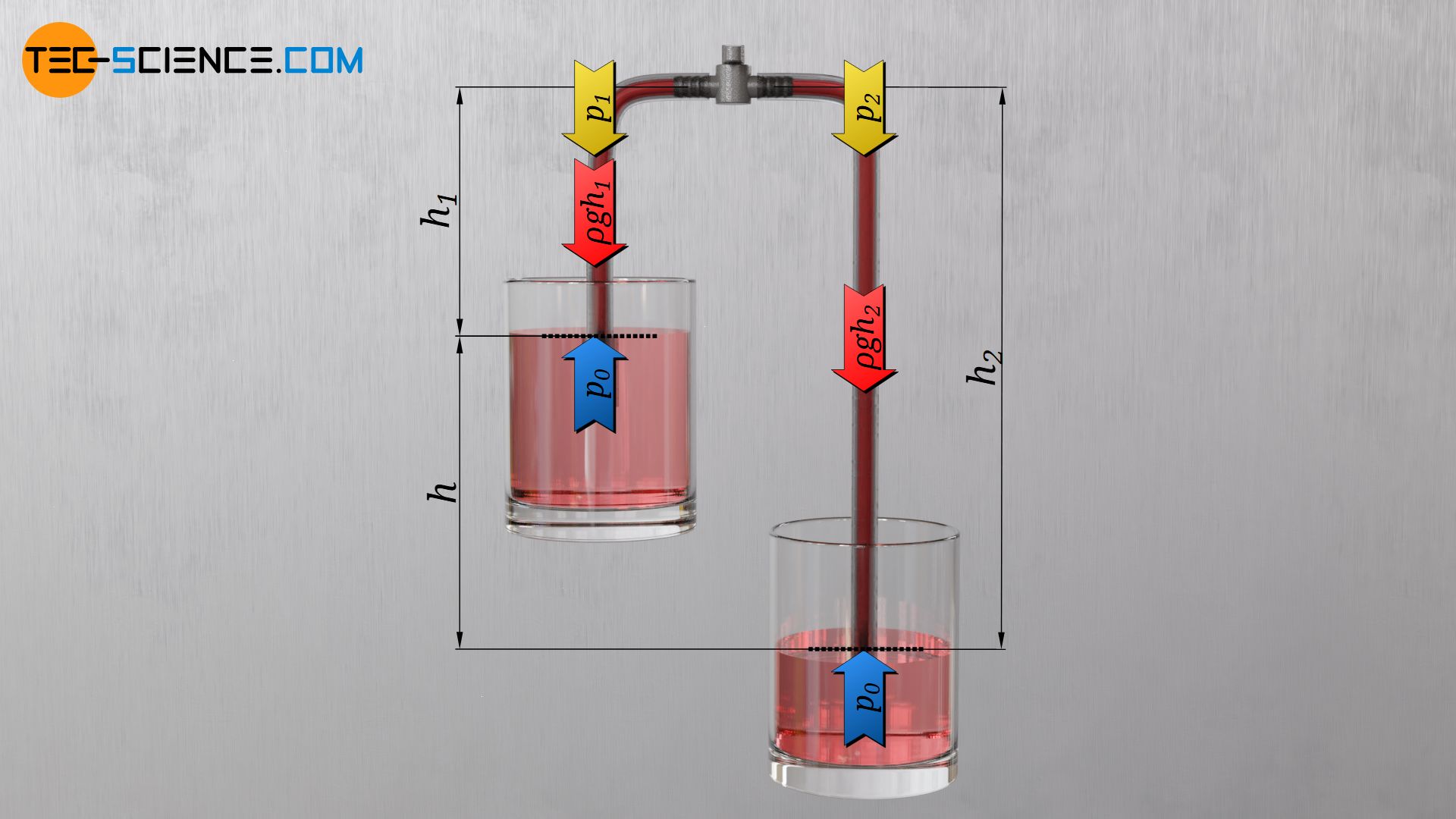
Für die Drücke links und rechts des Ventils gilt also:
\begin{align}
&p_1 = p_0 – \rho \cdot g \cdot h_1 \\[5px]
&p_2 = p_0 – \rho \cdot g \cdot h_2 \\[5px]
\end{align}
Da die Höhe h2 offensichtlich größer ist als die Höhe h1, ergibt sich auf der rechten Seite des Ventils ein geringerer Druck als auf der linken Seite. Wird das Ventil nun in Gedanken geöffnet, dann strömt das Wasser offensichtlich vom größeren Druck in Richtung geringeren Drucks. Je größer die Druckdifferenz, desto stärker wird das Wasser von von der linken Seite in Richtung rechter Seite gedrückt. Die Druckdifferenz Δp ist somit ein Maß für die Antriebsstärke des Wasserstrom. Diese Antriebsstärke ist wiederum nur Abhängig von der Höhendifferenz h der beiden Becken:
\begin{align}
\require{cancel}
\Delta p &= p_1 – p_2 \\[5px]
&= p_0 – \rho \cdot g \cdot h_1 – \left(p_0 – \rho \cdot g \cdot h_2\right) \\[5px]
&= \bcancel{p_0} – \rho \cdot g \cdot h_1 – \bcancel{p_0} + \rho \cdot g \cdot h_2 \\[5px]
\label{g}
&= \rho \cdot g \cdot h_2 – \rho \cdot g \cdot h_1 \\[5px]
&= \rho \cdot g \cdot \left(h_2 – h_1\right) \\[5px]
&= \rho \cdot g \cdot h \\[5px]
\end{align}
Wie Gleichung (\ref{g}) zum Ausdruck bringt, ist der Antrieb des Wasserstroms der Differenz der hydrostatischen Drücke in den Schlauchabschnitten links und rechts des Scheitelpunktes geschuldet. Dies wiederum ist nur auf die Höhendifferenz h in den Wasserniveaus zurückzuführen. Solange also eine Höhendifferenz zwischen oberem Wasserspiegel und unterem Wasserspiegel vorhanden ist, kann Wasser vom oberen das untere Becken gefördert werden (vorausgesetzt der Scheitelpunkt des Schlauchs liegt nicht höher als die maximale geodätische Saughöhe). Wird das geförderte Wasser nicht in ein Wasserbecken eingeleitet sondern gelangt durch das Schlauchende direkt ins Freie geleitet, dann bezieht sich die Höhendifferenz h auf das Schlauchende.
Energieerhaltungssatz
Das Saugheber-Prinzip widerspricht also nicht dem Energieerhaltungssatz, da insgesamt betrachtet Wasser von Stellen höherer potentieller Energie nach Stellen niedrigerer potentieller Energie befördert wird, auch wenn im ansaugenden Schlauchabschnitt Wasser entgegen der Schwerkraft nach oben strömt.

Man kann sich diese Situation mit einer Kette veranschaulichen, die über eine Umlenkrolle gelegt wird. Ist der Kettenabschnitt rechts der Umlenkrolle länger und damit schwerer, so bewirkt die größere Gewichtskraft, dass sich die Kette entsprechend abrollt. Nur weil dabei Kettenglieder auf der linken Seite nach oben bewegt werden, widerspricht dies auch nicht dem Energieerhaltungssatz, da sich der Schwerpunkt der Kette insgesamt nach unten bewegt.






