Die mechanische Leistung bestimmt sich über die Kraft und Geschwindigkeit bzw. über das Drehmoment und die Drehzahl.
Einleitung
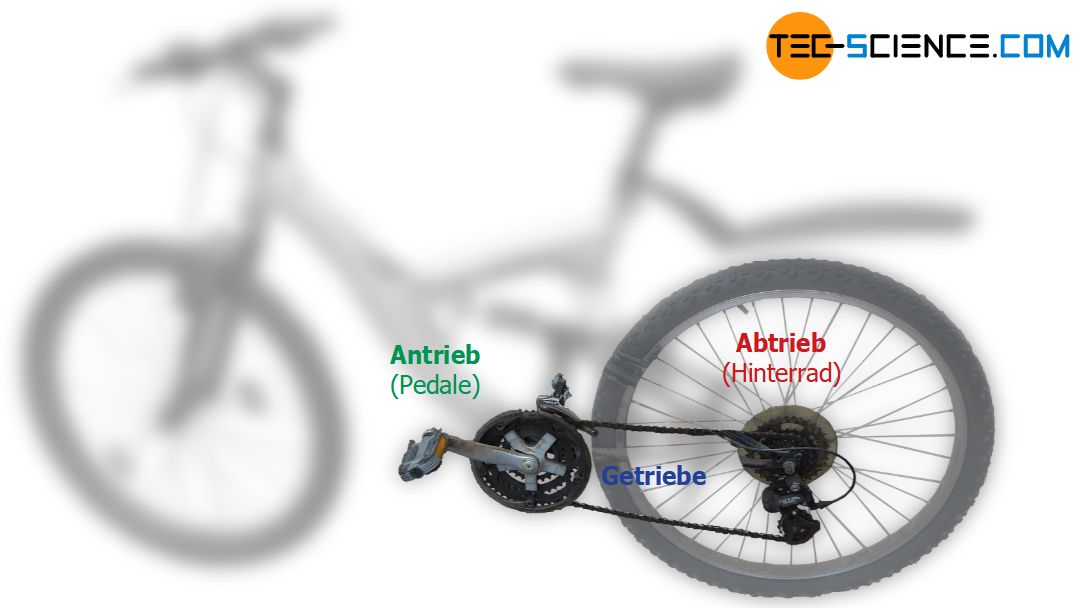
Der Begriff Leistung spielt bei Getrieben eine wichtige Rolle, da diese je nach Motorleistung entsprechend dimensioniert werden müssen. Aus diesem Grund wird in den folgenden Abschnitten zunächst auf den Leistungsbegriff näher eingegangen. Dabei scheint im Zusammenhang mit Getrieben die Frage nach der mechanischen Leistung am Abtrieb (z.B. die Abtriebsleistung am Bohrfutter einer Bohrmaschine oder am Hinterrad eines Fahrrades) immer ein Zusammenspiel zwischen zwei entscheidenden Größen zu sein. Nämlich der
- Geschwindigkeit und der Kraft bei translatorischen Bewegungen bzw. der
- Drehzahl und des Drehmomentes bei rotatorischen Bewegungen.
Die alltägliche Erfahrung zeigt dabei, dass das Getriebe bei gegebener Antriebsleistung („Motorleistung“) die eine Größe immer nur auf Kosten der anderen Größe zu ändern vermag. So wird man mit einem Fahrrad oder mit einem Auto einen steilen Anstieg – wenn also eine große Kraft erforderlich wird – nicht mit einer so hohen Geschwindigkeit im Vergleich zu einer ebenen Strecke überwinden können. Die Geschwindigkeit der angetriebenen Räder muss zugunsten der Kraft entsprechend herabgeregelt werden. Man muss sprichwörtlich „einen Gang zurückschalten“. Erst nach Überwinden des Anstieges, wenn keine große Kraft mehr erforderlich ist, kann das Fahrrad bzw. das Auto durch einen höheren Gang wieder Geschwindigkeit aufnehmen.
Auch kann unter Umständen eine Bohrmaschine, die sich im höchsten Gang befindet nicht mehr das benötigte Drehmoment entfalten, welches für das Herstellen einer großen Bohrung nötig wäre. Auch an dieser Stelle muss auf einen niedrigeren Gang zugunsten des Drehmomentes und zulasten der Drehzahl ausgewichen werden.

Definition der mechanischen Leistung
Während also eine Erhöhung der Kraft (Drehmoment) offensichtlich nur zu Lasten der Geschwindigkeit (Drehzahl) vonstatten gehen kann, hat umgekehrt eine Erhöhung der Geschwindigkeit (Drehzahl) offenbar eine unweigerliche Erniedrigung der Kraft (Drehmoment) zur Folge. Diese Sachlage ist letztlich eine direkte Folge des Energieerhaltungssatzes (mehr hierzu siehe Artikel Funktionsweise).
Um dies zu verstehen sind zunächst grundsätzliche Kenntnisse über die Begriffe Leistung und Arbeit erforderlich. Deshalb wird in den folgenden Abschnitten auf den Arbeitsbegriff bzw. auf die Leistung näher eingegangen.
Physikalisch ist die mechanische Leistung P eines bewegten Körpers ganz allgemein über die verrichtete Arbeit W und der hierfür benötigen Zeit Δt definiert:
\begin{align}
\label{def_leistung}
&P = \frac{W}{\Delta t} \\[5px]
\end{align}
Die Leistung ist also umso größer je mehr Arbeit innerhalb einer gewissen Zeit erbracht wird. Die Arbeit W wiederum ergibt sich definitionsgemäß über das Produkt aus Kraft F und Strecke Δs, entlang deren die Kraft wirkt (vorausgesetzt Kraft und Strecke sind gleichgerichtet):
\begin{align}
\label{def_arbeit}
&W = {F} \cdot {\Delta s} \\[5px]
\end{align}
Mit diesen grundlegenden Begriffen soll in den folgenden Abschnitten die mechanische Leistung bei translatorischen Bewegungen und rotatorischen Bewegungen näher betrachtet werden.
Leistung bei translatorischen Bewegungen (Linearbewegungen)
Für die Leistung von translatorischen Bewegungen (linearen Bewegungen) ergibt sich ein bestimmter Zusammenhang zwischen Kraft und Geschwindigkeit. Dies soll im Folgenden exemplarisch anhand einer Seilwinde gezeigt werden, die von einem Motor angetrieben wird.
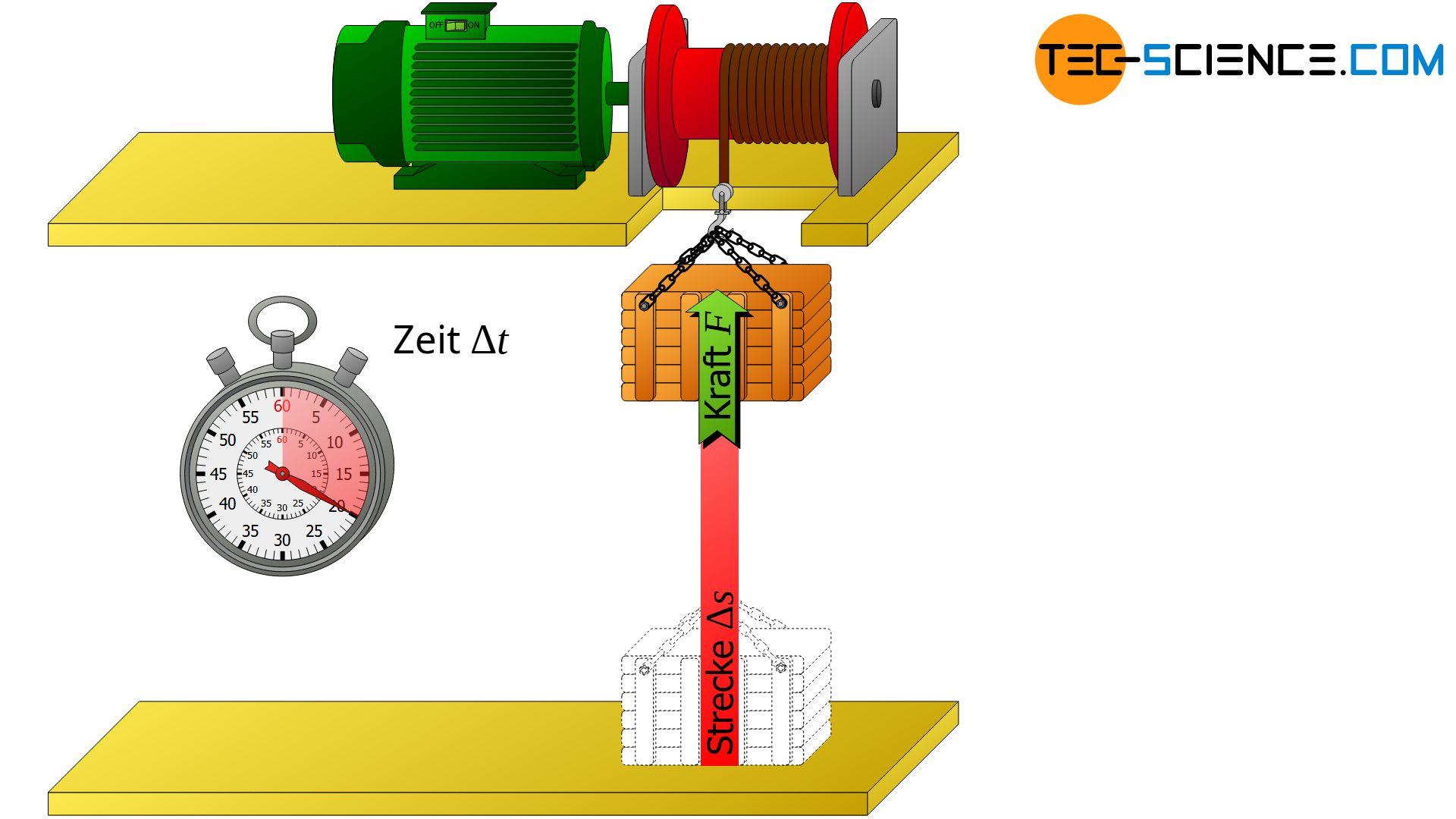
Herleitung
Die Seilwinde zieht die Kiste mit konstanter Geschwindigkeit v und konstanter Kraft F nach oben. Dabei wird die Kiste innerhalb der Zeit Δt um die Strecke Δs angehoben. Die während dieser Zeit Δt verrichtete Arbeit W der Seilwinde ergibt sich definitionsgemäß aus dem Produkt von aufgebrachter Kraft F und zurückgelegter Strecke Δs:
\begin{align}
\label{arbeit}
&W = F \cdot \Delta s \\[5px]
\end{align}
Diese Arbeit wurde offensichtlich während des Anhebens und somit innerhalb der Anhebezeit Δt erbracht. Aus der allgemeinen Definition der Leistung lässt sich dann die umgesetzte mechanische Leistung der Seilwinde P wie folgt bestimmen:
\begin{align}
\label{leistung_trans}
&P = \frac{W}{\Delta t} = \frac{F \cdot \Delta s}{\Delta t} = F \cdot \underbrace{ \frac{ \Delta s}{\Delta t}}_{=v} = F \cdot v \\[5px]
\end{align}
Bei der Umformung wurde ausgenutzt, dass der Quotient aus zurückgelegter Strecke Δs und der dafür benötigten Zeit Δt letztlich der (als konstant vorausgesetzten) Geschwindigkeit v der hochgezogenen Kiste entspricht.
Die benötigte mechanische Leistung P um ein Bauteil mit konstanter Geschwindigkeit v durch die Kraft F anzutreiben, ergibt sich aus dem Produkt beider Größen:
\begin{align}
\label{translationsleistung}
&\boxed{P = F \cdot v} \\[5px]
\end{align}
Beeinflussung der Bewegung durch ein Getriebe
Im vorliegenden Beispiel wird die geforderte mechanische Leistung vom Motor geliefert und direkt an die Seilwinde übertragen. Grundsätzlich können Motoren nicht beliebig hohe Leistungen zur Verfügung stellen. Vielmehr ist die Leistungsfähigkeit je nach Motorbauart begrenzt. Steht im Allgemeinen also nur eine bestimmte Motorleistung P zur Verfügung, so wird nach Umstellen der Gleichung (\ref{translationsleistung}) sofort ersichtlich, dass eine größere Kraft F offensichtlich nur mit einer entsprechend geringeren Geschwindigkeit v erzielen kann.
\begin{align}
\label{kraft}
&v = \frac{P}{F} \\[5px]
\end{align}
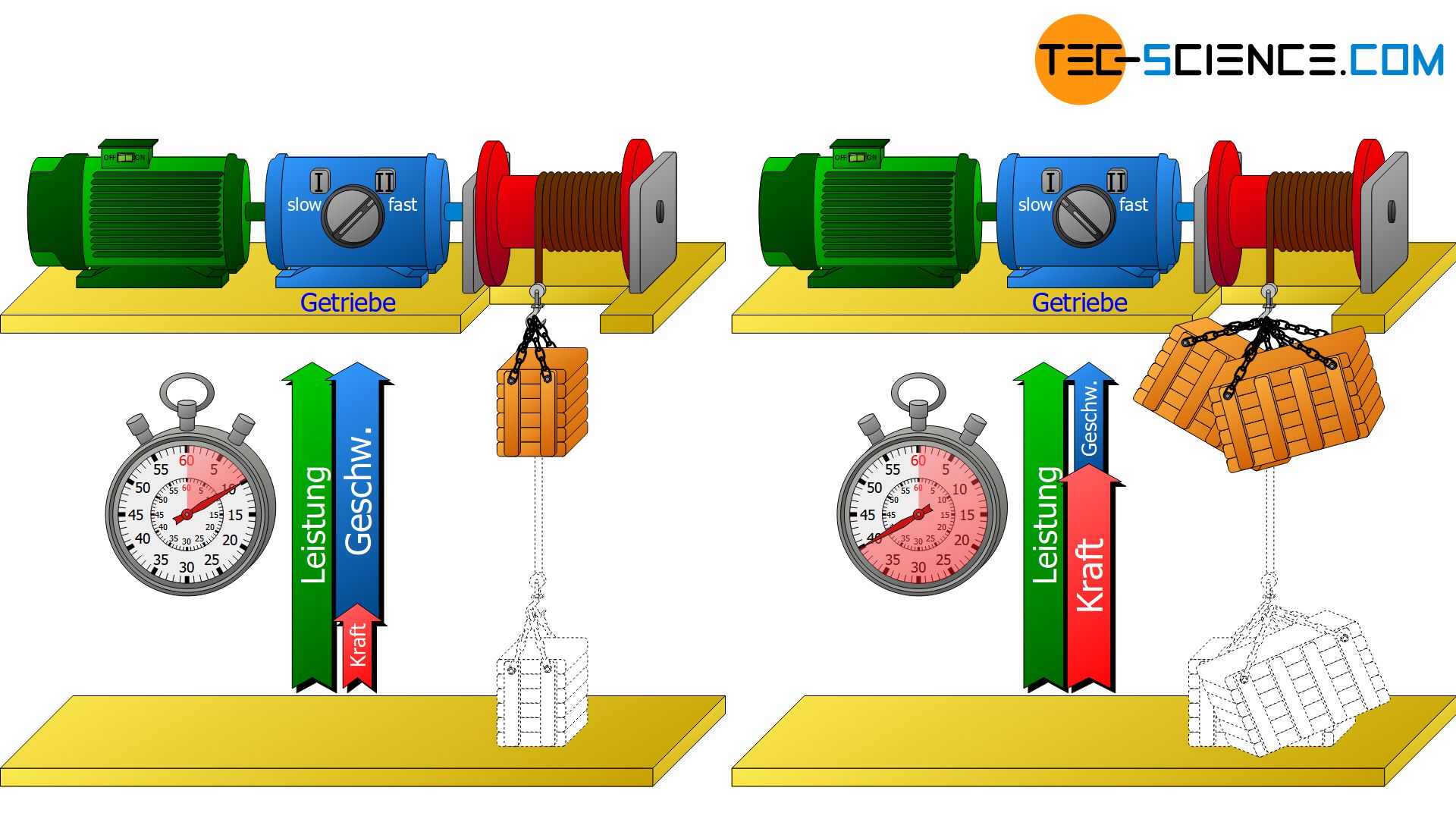
Eine schwerere Kiste kann demzufolge nur dann mit größerer Kraft angehoben werden, wenn die Geschwindigkeit entsprechend herabgeregelt wird. Umgekehrt kann bei gegebener Motorleistung Peine leichtere Kiste (wenn also nur eine geringere Kraft F zum Hochziehen erforderlich ist) mit höherer Geschwindigkeit v nach oben gezogen werden.
\begin{align}
\label{geschwindigkeit}
&v = \frac{P}{F} \\[5px]
\end{align}
Genau an dieser Stelle kommen Getriebe ins Spiel. Sie übernehmen die Steuerung der Leistung zugunsten eine größeren Kraft oder zugunsten einer größeren Geschwindigkeit. Eine Erhöhung beider Größen gleichzeitig ist folglich nicht möglich, da hierzu einer Erhöhung der Leistung erforderlich wäre. Die Leistung ist jedoch durch den Motor fest vorgegeben und kann auch durch ein Getriebe nicht geändert werden.
Getriebe ändern nicht die mechanische Leistung sondern lediglich das Geschwindigkeits-Kraft-Verhältnis, das hinter einer bestimmten Leistung steckt! Dies bedeutet entweder eine große Kraft bei geringerer Geschwindigkeit oder eine größere Geschwindigkeit bei geringerer Kraft.
Im Idealfall wird die vom Motor gelieferte Antriebsleistung PAn durch das Getriebe wieder vollständig an den Abtrieb weitergegeben (Abtriebsleistung PAb). In der Realität treten aufgrund von Reibungseffekten jedoch Leistungsverluste PV im Getriebe auf. Diese werden durch den Getriebewirkungsgrad ηG (≤ 1) ausgedrückt:
\begin{align}
\label{getriebewirkungsgrad_trans}
&\boxed{P_{Ab} = P_{An} \cdot \eta_G} \\[5px]
\end{align}
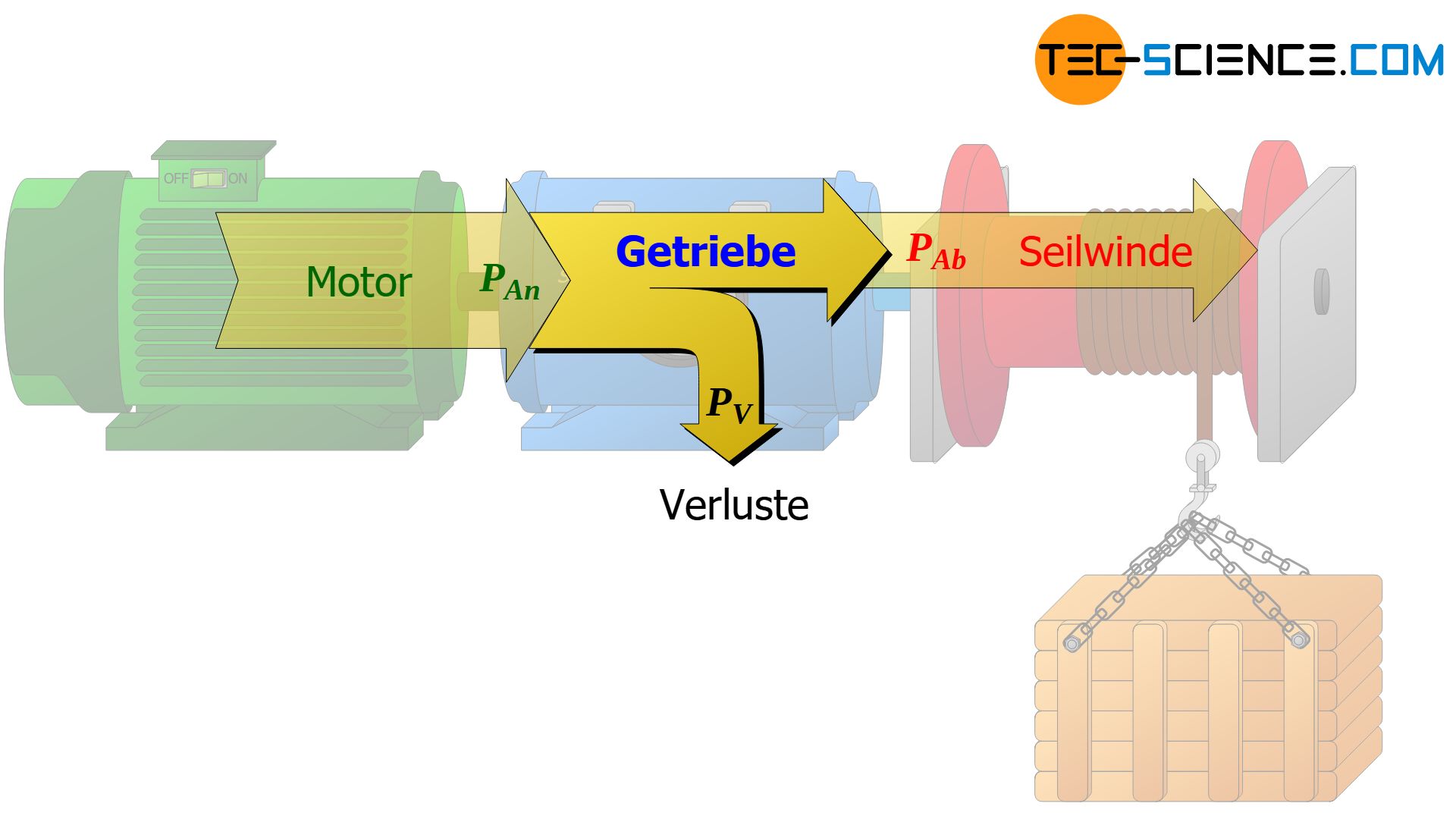
Leistung bei rotatorischen Bewegungen (Kreisbewegungen)
Die Erkenntnis über den Zusammenhang zwischen Kraft und Geschwindigkeit bei translatorischen Bewegungen lässt sich auf rotatorische Bewegungen übertragen. Hierzu wird die im Abschnitt zuvor bereits beschriebene Seilwinde nochmals betrachtet. Diesmal wird allerdings die Rotationsbewegung der Seilwinde bzw. die dabei herrschenden Kräfteverhältnisse genauer untersucht.
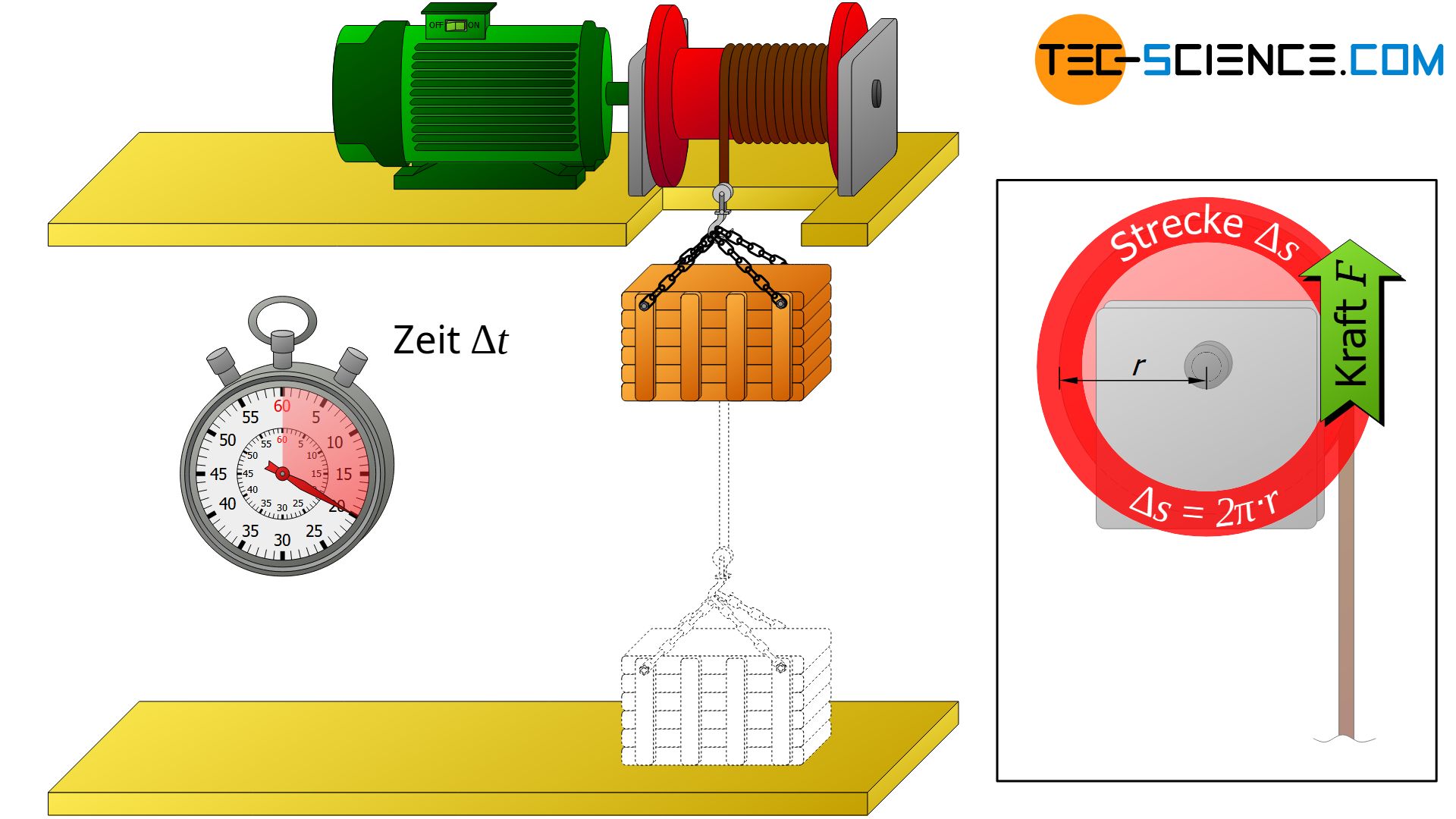
Herleitung
Die Seilwinde zieht während des Aufwickelns das Seil mit der Kraft F entlang der Bogenstrecke Δs. Die zurückgelegte Strecke Δs beschreibt diesmal allerdings keine Gerade mehr sondern einen Kreisbogen. Dabei ist jedoch die Kraft wieder in jedem Punkt stets parallel zur Strecke gerichtet. Dies bedeutet, dass die Formel für die Arbeit W=F⋅Δs wiederum ohne weiteres angewandt werden kann.
\begin{align}
\label{arbeit_01}
&W = F \cdot \Delta s \\[5px]
\end{align}
Während einer ganzen Umdrehung hat die Seilwinde dabei das Seil einmal komplett am Umfang aufgewickelt, d.h. die Kraft F wirkte entlang der Kreisstrecke Δs=2π⋅r. Die verrichtete Arbeit W der Seilwinde während dieser Umdrehung ermittelt sich dann schließlich zu:
\begin{align}
\label{arbeit_02}
&W = F \cdot 2 \pi r \\[5px]
\end{align}
Die für diese eine Umdrehung benötigte Zeit Δt wird auch Periodendauer T genannt (Periodendauer = „Zeitdauer pro Umdrehung“). Folglich wurde innerhalb der Zeit T die Arbeit W=F⋅2π⋅r verrichtet, was zur folgenden umgesetzten Leistung P führt:
\begin{align}
\label{leistung_rot}
&P = \frac{W}{\Delta t} = \frac{F \cdot 2 \pi r}{T} = 2 \pi \underbrace{\frac{1}{T}}_{=n} \cdot \underbrace{ F \cdot r}_{=M} = 2 \pi \cdot n \cdot M \\[5px]
\end{align}
Das in der Formel auftretende Produkt aus angreifender Kraft F und hierzu senkrecht gerichtetem Hebelarm r entspricht letztlich dem wirkenden Drehmoment M an der Seiltrommel, mit dem die Drehbewegung ausgeführt wird. Deshalb können beide Größe zum Drehmoment M zusammengefasst werden.
Die Formel kann noch weiter interpretiert werden, wenn man sich die Bedeutung des auftretenden Ausdrucks 1/T vor Augen führt. Während nämlich die Periodendauer T die „Zeit pro Umdrehung“ angibt, gibt der Kehrwert der Periodendauer 1/T folglich die „Umdrehungen pro Zeit“ an. Dies entspricht gerade der Drehzahl n (bzw. Drehfrequenz f) der Rotationsbewegung! Es gilt also folgende allgemeine Beziehung zwischen der Drehzahl n (bzw. Frequenz f) und der Periodendauer T:
\begin{align}
\label{drehzahl}
&n = \frac{1}{T} \\[5px]
\end{align}
Anmerkung: Grundsätzlich ist der Begriff Drehzahl (Formelsymbol n) gleichbedeutend mit dem Begriff Drehfrequenz oder kurz Frequenz (Formelsymbol f). Während der Begriff Drehzahl allerdings häufig im Zusammenhang mit der technischen Einheit „Umdrehungen pro Minute“ wiederzufinden ist, spricht man von der Drehfrequenz f meist im Zusammenhang mit der physikalischen Einheit „Umdrehungen pro Sekunde“. Beachte, dass auch wenn in der Formel das Formelsymbol n für die Drehzahl verwendet wird, grundsätzlich immer mit der Einheit 1/s zu rechnen ist!
Die mechanische Leistung P eines Bauteils, das mit konstanter Drehzahl n durch das Drehmoment M angetrieben wird, ergibt sich aus dem Produkt beider Größen; multipliziert mit dem konstanten Faktor 2π:
\begin{align}
\label{rotationsleistung}
&\boxed{P = 2 \pi \cdot M \cdot n} \\[5px]
\end{align}
Beeinflussung der Bewegung durch ein Getriebe
Die für die Rotation der Seiltrommel benötigte Leistung wird im vorliegenden Fall direkt vom Motor geliefert. Da die Leistung von Motoren jedoch begrenzt ist, können diese auch grundsätzlich kein beliebig großes Drehmoment erzeugen. Größere Drehmomente sind jedoch beim Anheben größerer Lasten erforderlich. In einem solchen Fall muss dann ein Getriebe zwischengeschaltet werden, welches bei gegebener Motorleistung P das Drehmoment M erhöht. Nach Umstellen von Gleichung (\ref{rotationsleistung}) wird dann sofort offensichtlich, dass ein höheres Drehmoment zwangsläufig eine geringere Drehzahl n zur Folge hat. Die Kiste kann nicht mehr so schnell angehoben werden.
\begin{align}
\label{getriebe}
&n = \frac{P}{2 \pi \cdot M} \\[5px]
\end{align}
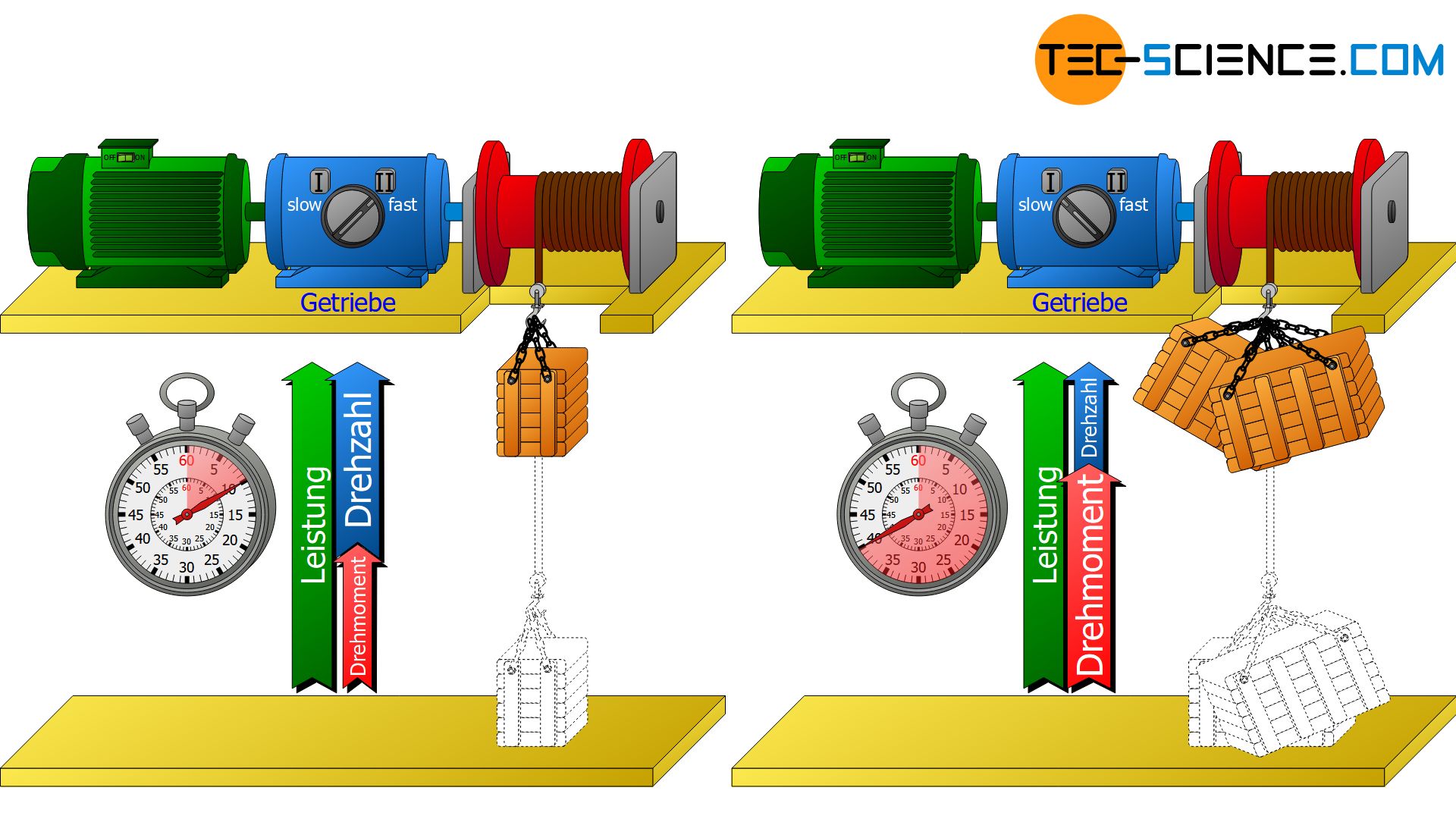
Soll hingegen eine geringe Last mit einem entsprechend verringerten Drehmoment M gehoben werden, dann kann das Drehmoment durch das Getriebe zugunsten der Drehzahl n herabgeregelt werden. In diesem Fall kann die Kiste dann schneller angehoben werden.
Beachte auch an dieser Stelle wieder, dass die Leistung P vom Motor fest vorgegeben ist und nicht durch das Getriebe geändert werden kann! Ein Getriebe kann nur das Verhältnis von Drehmoment und Drehzahl steuern! Die vom Motor gelieferte Leistung wird also durch das Getriebe nur zugunsten eines größeren Drehmomentes und damit zu Lasten der Drehzahl gewandelt (oder umgekehrt).
Getriebe ändern nicht die mechanische Leistung sondern lediglich das Drehmoment-Drehzahl-Verhältnis, das hinter einer bestimmten Leistung steckt! Dies bedeutet entweder ein großes Drehmoment bei geringerer Drehzahl oder eine größere Drehzahl bei geringerem Drehmoment.
Grundsätzlich kann durch eine größere Motorleistung natürlich gleichzeitig sowohl das Drehmoment als auch die Drehzahl erhöht werden kann. Aber schließlich wird der Motor nicht eine unbegrenzt hohe Leistung liefern können. Irgendwann ist das Leistungslimit erreicht und eine weitere Erhöhung des Drehmomentes kann schließlich nur noch durch ein Getriebe erzielt werden, was eben die besagte Erniedrigung der Drehzahl dann mit sich bringt. Außerdem macht aus wirtschaftlichen Gründen eine erhöhte Motorleistung nicht immer Sinn, da die Motoren in der Regel teurer sind als Motoren mit geringeren Leistungswerten.
Zusammenhang zwischen Translation und Rotation
An dieser Stelle soll die im vorangegangenen Abschnitt hergeleitete Leistungsformel (\ref{leistung_rot}) für Rotationsbewegungen nochmals in anderer Hinsicht interpretiert werden:
\begin{align}
&P = \underbrace{\frac{2\pi}{T}}_{= \omega} \cdot M = \omega \cdot M \\[5px]
&\boxed{P = M \cdot \omega} \\[5px]
\end{align}
Darin gibt der Ausdruck 2π/T letztlich den im Bogenmaß zurückgelegten Winkel pro Zeiteinheit an:
- volle Umdrehung = Winkel 2π
- dafür benötigter Zeit = Periodendauer T
Somit lässt sich der Ausdruck 2π/T als Winkelgeschwindigkeit ω interpretieren. Die Winkelgeschwindigkeit ω ist mit der Drehzahl n wie folgt verknüpft:
\begin{align}
\label{winkelgeschwindigkeit}
&\boxed{\omega = \frac{2\pi}{T}} = 2\pi \underbrace{\frac{1}{T}}_{= n} = 2 \pi n \\[5px]
&\boxed{\omega = 2 \pi n} \\[5px]
\end{align}
Beim Vergleich der Leistungsformeln zwischen einer Translationsbewegung und einer Rotationsbewegung zeigt sich nun eine direkte Analogie. Die analoge Größe zur Kraft bei translatorischen Bewegungen entspricht dem Drehmoment bei rotatorischen Bewegungen und die Größe der (Translations)-Geschwindigkeit entspricht der Winkelgeschwindigkeit. Das Produkt aus den jeweiligen Größen entspricht dann der Translationsleistung bzw. Rotationsleistung.
| Translationsbewegung | Rotationsbewegung | |
| „Bewegungs- stärke“ | Kraft F | Drehmoment M=F⋅r |
| „Bewegungs- schnelligkeit“ | Translations- geschwindigkeit v | Winkel- geschwindigkeit ω=v/r |
| „Leistung“ | P=F⋅v | P=M⋅ω |
Im Folgenden wird nochmals das Anheben einer Kiste mithilfe einer Seilwinde betrachtet. In diesem Fall liegt eine Rotationsbewegung der Seiltrommel und eine Translationsbewegung der Kiste vor. Beide Bewegungen sind jedoch nicht unabhängig voneinander. Wird bspw. die Rotationsgeschwindigkeit der Seiltrommel erhöht, so vergrößert sich auch die Translationsgeschwindigkeit der Kiste. Es existiert offensichtlich ein bestimmter Zusammenhang zwischen Winkelgeschwindigkeit und Translationsgeschwindigkeit.
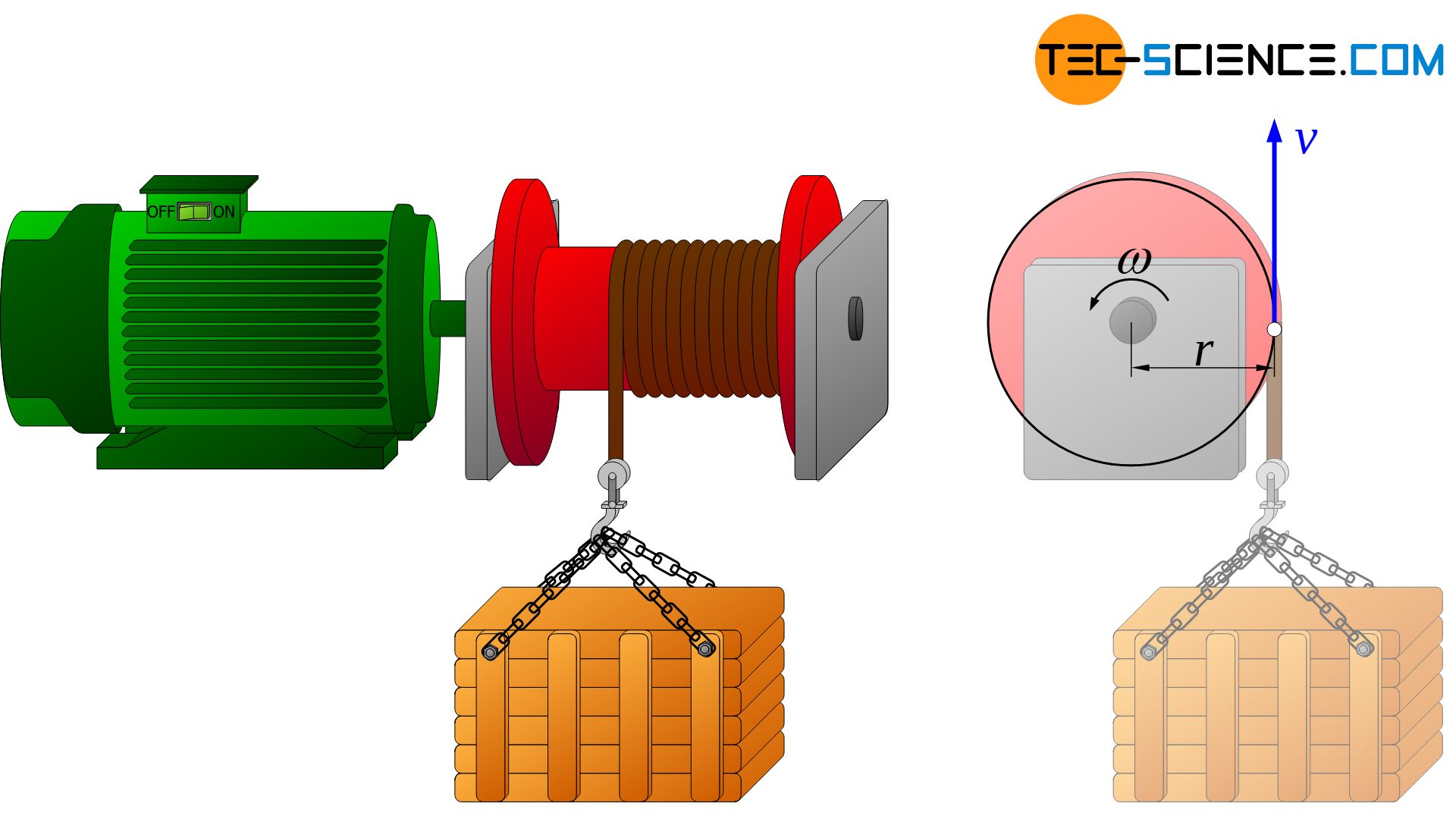
Dieser Zusammenhang kann über die Leistung hergestellt werden. So schlägt sich die Rotationsleistung PRot der Seiltrommel vollständig in Translationsleistung PTra der Kiste nieder. Setzte man die entsprechenden Formeln gleich, so gilt folgender Zusammenhang zwischen der Winkelgeschwindigkeit ω und der entsprechenden Translationsgeschwindigkeit v:
\begin{align}
\label{zusammenhang}
&P_{Tra}= P_{Rot} \\[5px]
&F \cdot v = M \cdot \omega ~~~~~\text{mit }~~~ M = F \cdot r ~~~\text{folgt:}\\[5px]
&F \cdot v = F \cdot r \cdot \omega \\[5px]
& \boxed{v = \omega \cdot r} \\[5px]
\end{align}
Die Translationsgeschwindigkeit v kann dabei als Bahngeschwindigkeit aufgefasst werden, mit der sich ein rotierender Punkt im Abstand r zur Drehachse bewegt. Ein Punkt auf dem sich aufwickelnden Seil der Seiltrommel wird mit derselben (Bahn-)Geschwindigkeit rotieren wie die Kiste hochgezogen wird. Drehmoment und Winkelgeschwindigkeit bei Rotationsbewegungen stehen somit über den Radius in direktem Zusammenhang zur Kraft bzw. Geschwindigkeit bei Translationsbewegungen (siehe Tabelle oben).
Rotation und Translation stehen über den Radius in Zusammenhang zueinander!