Buoyant forces act not only in liquids but also in gases. This will be illustrated in the following by the example of a hot air balloon.
Buoyancy
In the article Buoyancy, the physical cause of the buoyant force were explained in detail. For the sake of clarity, liquids in which the objects were submerged were considered. The magnitude of the buoyant force was determined by the volume of liquid displaced by the immersed object \(\Delta V\) on the one hand and the density of the liquid \(\rho_l\) on the other hand (with \(g\) as gravitational acceleration):
\begin{align}
&\boxed{F_b = \Delta V \cdot \rho_l \cdot g} ~~~~~\text{buoyant force} \\[5px]
\end{align}
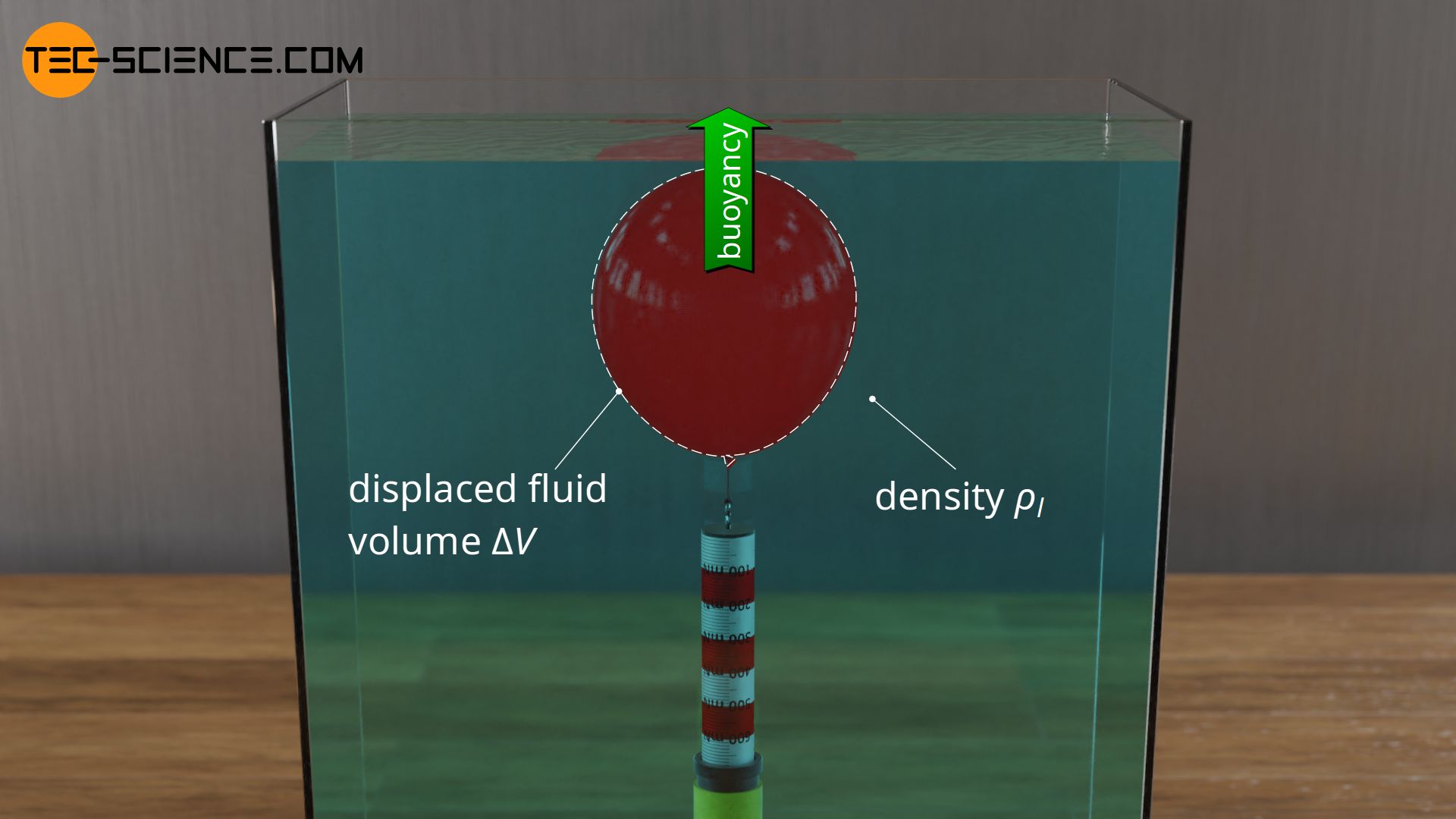
The Archimedes’ principle was also derived from this equation, which states that the buoyancy of a body is equal to the weight of the displaced liquid. For this purpose, in the equation above, the product of the displaced liquid volume and the liquid density can be interpreted as the displaced liquid mass \(\Delta m\). The product of mass and gravitational acceleration then shows up as the weight of the displaced liquid \(F_{g,dis}\):
\begin{align}
&F_b = \underbrace{\Delta V \cdot \rho_l}_{\Delta m} \cdot g \\[5px]
&F_b = \underbrace{\Delta m \cdot g}_{F_{g,dis}} \\[5px]
&\boxed{F_b = F_{g,dis}}~~~~~\text{Archimedes’ principle} \\[5px]
\end{align}
From liquids to gases
In principle, one can now also imagine a liquid whose density becomes smaller and smaller in thought. At some point one will have finally approached the density of gases. So there is no reason why buoyancy should not also occur in gases. And indeed, practice shows that buoyant forces also act in gases. These are calculated with the same equations as for liquids. The density \(\rho_l\) therefore generally refers to the density of the surrounding fluid (whether liquid or gas).
The calculation of the buoyant force in gases is usually easier compared to liquids, since a body is usually completely submerged in the gas. The displaced gas volume thus corresponds to the volume of the body. With liquids, on the other hand, it must be noted that they can only be partially submerged in the liquid. The displaced liquid volume then corresponds to the actually submerged body volume.
Since gases have relatively low densities compared to liquids, the displaced gas mass into which a solid object is immersed is often negligibly small compared to its own mass. In such a case, the buoyancy can usually be neglected compared to the weight of the body. For example, a person displaces about 80 litres of air by his own body volume. With an air density of approximately 1.25 gram per litre, the displaced air mass is thus 100 g. A person with a mass of 80 kg thus appears to be 100 g lighter due to the buoyancy caused by the surrounding air (this corresponds to only about 0.1% of the body weight).
However, in cases where the weight of a body is relatively small compared to its volume, the buoyancy also plays an important role in gases. This will be especially the case when two gaseous substances are considered. Party balloons filled with helium are a typical everyday example of this, in which the buoyancy of the surrounding air causes the balloon to rise.

In this case, the helium mass inside the balloon is lighter than the displaced air mass, so that in accordance with the Archimedes’ principle, the resulting buoyancy is greater than the weight of the helium. This buoyant force is so great that it lifts not only the weight of the helium but also the weight of the balloon and the cord. Over time, however, the helium will leak from the balloon and the balloon will shrink. At some point the buoyancy will only be sufficient to keep the balloon floating but no longer make it rise. In this case, the buoyancy is equal to the weight of helium plus that of the balloon (and the cord). If even more helium leaks, the volume of the balloon will eventually be so small that significantly less air mass will be displaced. The buoyancy decreases according to the Archimedes’ principle. Finally, the buoyancy can no longer balance the weight of the helium and that of the balloon and the balloon sinks to the ground.
Hot air balloon
Hot air balloons use the same principle of buoyancy. Instead of helium, heated air is used. A hot air balloon consists of a airtight bag (called envelope) consisting of several segments sewn together. The basket is attached to the lower end of the balloon with suspension ropes. The burners, which are fed by gas cylinders, are mounted on a frame.

Typical specifications of a hot air balloon are given in the figure below, which illustrates how it works. The envelope of the balloon has a volume of about 4000 m³. This means that the balloon displaces a volume of 4000 m³ of cold atmospheric air. At an ambient temperature of about 24 °C, the air has a density of about 1.17 kg/m³. With a volume of 4000 m³, the balloon thus displaces a cold air mass of about 4700 kg. According to the Archimedes’ principle, this results in a buoyant force of 47 kN. If the same air were inside the balloon as outside, then of course there would be an air mass of 4700 kg inside the envelope. The buoyancy would then correspond to the weight and the air would practically float inside the balloon, but would not generate any effective upward force.

Therefore, the air inside the balloon is heated to over 100 °C with burner flames. As a result, the air density drops and with it the air mass inside the balloon. The decrease of the air mass inside the balloon can be explained by the fact that the heated air expands and partly flows out of the balloon. Unlike a party balloon, a hot air balloon is not a closed system, but open at the bottom, where the gas burner heats the air (and also open at the top, more about this later). Note that the volume of the balloon practically does not change during heating, so the displaced air mass or the associated buoyant force does not change either.
At an internal air temperature of 104 °C, for example, the density of the air has dropped to about 0.92 kg/m³, so that inside the balloon volume of 4000 m³ there is only an air mass of approx. 3700 kg. The buoyancy of 47 kN is now only countered by a weight of 37 kN. Thus the heated air generates an upward force of 10 kN. This is sufficient to lift a total mass of 1000 kg! The envelope with about 150 kg and the burner as well as the gas bottles with a total of 250 kg have to be taken into account. After deducting a basket mass of 100 kg, this leaves 500 kg for transporting the passengers.
Since the buoyancy of a hot air balloon is determined by the displaced air mass (i.e. by the balloon volume) and can practically not be changed during the flight, the air mass in the balloon must be increased in order to descent the balloon. This is achieved by a hole on the top of the balloon, which is closed during ascent and can be opened with a rope to allow the balloon to sink. This causes the hot light air to escape upwards and cold heavy air to flow in from below. The air mass inside the balloon increases again and the weight is greater than the buoyancy, so that the hot air balloon now sinks downwards.
Outlook
In the article Buoyancy, the cause of buoyant forces in liquids was explained by the different hydrostatic pressures on the bottom or top of the submerged object. The fact that buoyant forces also act in gases suggests that there must also be something like “hydrostatic” pressures in gases. In the same way as the pressure in liquids increases with increasing depth, the pressure in gases should also increase with increasing depth or decrease with increasing height. And in fact this is exactly the reason why the atmospheric air pressure decreases with increasing altitude – for example on mountains. More information can be found in the article Barometric Formula.