Important lattice structures are the face-centered cubic (fcc), the body-centered cubic (bcc), and the hexagonal closest packed (hcp).
Introduction
The article on lattice structure of metals explains why the atoms in a metal are arranged with a certain regularity and thus form a lattice structure. Only in rare cases does a simple cubic crystalline structure appear, as shown in the animation below.
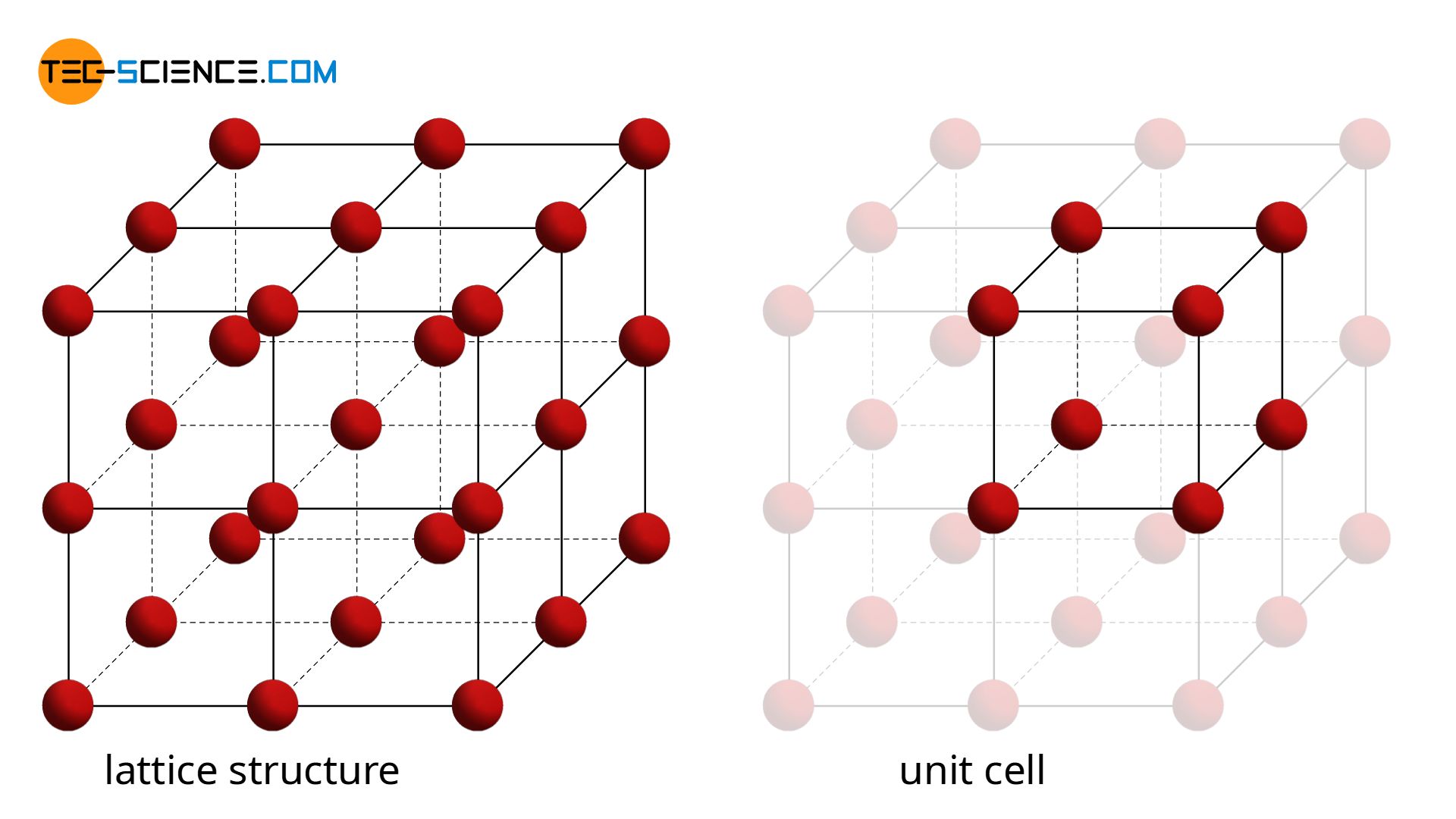
Of much greater technical importance are variations of this simple cubic lattice structure. These include the body-centered cubic lattice (bcc) and the face-centered cubic lattice (fcc), as well as the hexagonal closest packed lattice (hcp).
The difference in the lattice structure has in particular strong effects on the ductility of the respective metals! While the fcc-lattice shows the highest ductility and the hcp-lattice the lowest deformability, the bcc-lattice has a malleability that lies between the other structures.
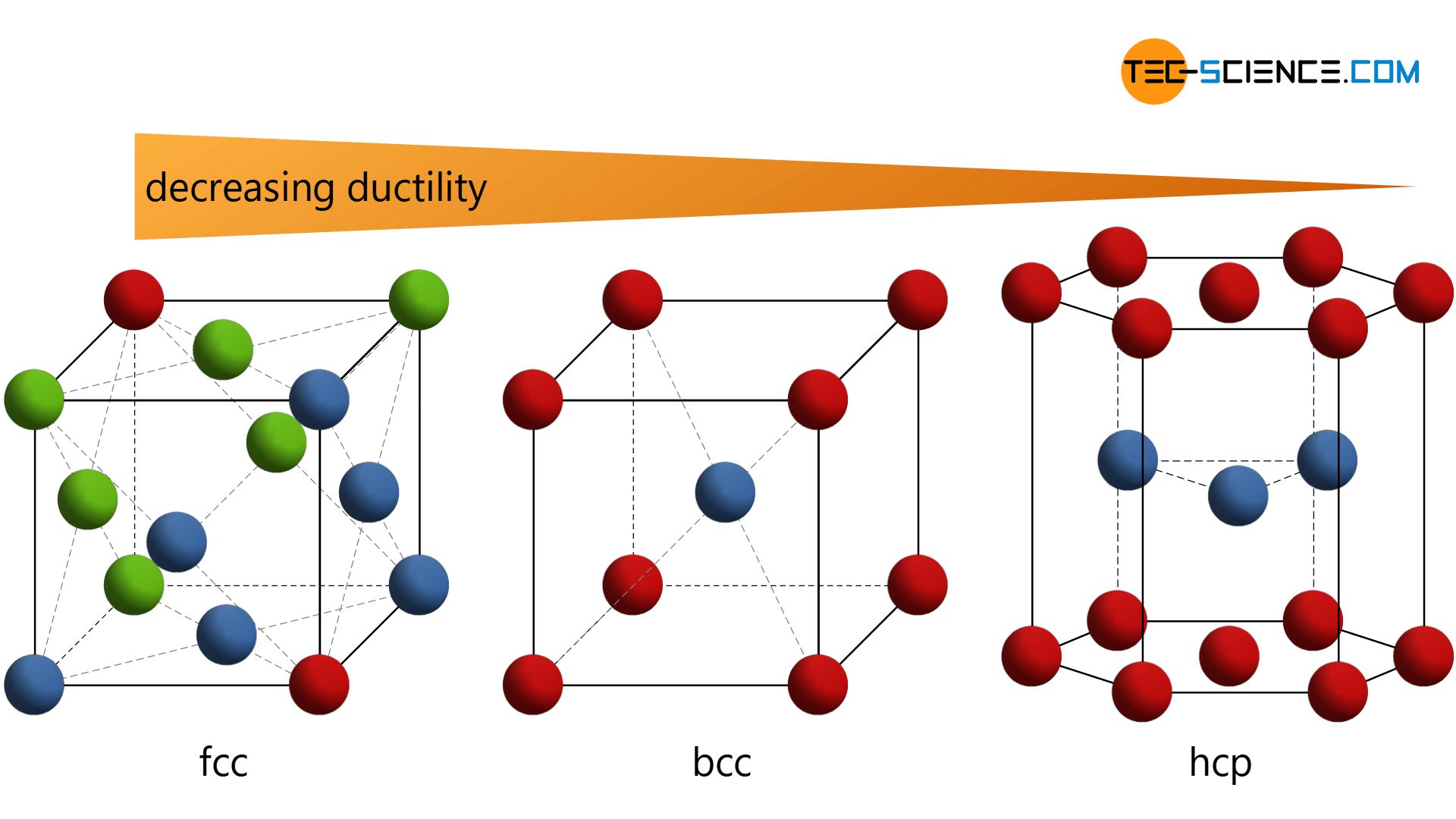
In order to be able to understand these differences in ductility, it is first necessary to understand the structure of the different types of lattice. For this reason, this article discusses the realization of the three most important lattice types.
Body-centered cubic lattice structure
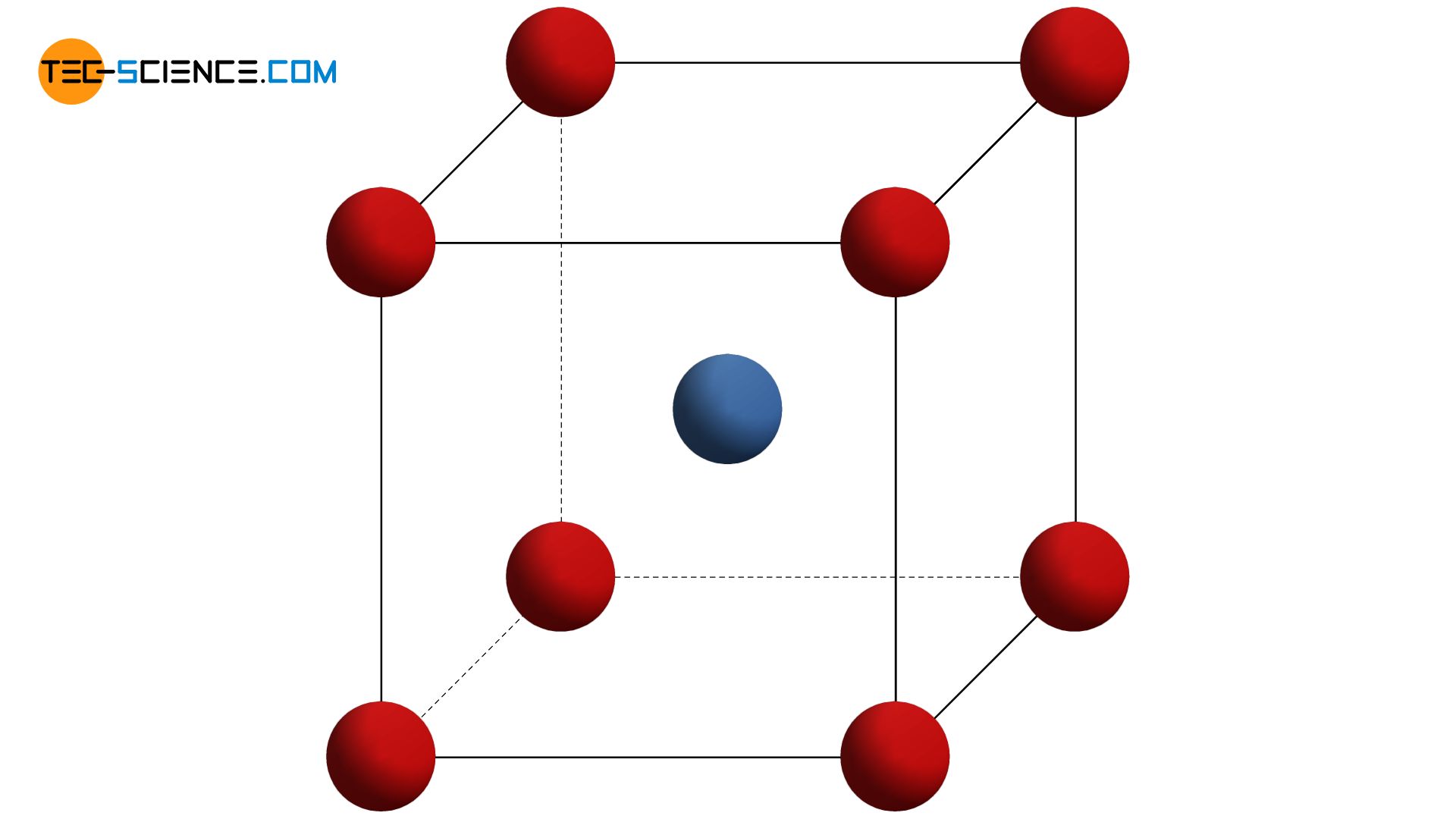
A variation of the primitive cubic lattice is the so-called body-centered cubic lattice structure (bcc). In this atomic structure, the individual planes of atoms (lattice plane) lie in the gaps of the respective lower planes of atoms. As with the primitive cubic lattice, the unit cell also has the basic shape of a cube. In addition to the corner atoms, which each sit in the corners of the cube-shaped unit cell, there is now another atom centered in the middle of the cube (“body”).
The body-centered cubic lattice structure (bcc) contains another atom in the middle of the cube-shaped unit cell next to the corner atoms!
Typical representatives of suchbody-centered cubic structures include the metals iron, chromium, molybdenum, vanadium and tungsten.
In the body-centered cubic crystal, one atom is in direct contact with eight surrounding atoms. This number of direct neighbor atoms is also called coordination number. The coordination number in the bcc lattice is consequently 8. In the simple cubic lattice, on the other hand, a coordination number of 6 is obtained.
The coordination number describes the number of directly adjacent atoms!
For the representation of unit cells, it makes sense to draw the atoms downsized, even if they “touch” in reality. In order to clarify the spatial arrangement of the atoms, it is also common to indicate the basic form of the unit cell by dashes. Note, that these lines do not represent binding forces!
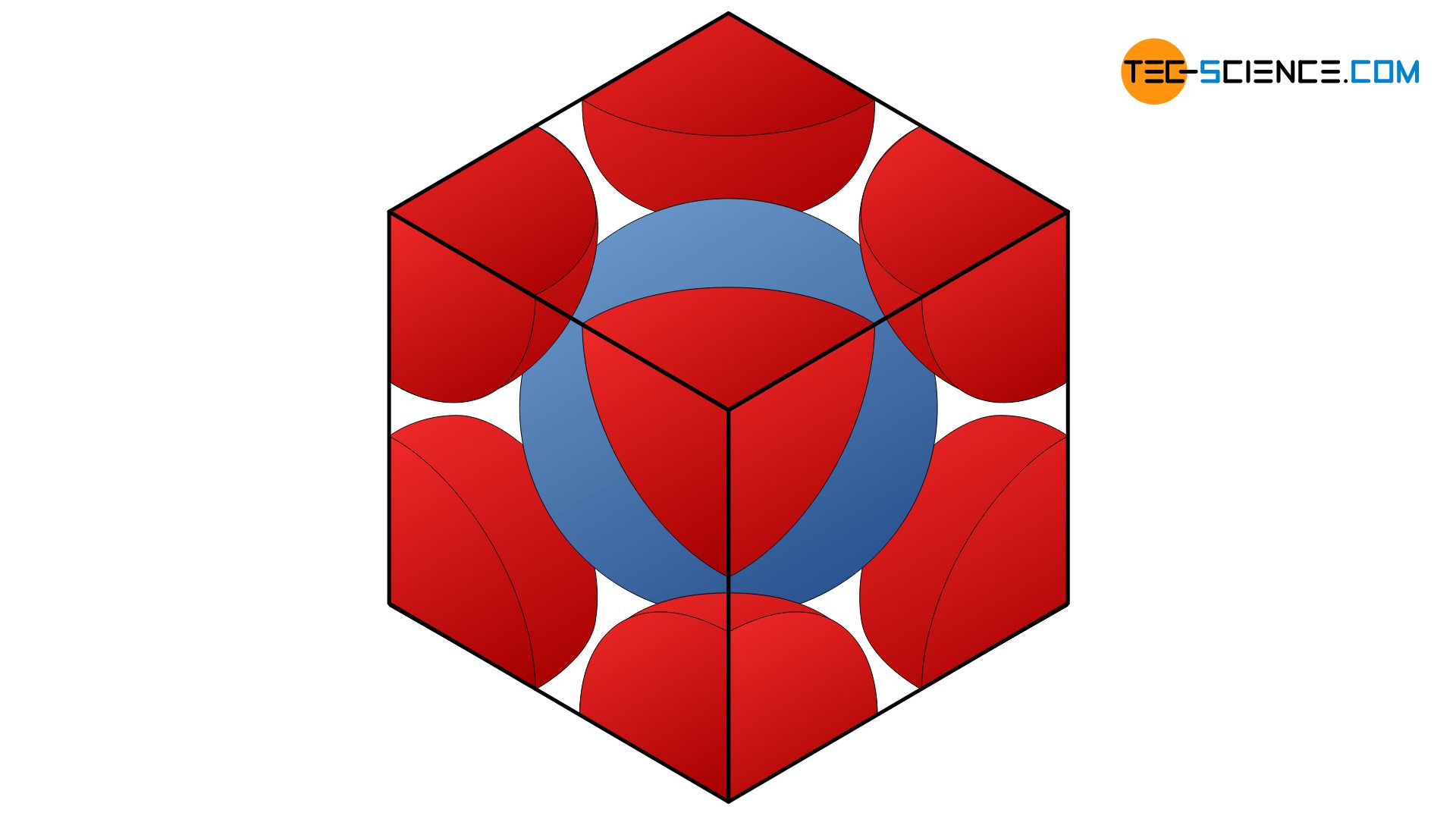
If the atoms are realistically regarded as touching spheres, the so-called packing density of an atomic structure can be determined (also referred to as packing factor). The packing density indicates what percentage of the unit cell is filled with atoms. For the body-centered cubic lattice, a packing density of 0.68 can be determined in this way. This means that 68 % of the total lattice volume (or unit cell) is occupied by atoms. The remaining 32 % are attributable to the “gaps” between the atoms. The derivation of this packing density is shown in a separate post.
The packing density (or packing factor) is the ratio of the atomic volume to the total volume of the unit cell!
Hexagonal closest packed lattice structure
In the body-centered cubic crystalline structure, the superposed atomic planes have gaps so that the respectively underlying plane fits exactly into the gaps of the upper one. The atomic levels are thus not maximally packed. The situation is different with the hexagonal lattice structure.
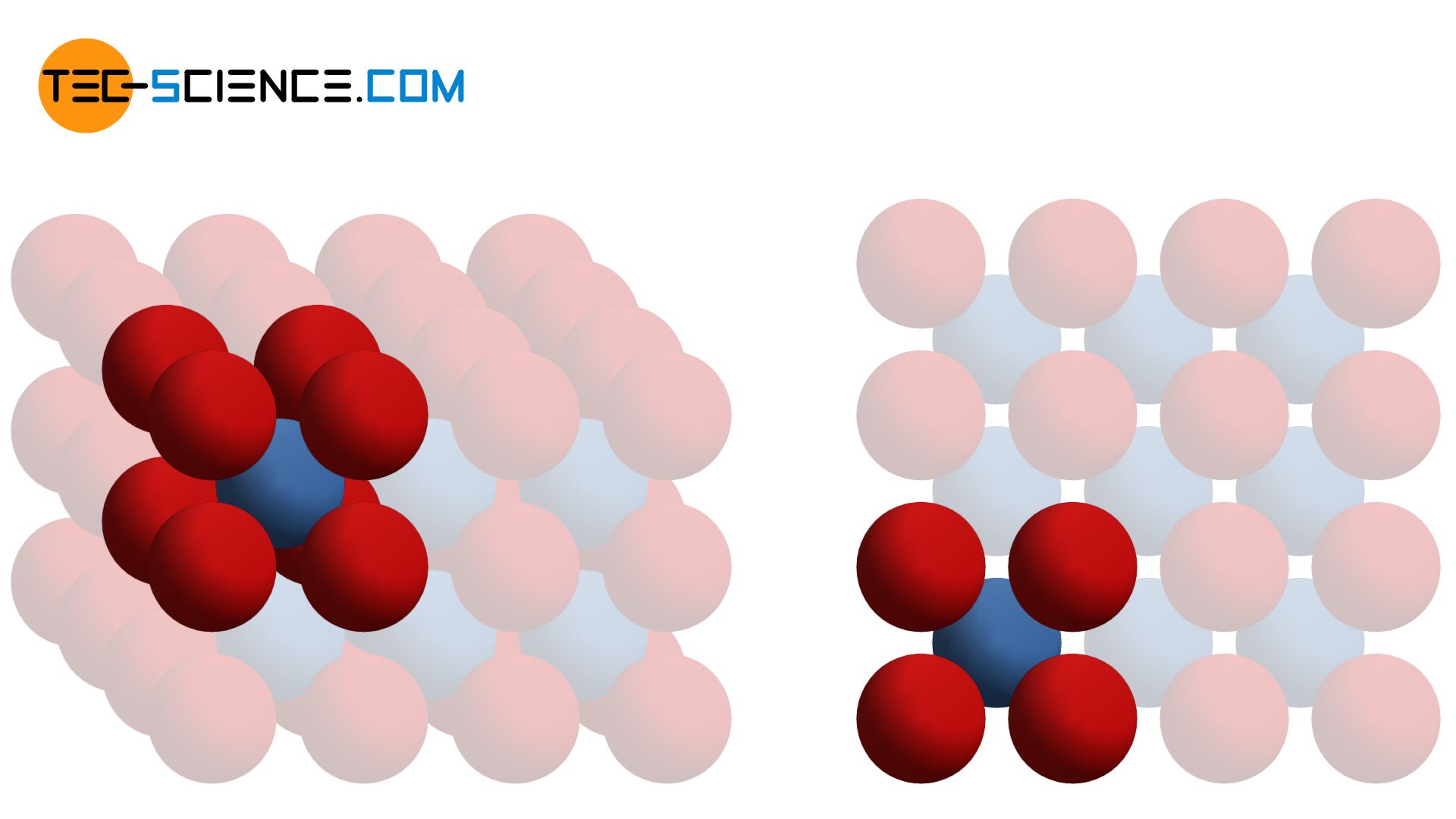
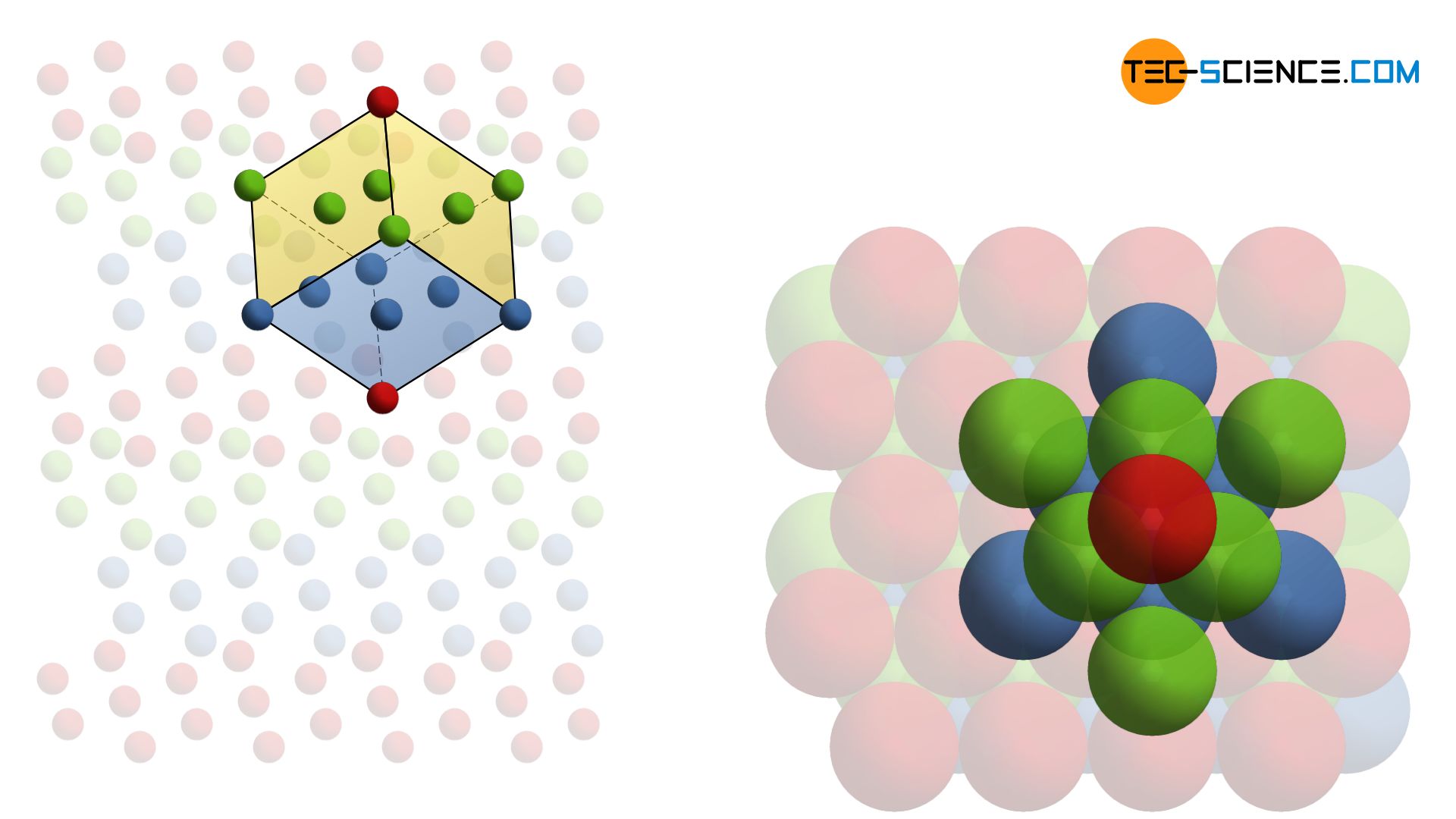
In the hexagonal structure, the atoms of a lattice plane are densely packed together. A single atom in this lattice plane A (shown in red) is always touched by a total of six neighboring atoms. The overlying atomic plane B (shown in blue) is constructed identically in principle. However, it is just so shifted that the atoms of this plane fit exactly in the indentation of the underlying plane. An atom of the upper lattice plane thus sits in the gap formed by three atoms of the lower layer. This lattice plane sequence AB (also called stacking sequence) is now repeated continuously (ABAB …).
Stacking sequence is the order of the permanently repeating atom layers!
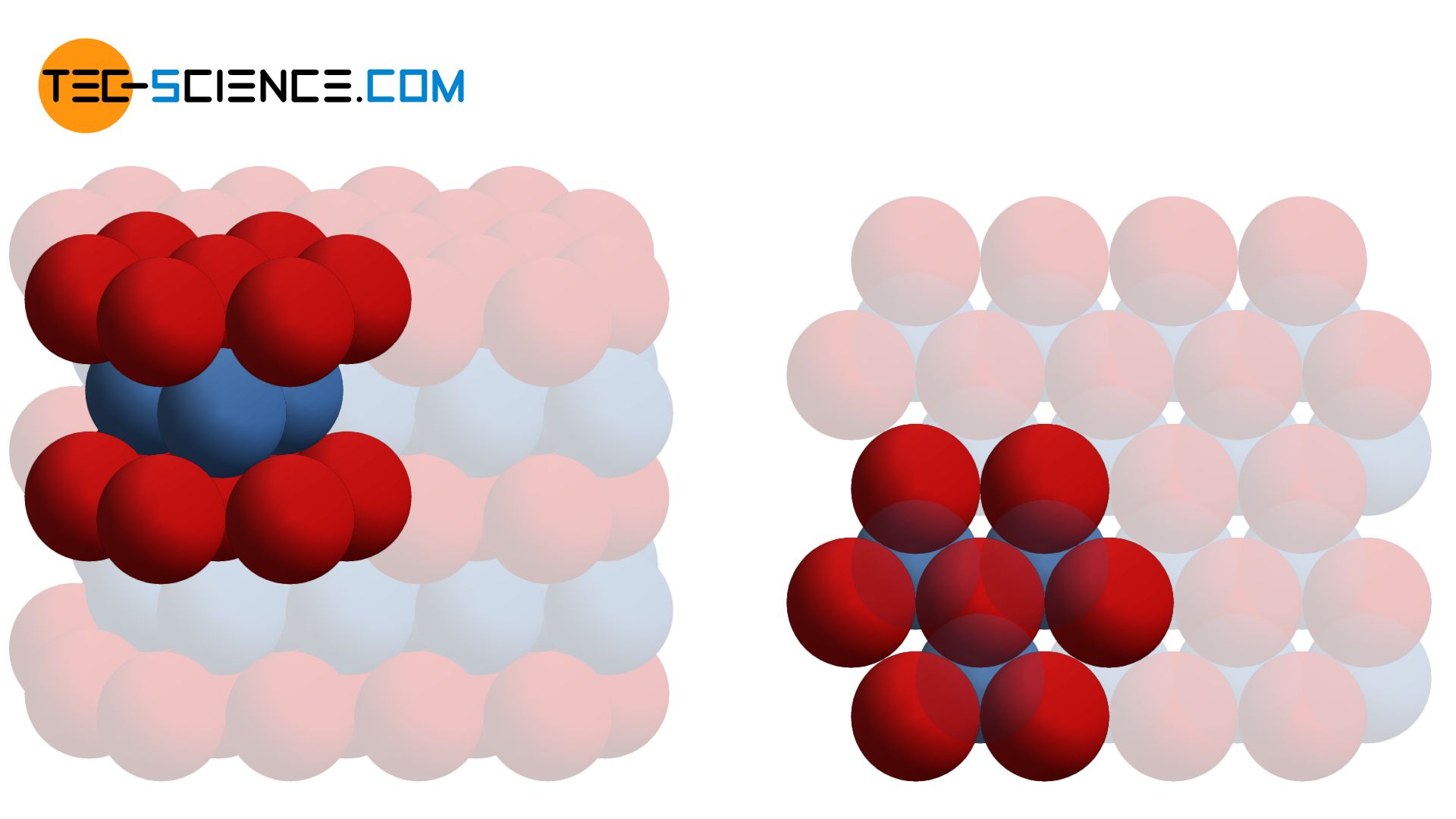
The metals titanium, cobalt, zinc and magnesium typically occur in such a hexagonal lattice structure with maximum packing density. An atom in the hexagonal closest packed lattice is surrounded by 12 direct neighboring atoms. The coordination number in this type of lattice is therefore 12.
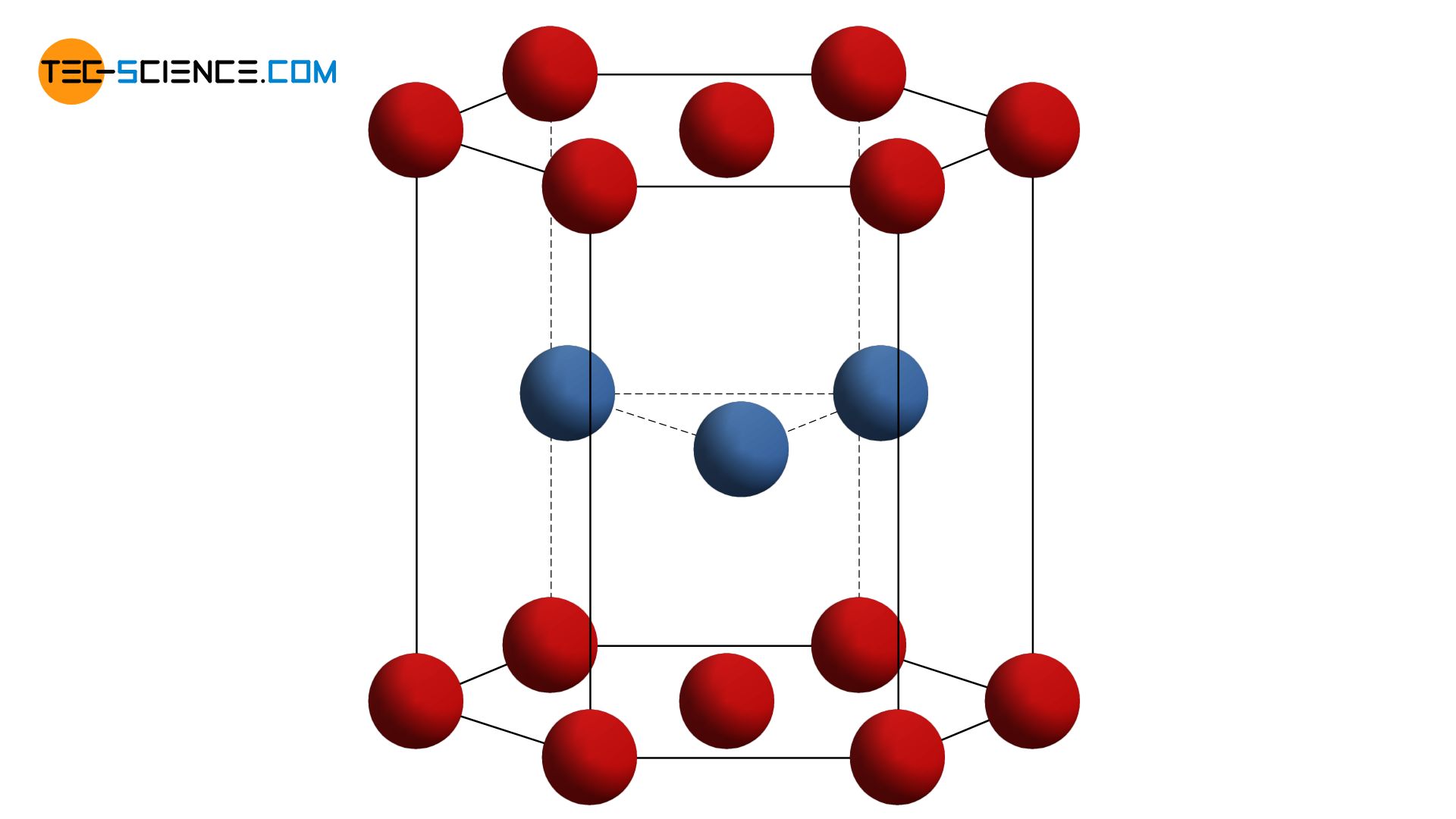
The unit cell of a hexagonal closest packed lattice can be reduced to a hexagonal base area. In the middle of the unit cell are three other atoms that sit in the resulting atomic gaps of the base and top surfaces. Since the individual atomic levels that make up the structure are maximally packed, we also speak of closest packed atomic planes. Consequently, the lattice is referred to as a hexagonal closest packed lattice structure (hcp).
In the hexagonal closest packed lattice, two atomic layers with a hexagonal base form the shape of the unit cell. In the middle of the base areas is another atom, as well as a total of three other atoms in the middle of the unit cell!
The packing density of the hcp-lattice corresponds to the maximum possible packing density of 74 %. This maximum packing density is generally applicable to any spherical body.
For spherical bodies a packing density of 74 % can be reached at maximum!
The addition of “closest packed” in the name of the hexagonal lattice already implies that there are also other hexagonal lattice structures. For example, graphite also has a hexagonal lattice structure (hex), but this is not closest packed as in the hcp-lattice.
While in a atomic plane of the hcp-lattice an atom is directly surrounded by 6 other atoms, in the hexagonal lattice of graphite there are only three neighboring atoms. The individual atomic layers are arranged with an offset and can be relatively easily shifted against each other. The shifted atomic planes can thereby be detached relatively easily. For example, this process uses a graphite pencil when drawing on a sheet of paper.
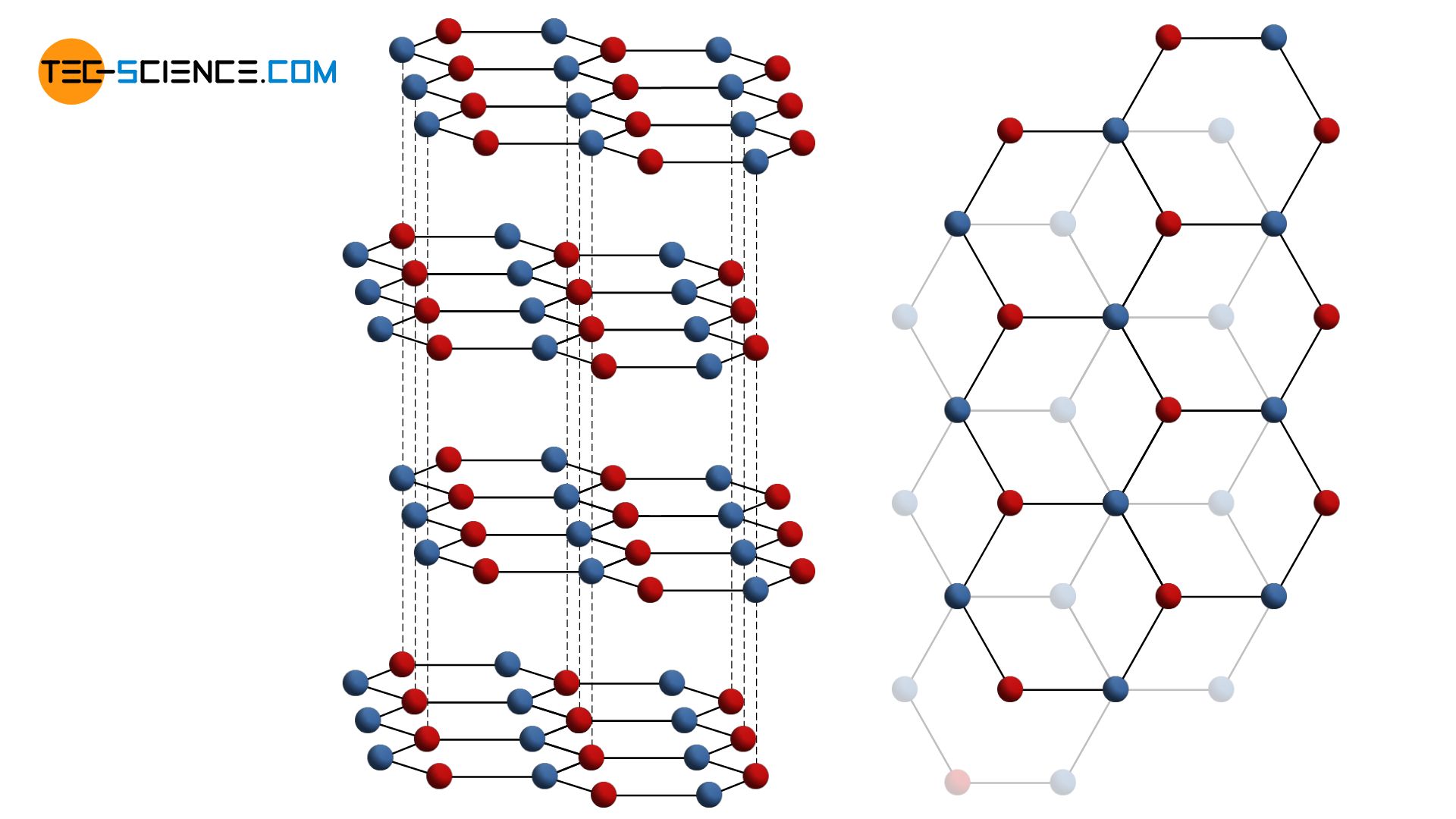
Face-centered cubic lattice structure
As well as the hcp-lattice, the face-centered cubic lattice structure (fcc) has maximum packed atomic planes. However, the stacking sequence is different. The second lattice plane is initially stacked as in the hcp-lattice and sits in the gaps of the underlying layer. In contrast to the hcp-structure, however, the third atomic layer is located in the “free” gaps. Accordingly, the stacking sequence of the closest packed planes results in the series ABCABC …
Typical metals with a face-centered cubic lattice structure are aluminum, lead, copper and nickel. As in the hcp-lattice, an atom in the fcc-lattice has 12 neighboring atoms. The coordination number is therefore also 12.
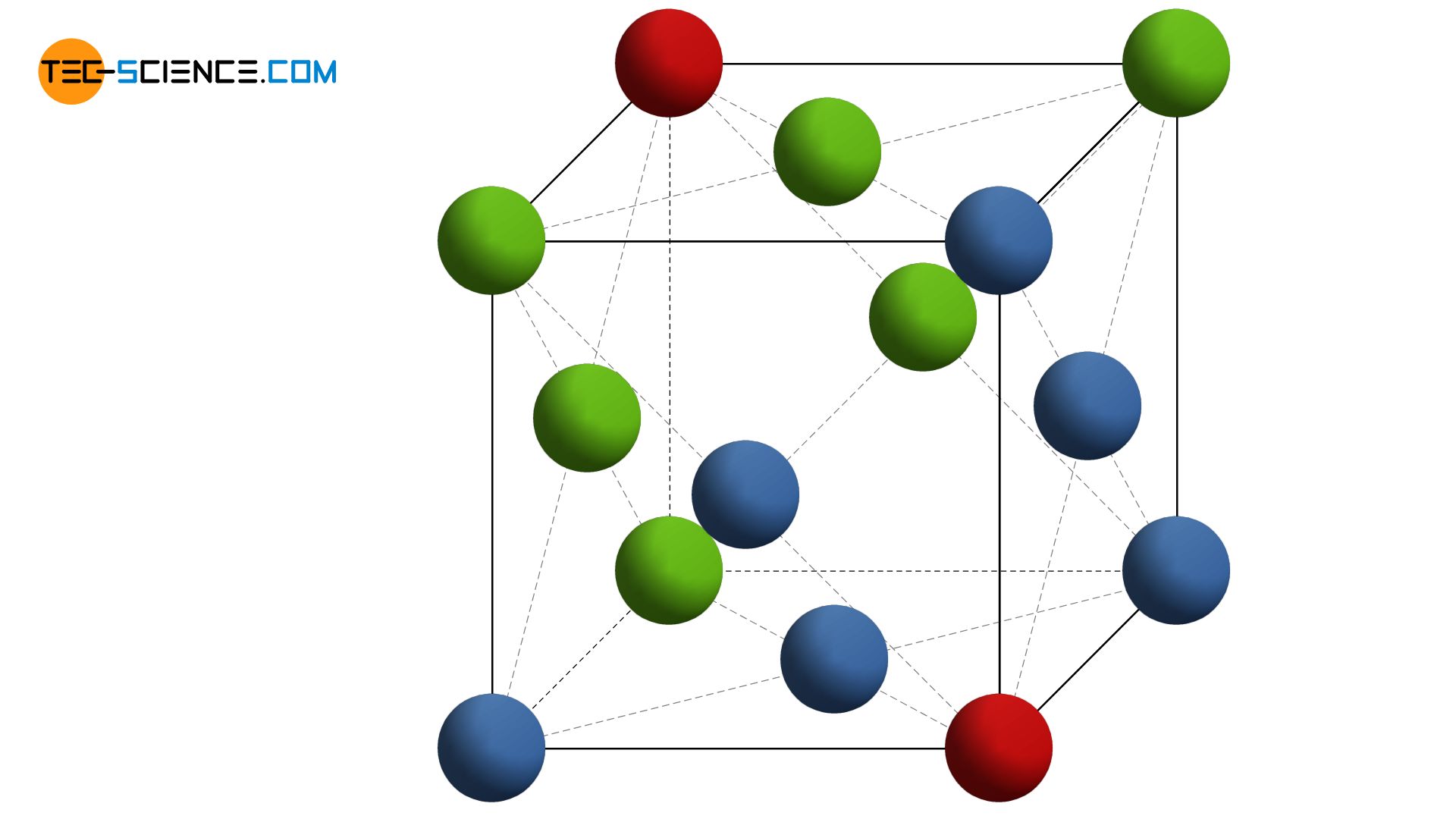
In a face-centered cubic lattice, the basic shape of the unit cell is not hexagonal, as might be suggested by its similar structure to the hexagonal lattice. The unit cell actually has the shape of a cube and is therefore one of the cubic crystal systems! Regarding the horizontally aligned closest packed planes, the unit cell stands on the corner of the cube. The anomation above shows that besides the atoms in the corner of the cube, other atoms are centered on the cube surfaces. Therefore, this type of lattice is called face-centered.
In the face-centered cubic lattice (fcc), there is another atom next to the corner atoms on the surfaces of the cubic unit cell!
Note that the fcc and hcp lattice differ only in the stacking sequence of the closest packed planes (ABCABC … or ABAB …)! The packing density in the face-centered cubic lattice is therefore identical to the maximum possible packing density of 74 %.
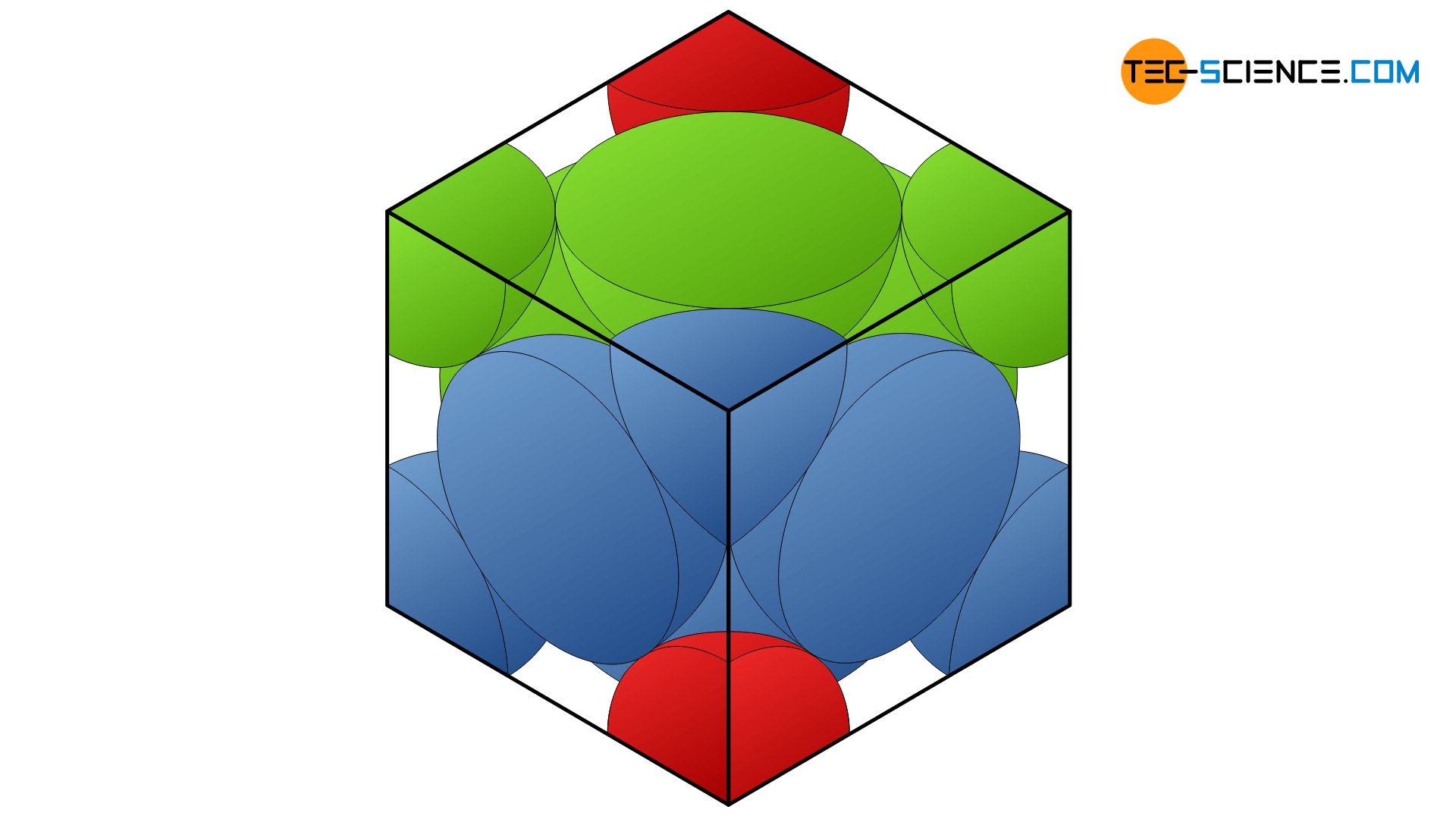
However, the seemingly small difference in the stacking sequence between the fcc-lattice and the hcp-lattice has enormous effects on the mechanical properties, especially on the ductility of these structures. The reason for this will be explained in more detail in the ductility.