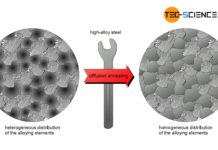
The aim of stress-relief annealing is to release residual stresses!
If a steel is heated or cooled unevenly, internal stresses can arise, also known as residual stresses. Such residual stresses are often induced during welding, for example, because the workpiece is heated not evenly but only locally at a certain point and then cooled down. However, residual stresses can also occur in the workpiece during milling or turning, as high temperatures can occur in the machining area of the workpiece. During hardening, the quench distortion is also based on the residual stresses caused by the uneven cooling.
Such residual stresses can, among other things, reduce the strength of the workpiece. Furthermore, residual stresses during a subsequent machining process can also lead to distortion of the workpiece if the residual stresses are suddenly released as a result. Therefore, in some cases it is necessary to eliminate residual stresses in the workpiece. This is achieved by stress relief annealing.
The aim of stress-relief annealing is to release residual stresses!
In stress relief annealing, the workpiece is annealed below the PSK-line in the range between 550 °C and 650 °C. The effect of the stress relief is based on the fact that the strength of the heated material decreases at a higher temperature. If the yield strength (hot yield strength) falls below the value of the residual stresses, these are reduced by plastic deformation. The dislocations begin to move accordingly.
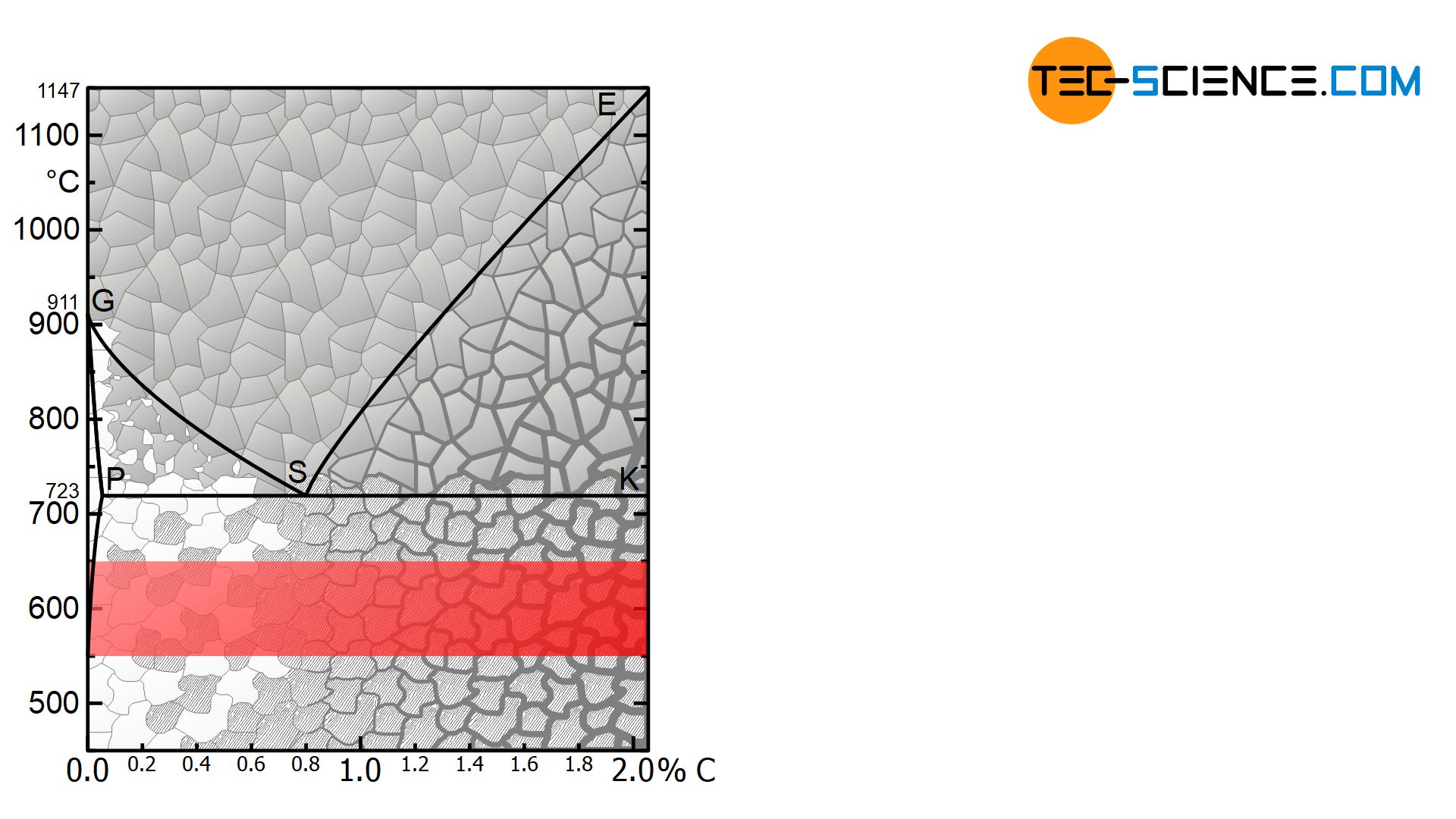
The residual stresses can therefore only ever be reduced to a maximum of the corresponding hot yield point, never completely. After annealing, the workpiece must then be cooled slowly to avoid a renewed occurrence of stress. In most cases, the workpiece remains stationary in the switched-off annealing furnace.