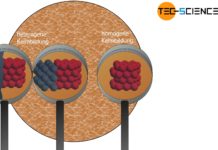
Bei der heterogenen Keimbildung lösen Keime, die nicht aus der gleichen Substanz wie die Schmelze bestehen, die Erstarrung aus.
Einleitung
Die im Abschnitt homogene Keimbildung betrachtete Keimbildung bezog sich auf die eigenen Teilchen in der Schmelze (Eigenkeime). Die größte Hemmschwelle bei dieser homogenen Keimbildung ist das Aufbringen der Oberflächenenergie. Dies führt dazu, dass kleine Keime nicht wachstumsfähig sind und sich dementsprechend auflösen.
Eine Verringerung der Oberflächenenergie bedeutet deshalb, dass eine geringere Aktivierungsenergie für die Keimbildung erforderlich. Somit sind bereits kleinere Keime stabil und lösen sich nicht sofort wieder auf. Die thermischen Schwankungen wären dann vermehrt in der Lage wachstumsfähige Keime zu bilden.
An dieser Stelle können Verunreinigungen, Fremdteilchen oder die Gefäßwände sehr hilfreich sein (allgemein auch als Substrat bezeichnet), da genau diese einen Teil der notwendigen Oberflächenenergie für die Keimbildung aufbringen. Man spricht dann von heterogener Keimbildung, die weniger Aktivierungsarbeit (Keimbildungsarbeit) als die homogene Keimbildung erfordert.
Fremdteilchen können einen Teil der Keimbildungsarbeit aufbringen, sodass bereits kleinere Keime wachstumsfähig sind!
Da eine Schmelze in der Regel stets solche Fremdkörper beinhaltet, ist die heterogene Keimbildung deshalb wesentlich wahrscheinlicher als die homogene Keimbildung.
Benetzung
Die Herleitung der Gesetzmäßigkeiten für die heterogene Keimbildung erfolgt auf analogem Wege wie für die homogene Keimbildung. Exemplarisch soll im Folgenden eine glatte Gefäßwand (Kokille) zur Schmelze hin dienen an der sich ein Keim bildet. Aufgrund der wirkenden Oberflächenspannungen hat der erstarrte Keim dabei die Form einer abgeschnittenen Kugel.
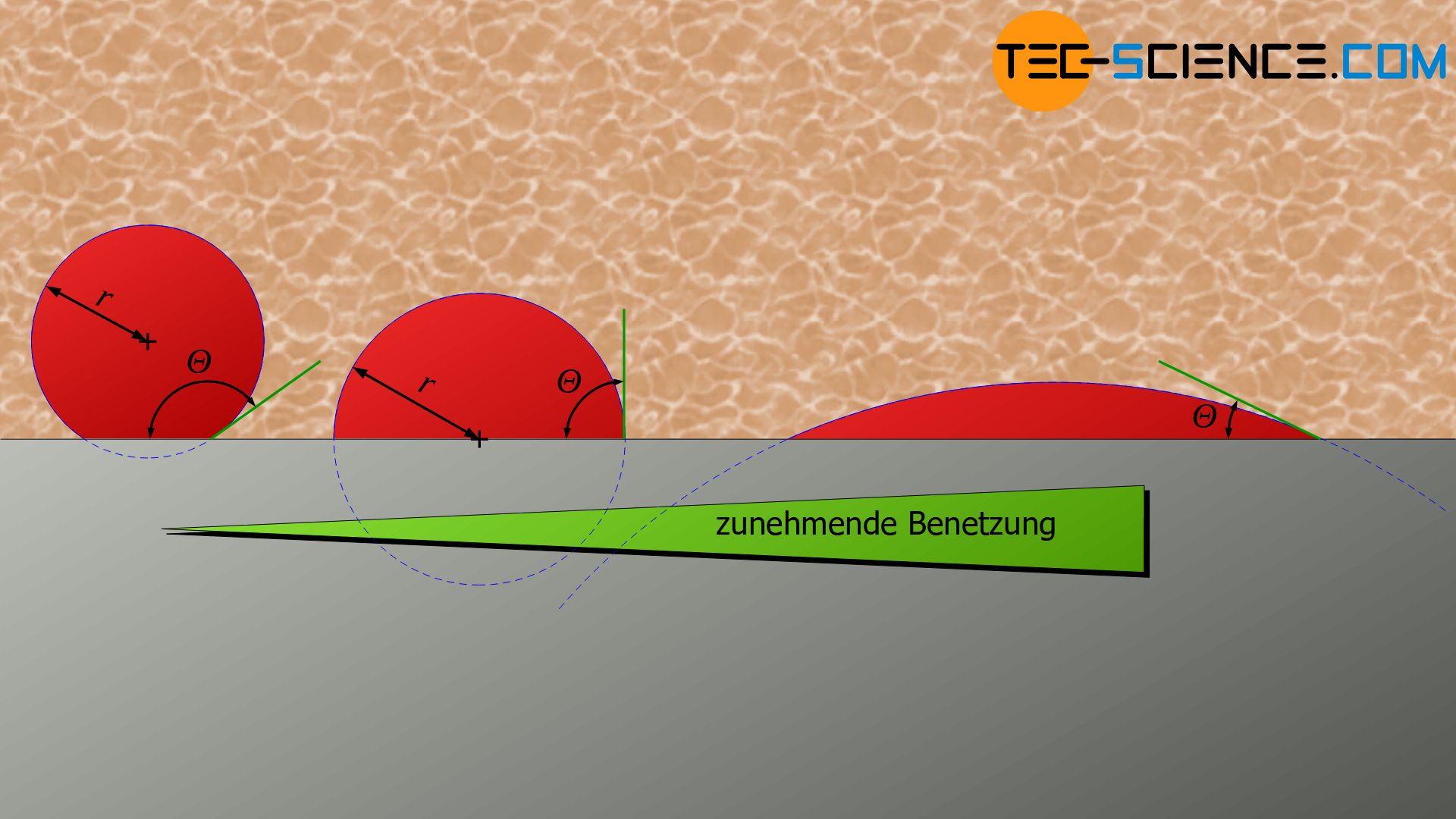
Der Winkel am Kontaktpunkt zwischen Keimoberfläche und Gefäßwand wird auch als Benetzungswinkel \(\Theta\) oder Kontaktwinkel bezeichnet. Je nach Wechselwirkung zwischen Keim, Schmelze und Wand wird die Wand sehr stark vom Keim benetzt (geringer Benetzungswinkel) oder kaum benetzt (großer Benetzungswinkel). Dies hat dementsprechend Auswirkungen auf die Form des kugelsegmentförmigen Keims.

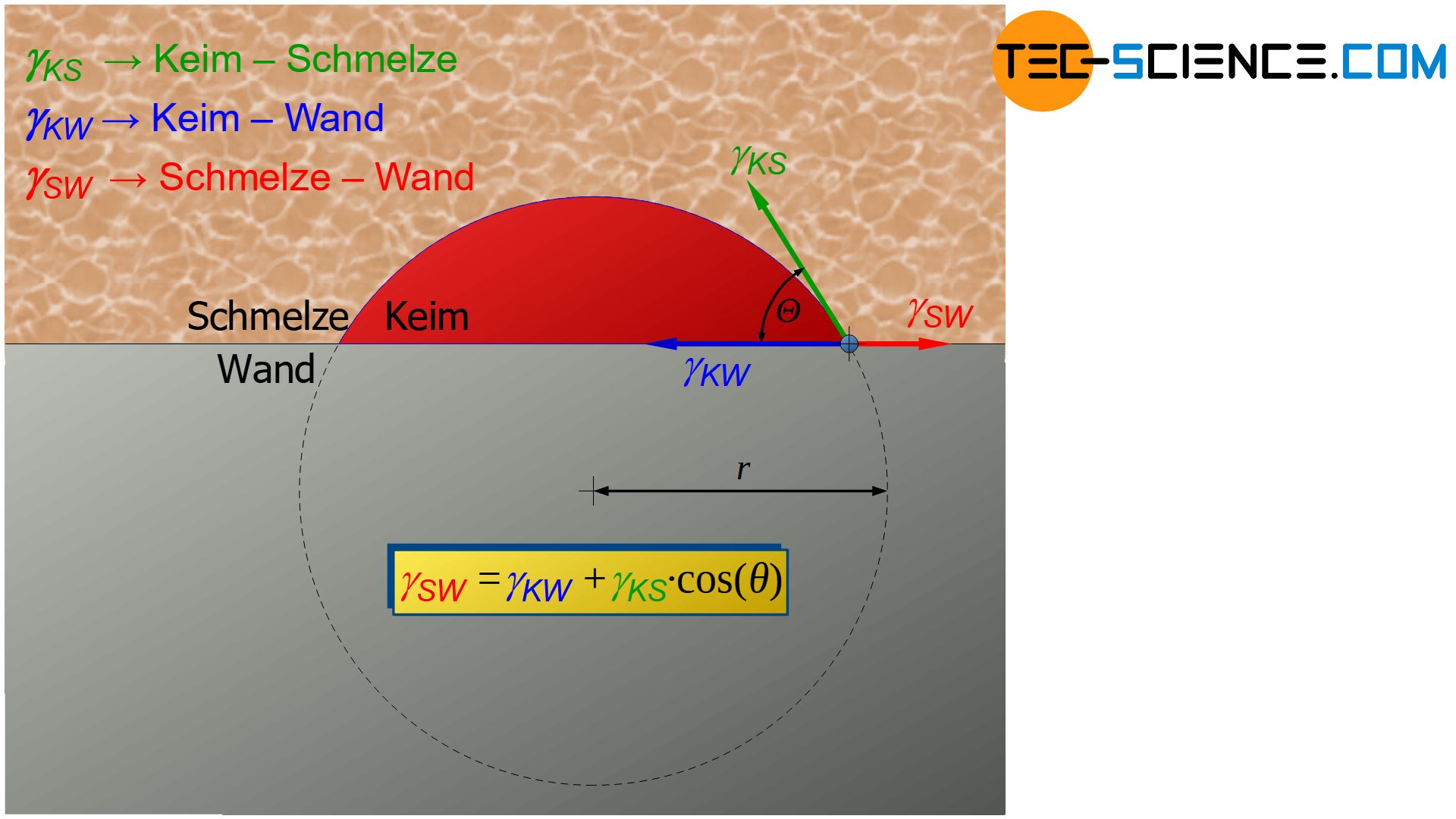
Entscheidend für den Kontaktwinkel \(\Theta\) sind die spezifischen Oberflächenenergien bzw. Oberflächenspannungen \(\gamma\) zwischen den besagten Grenzflächen Keim-Schmelze (\(\gamma_{KS}\)), Keim-Wand (\(\gamma_{KW}\)) und Schmelze-Wand (\(\gamma_{SW}\)). Aus einer Gleichgewichtsbetrachtung ergibt sich dabei folgende Beziehung (Young-Gleichung):
\begin{align}
\label{benetzungswinkel}
\boxed{\cos\Theta = \frac{\gamma_{SW}-\gamma_{KW}}{\gamma_{KS}}} ~~~\text{Young-Gleichung} \\[5px]
\end{align}
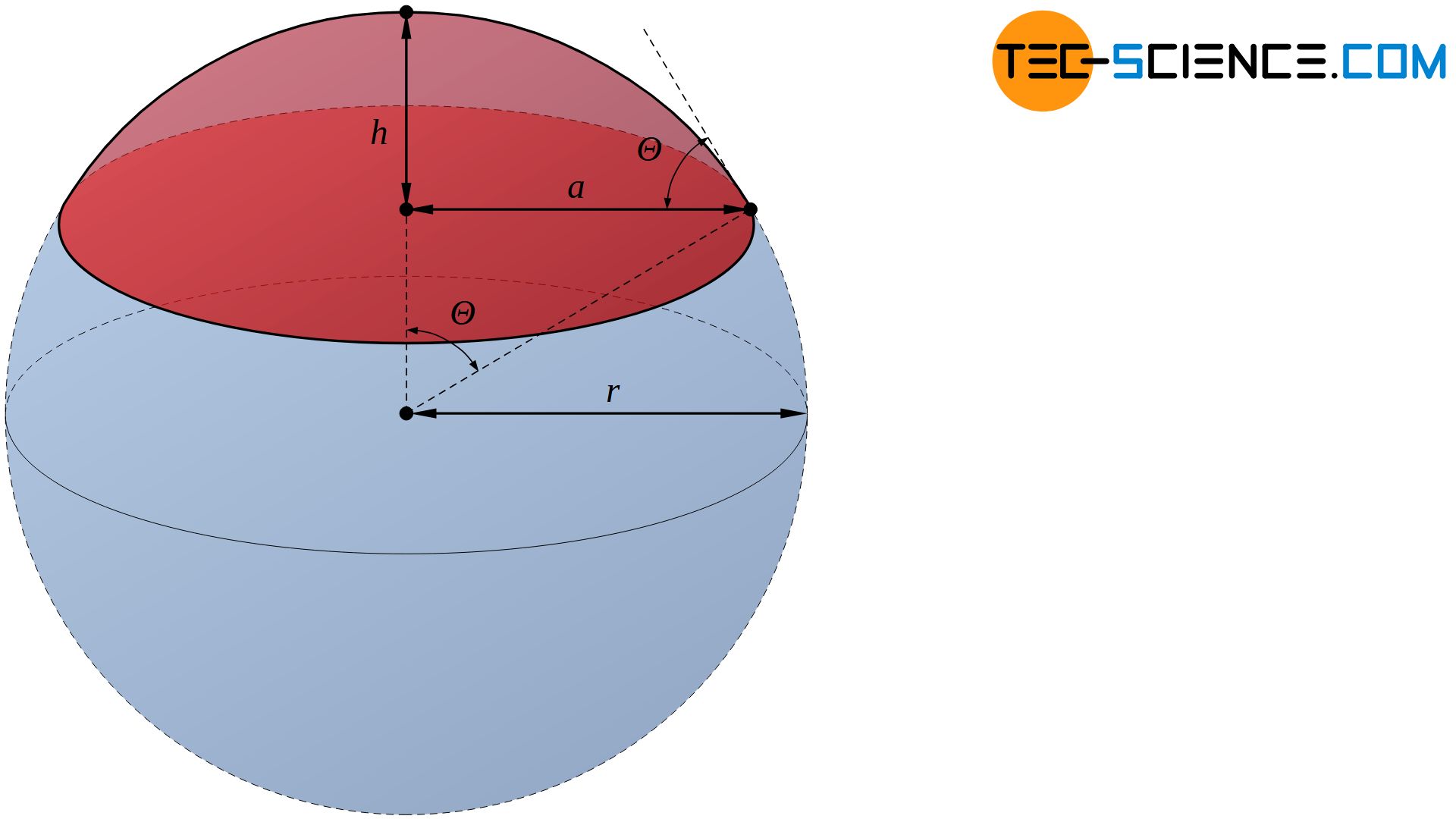
Anhand des Benetzungswinkels \(\Theta\) kann schließlich auch das Volumen \(V\) des Kugelsegmentes bei gegebenem Keimradius \(r\) durch nachfolgend angegeben Gleichung ermittelt werden:
\begin{align}
&V= \tfrac{1}{3} h^2 \pi \left(3r – h \right) ~~~\text{mit}~~~ h=r\left(1-\cos\Theta \right) ~~~\text{folgt:} \\[5px]
\label{kuppelvolumen}
&\boxed{V= \tfrac{1}{3} \pi \left(2-3\cos\Theta+\cos^3\Theta \right)r^3} \\[5px]
\end{align}
Ebenfalls lässt sich über den Benetzungswinkel \(\Theta\) die Oberfläche der Kugelkappe \(O_S\) ermitteln, die die Grenzfläche zwischen Keim und Schmelze bildet.
\begin{align}
&O_S= 2\pi r h ~~~\text{mit}~~~ h=r\left(1-\cos\Theta \right) ~~~\text{folgt:} \\[5px]
\label{mantelflaeche}
&\boxed{O_S= 2 \pi \left(1-\cos\Theta \right) r^2} \\[5px]
\end{align}
Die sich zur Wand bildende Basisfläche \(O_W\) des Kugelsegmentes ist ebenfalls vom Benetzungswinkel \(\Theta\) abhängig:
\begin{align}
&O_W= \pi a^2 ~~~\text{mit}~~~ a=r~\sin\Theta ~~~\text{folgt:} \\[5px]
\label{basisflaeche}
&\boxed{O_W= \pi \sin^2\Theta \cdot r^2} \\[5px]
\end{align}
Gibbs Energie eines Keims
Im Falle der heterogenen Keimbildung setzt sich die Änderung der Gibbs-Energie \(\Delta G_{Keim}\) eines sich bildenden Keims aus drei Teilen zusammen:
\begin{align}
\label{0}
\boxed{\Delta G_{Keim} = \Delta G_{V} + \Delta G_{O,KS} + \Delta G_{O,KW}}
\end{align}
- Verringerung der Volumenenergie \(\Delta G_V\) aufgrund der Phasenänderung
- Aufzubringende Oberflächenenergie \(\Delta G_{O,KS}\) an der Grenzfläche zwischen Keim und Schmelze
- Änderung der Oberflächenenergie \(\Delta G_{O,KW}\) während der Phasenänderung zwischen Keim und Wand
Auf diese Terme wird im folgenden näher eingegangen.
Verringerung der Volumenenergie aufgrund der Phasenänderung
Die Änderung der „Volumenenergie“ \(\Delta G_V\) ist durch das Volumen \(V\) des Keims in Kombination mit der Dichte \(\rho\) und der spezifischen Gibbs-Energieänderung \(\Delta g_{V}\) gegeben (Beachte, dass dieser Teil zur Erniedrigung der Energie führt und deshalb im Gegensatz zur aufzubringenden Oberflächenenergie ein negatives Vorzeichen trägt):
\begin{align}
&\Delta G_{V} = – m \cdot \Delta g_V ~~~~~\text{mit}~~~~m = V \cdot \rho ~~~~ \text{folgt:} \\[5px]
\label{321}
&\underline{\Delta G_{V} = – V \cdot \rho \cdot \Delta g_V } \\[5px]
\end{align}
Die spezifische Änderung der Gibbs-Energie \(\Delta g_{V}\) kann durch die Beziehung zur spezifischen Schmelzwärme \(q_E\), Erstarrungstemperatur \(T_E\) und zur Unterkühlung \(\Delta T\) ausgedrückt werden (Herleitung siehe hier):
\begin{align}
\label{schmelz}
&\underline{\Delta g_V = q_E \cdot \frac{\Delta T}{T_E}} \\[5px]
\end{align}
Werden die Gleichungen (\ref{kuppelvolumen}) und (\ref{schmelz}) in Gleichung (\ref{321}) eingesetzt, dann ergibt sich die aufzuwendende Volumenenergie \(\Delta G_V\) aufgrund der Phasenänderung des Keims wie folgt:
\begin{align}
\label{2}
&\boxed{\Delta G_{V} = – \frac{\pi~\rho~q_E}{3~T_E} \Delta T \left(2-3\cos\Theta+\cos^3\Theta \right) \cdot r^3} \\[5px]
\end{align}
Aufzubringende Oberflächenenergie an der Grenzfläche zwischen Keim und Schmelze
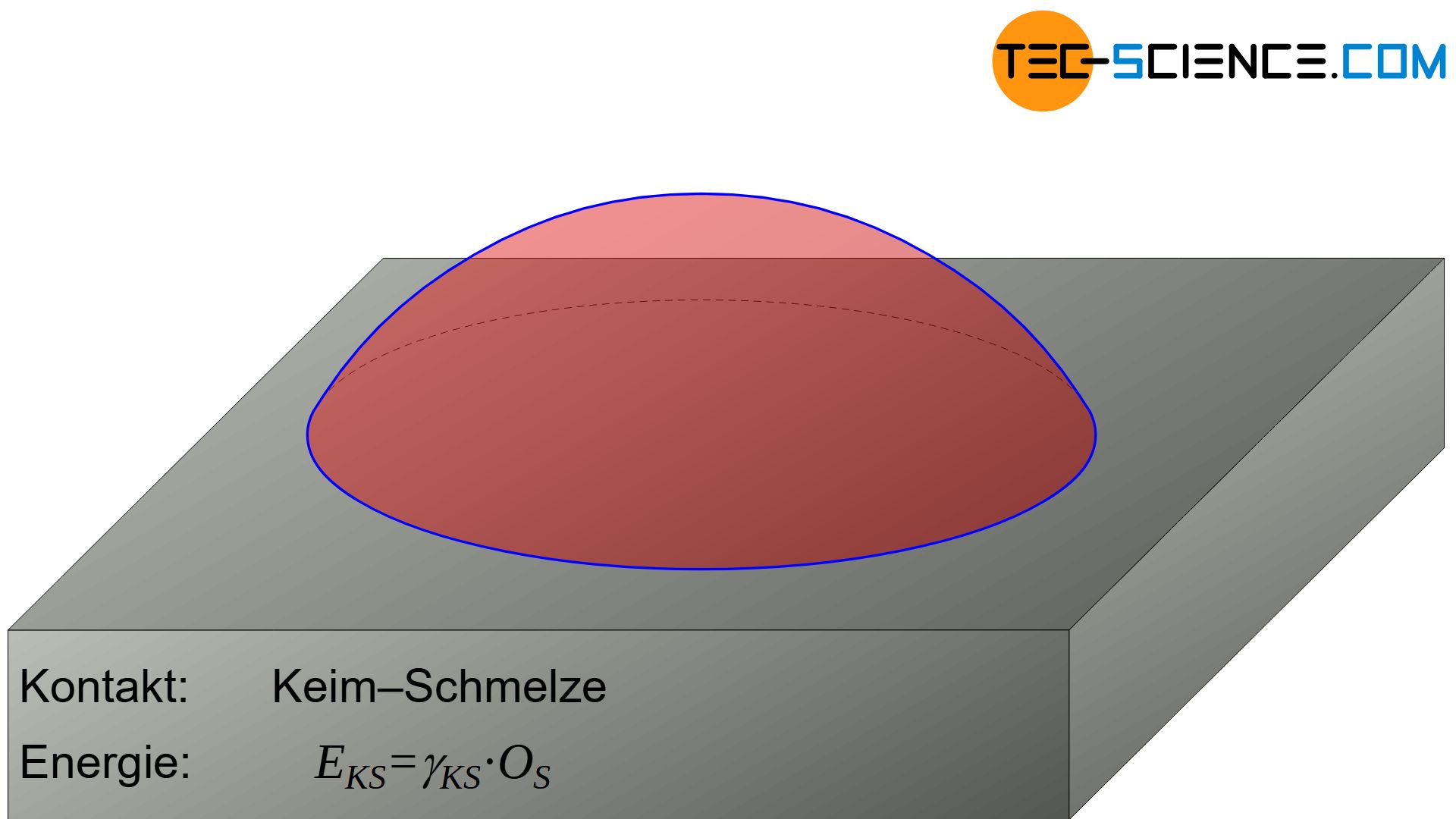
Die aufzuwendende Oberflächenenergie \(\Delta G_{O,KS}\) zur Erzeugung der Keimoberfläche zur Schmelze hin ergibt sich über die Kugelkappe \(O_S\) und die entsprechende spezifische Oberflächenenergie \(\gamma_{KS}\):
\begin{align}
&\underline{\Delta G_{O,KS} = \gamma_{KS} \cdot O_S} \\[5px]
\end{align}
Mit Hilfe von Gleichung (\ref{mantelflaeche}) ist die aufzuwendende Oberflächenenergie \(\Delta G_{O,KS}\) zur Erzeugung der Keimoberfläche zur Schmelze hin wie folgt gegeben:
\begin{align}
\label{3}
&\boxed{\Delta G_{O,KS} = 2 \pi~\gamma_{KS}~\left(1-\cos\Theta \right) r^2} \\[5px]
\end{align}
Änderung der Oberflächenenergie an der Kontaktfläche zur Wand
Im schmelzflüssgen Zustand ergibt sich die Oberflächenenergie \(E_{SW}\) an der Kontaktfläche zwischen dem noch nicht gebildeten Keim (= Schmelze) und der Wand wie folgt:
\begin{align}
E_{SW}=\gamma_{SW} \cdot O_W \\[5px]
\end{align}
Durch die Bildung des Keims ändert sich nun die Oberflächenenergie zwischen ehemals Schmelze/Wand hin zu Keim/Wand mit der entsprechenden Oberflächeenergie \(E_{KW}\):
\begin{align}
E_{KW}=\gamma_{KW} \cdot O_W \\[5px]
\end{align}
Folglich hat sich durch den erstarrten Keim die Oberflächenenergie an der Kontaktstelle zur Wand – und mit ihr die Gibbs’sche Energie des Keims – wie folgt geändert:
\begin{align}
\label{d}
&\underline{\Delta G_{O,KW} = (\gamma_{KW}-\gamma_{SW}) \cdot O_W} \\[5px]
\end{align}
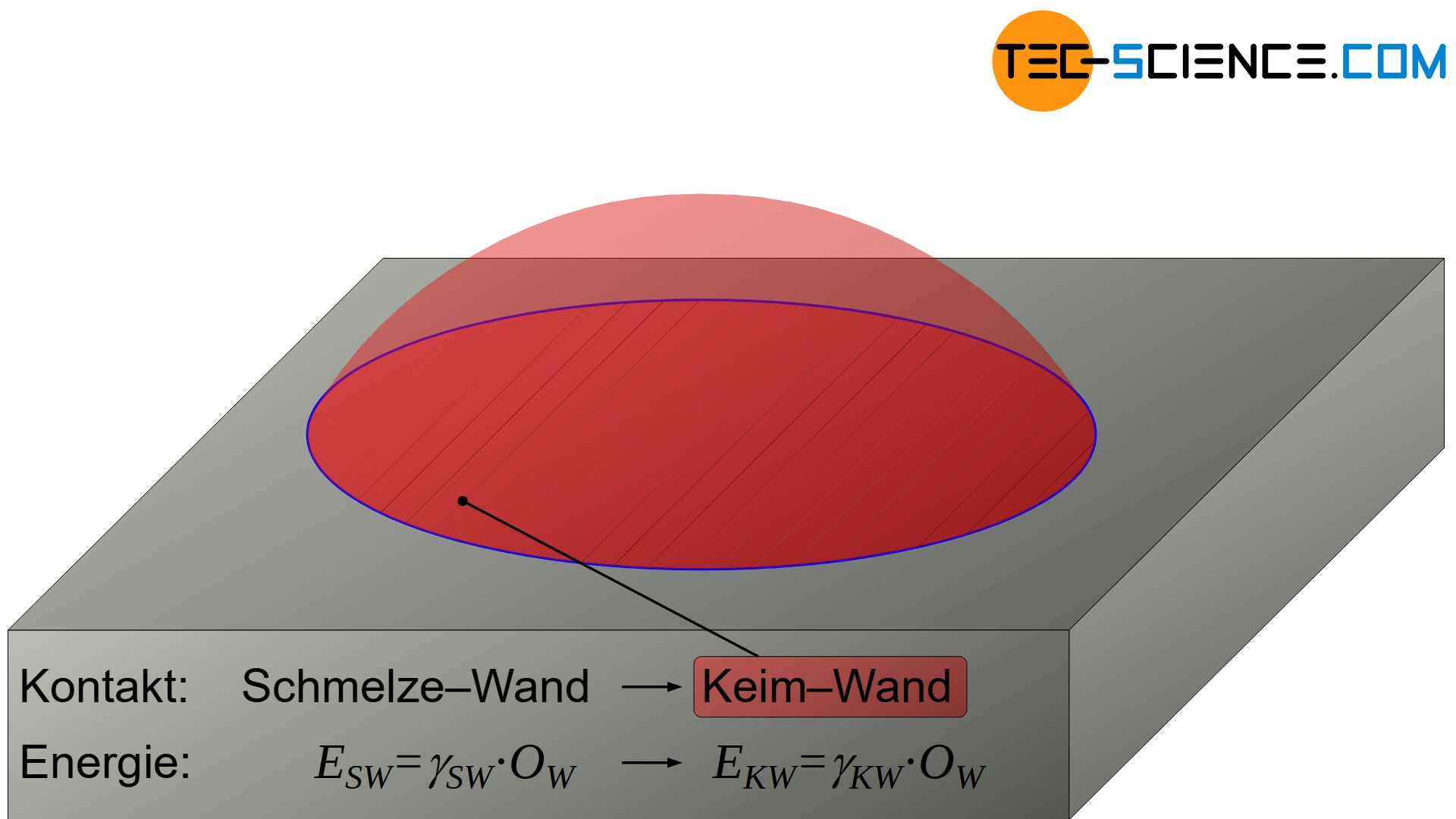
Bereits an dieser Stelle zeigt sich der energetische Vorteil der heterogenen Keimbildung. Die Oberflächenenergie des Keims zur Wand hin muss nicht von Null an aufgebracht sondern nur geändert werden (\(\gamma_{SW}>0\))!
Während die Kontaktoberfläche \(O_W\) nach Gleichung (\ref{basisflaeche}) bestimmt ist, kann die Differenz der Oberflächenspannungen durch Gleichung (\ref{benetzungswinkel}) ersetzt werden:
\begin{align}
\label{young}
&\underline{\gamma_{KW}-\gamma_{SW} = -\gamma_{KS}\cdot \cos(\Theta)} \\[5px]
\end{align}
Werden die Gleichungen (\ref{basisflaeche}) und (\ref{young}) in die Gleichung (\ref{d}) eingesetzt, dann kann die Änderung der Oberflächenenergie an der Kontaktstelle zur Wand \(\Delta G_{O,KW}\) wie folgt ermittelt werden:
\begin{align}
\underline{\Delta G_{O,KW} = -\gamma_{KS} \cdot \cos\Theta \cdot \pi \sin^2\Theta \cdot r^2} \\[5px]
\end{align}
Ferner kann ausgenutzt werden, dass der geometrische Ausdruck \( \cos(\Theta) \cdot \sin^2(\Theta) \) durch den Term \( \cos(\Theta) – \cos^3(\Theta) \) ersetzt werden kann. Damit gilt schließlich:
\begin{align}
\label{1}
&\boxed{\Delta G_{O,KW} = -\pi~\gamma_{KS}~ \left(\cos\Theta – \cos^3\Theta \right) \cdot r^2} \\[5px]
\end{align}
Gesamtänderung der Gibbs-Energie des Keims
Die Änderung der Gibbs-Energie \(\Delta G_{Keim}\) des erstarrenden Keims kann durch Einsetzen der Gleichungen (\ref{2}), (\ref{3}) und (\ref{1}) in Gleichung (\ref{0}) und anschließendes Zusammenfassen somit wie folgt ausgedrückt werden:
\begin{align}
\Delta G_{Keim} = &- \frac{\pi~\rho~q_E}{3~T_E} ~\Delta T \left(2-3\cos\Theta+\cos^3\Theta \right) \cdot r^3 \\[5px]
&+ 2 \pi~\gamma_{KS}~\left(1-\cos\Theta \right) r^2 \\[5px]
&- \pi~\gamma_{KS}~ \left(\cos\Theta – \cos^3\Theta \right) \cdot r^2 \\[5px]
\Delta G_{Keim} = &- \frac{\pi~\rho~q_E}{3~T_E} ~\Delta T \left(2-3\cos\Theta+\cos^3\Theta \right) \cdot r^3 \\[5px]
&+ \pi~\gamma_{KS}~\left( 2-3\cos\Theta+\cos^3\Theta \right) ~r^2 \\[5px]
\end{align}
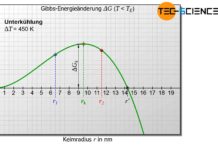
Durch weitere Zusammenfassungen kann die Änderung der Gibbs-Energie eines als kugelförmig angenommenen (benetzenden) Keims mit dem Radius \(r\) bei der gegebenen Unterkühlung \(\Delta T\) wie folgt dargestellt werden:
\begin{align}
\label{heterogene}
\boxed{\Delta G_{Keim}(\Delta T, r) =\tfrac{1}{4}\left(2-3\cos\Theta+\cos^3\Theta \right) ~ \left[-\frac{4~\pi~\rho~q_E}{3~T_E}~\Delta T~r^3 + 4\pi~\gamma_{KS}~r^2 \right]} \\[5px]
\end{align}
Diese Gleichung wird im folgenden Abschnitt näher diskutiert.
Vergleich der heterogenen mit der homogenen Keimbildung
Interessant ist an dieser Stelle ein Vergleich mit der Energieänderung eines vergleichbaren Keims bei der homogenen Keimbildung:
\begin{align}
\label{keim}
&\boxed{\Delta G_{hom}(\Delta T, r) = -\frac{4 \pi \rho ~ q_E}{3 ~ T_E} \cdot \Delta T \cdot r^3 + 4 \pi ~ \gamma \cdot r^2} \\[5px]
\end{align}
Bei gleichem Radius und gleicher Unterkühlung unterscheidet sich die Energieänderung bei heterogener Keimbildung um den geometrischen Faktor der sich vor dem Term in den eckigen Klammern der Gleichung (\ref{heterogene}) befindet (Benetzungsfaktor).
Der Term in den eckigen Klammern selbst entspricht gerade der Energieänderung bei der homogenen Keimbildung. Energetisch betrachtet ist somit die heterogene Keimbildung an einer glatten Wand wie folgt mit der homogenen Keimbildung verknüpft:
\begin{align}
\boxed{\Delta G_{het} =f(\Theta) \cdot \Delta G_{hom}} ~~~ \text{mit} ~~~ \boxed{f(\Theta)=\tfrac{1}{4}\left(2-3\cos\Theta+\cos^3\Theta \right)} \le 1 \\[5px]
\end{align}
Der kritische Keimradius ist bei der heterogenen Keimbildung grundsätzlich derselbe wie bei der homogenen Keimbildung, lediglich die Aktivierungsenergien unterscheiden sich (bei ansonsten gleichen Bedingungen). Beachte, dass es sich bei der heterogenen Keimbildung zwar um denselben (fiktiven) Keimradius handelt, aber letztlich nur ein Teil des Kugelvolumens tatsächlich den eigentlich Keim bildet.
Der kritische Keimradius kann prinzipiell auf dieselbe Weise wie bei der homogenen Keimbildung durch Ableiten und Nullsetzen von Gleichung (\ref{heterogene}) erhalten werden:
\begin{align}
&\frac{d (\Delta G_{\text{Keim}})}{dr} = 0 \\[5px]
& \tfrac{1}{4}\left(2-3\cos\Theta+\cos^3\Theta \right) \cdot \left[-\frac{4 \pi \rho ~ q_E}{T_E} \cdot \Delta T \cdot r^2 + 8 \pi \gamma_{KS} \cdot r \right] = 0 \\[5px]
& \frac{4 \pi \rho ~ q_E}{T_E} \cdot \Delta T \cdot r = 8 \pi \gamma_{KS} \\[5px]
& \boxed{r_{k,het} = \frac{2 \gamma_{KS} ~ T_E}{q_E~ \rho ~\Delta T}}=r_{k,hom}
\end{align}
Einsetzen des kritischen Keimradius \(r_{k,het}\) in Gleichung (\ref{heterogene}) liefert die Aktivierungsenergie der heterogenen Keimbildung \(\Delta G_{k,het}\), mit dem bereits erläuterten Zusammenhang zur homogenen Keimbildung:
\begin{align}
&\boxed{\Delta G_{k,het} = \tfrac{1}{4}\left(2-3\cos\Theta+\cos^3\Theta \right) \cdot \left[\frac{16 ~\pi ~ \gamma_{KS}^3 ~ T_E^2}{3 ~ q_E^2 ~ \rho^2 ~ \Delta T^2}\right] } \\[5px]
\end{align}
bzw.
\begin{align}
&\boxed{\Delta G_{k,het} = f(\Theta) \cdot \Delta G_{k,hom}} ~~~ \text{mit} ~~~ \boxed{f(\Theta)=\tfrac{1}{4}\left(2-3\cos\Theta+\cos^3\Theta \right)} \le 1 \\[5px]
\end{align}
Der rein vom Benetzungswinkel abhängige Term ist dabei stets kleiner 1, sodass an dieser Stelle ersichtlich wird, dass die heterogene Keimbildung eine geringere Aktivierungsenergie benötigt als die homogene Keimbildung.
Für einen Benetzungswinkel von \(\Theta\)=90° ist der Keim eine Halbkugel und der Benetzungsfaktor besitzt den Wert \(f(\Theta)\)=0,5. Der Keim benötigt in diesem Fall nur die Hälfte der Aktivierungsenergie, schließlich besitzt er auch nur ein halb so großes Volumen im Vergleich zu einem kugelförmigen Keim bei der homogenen Keimbildung.
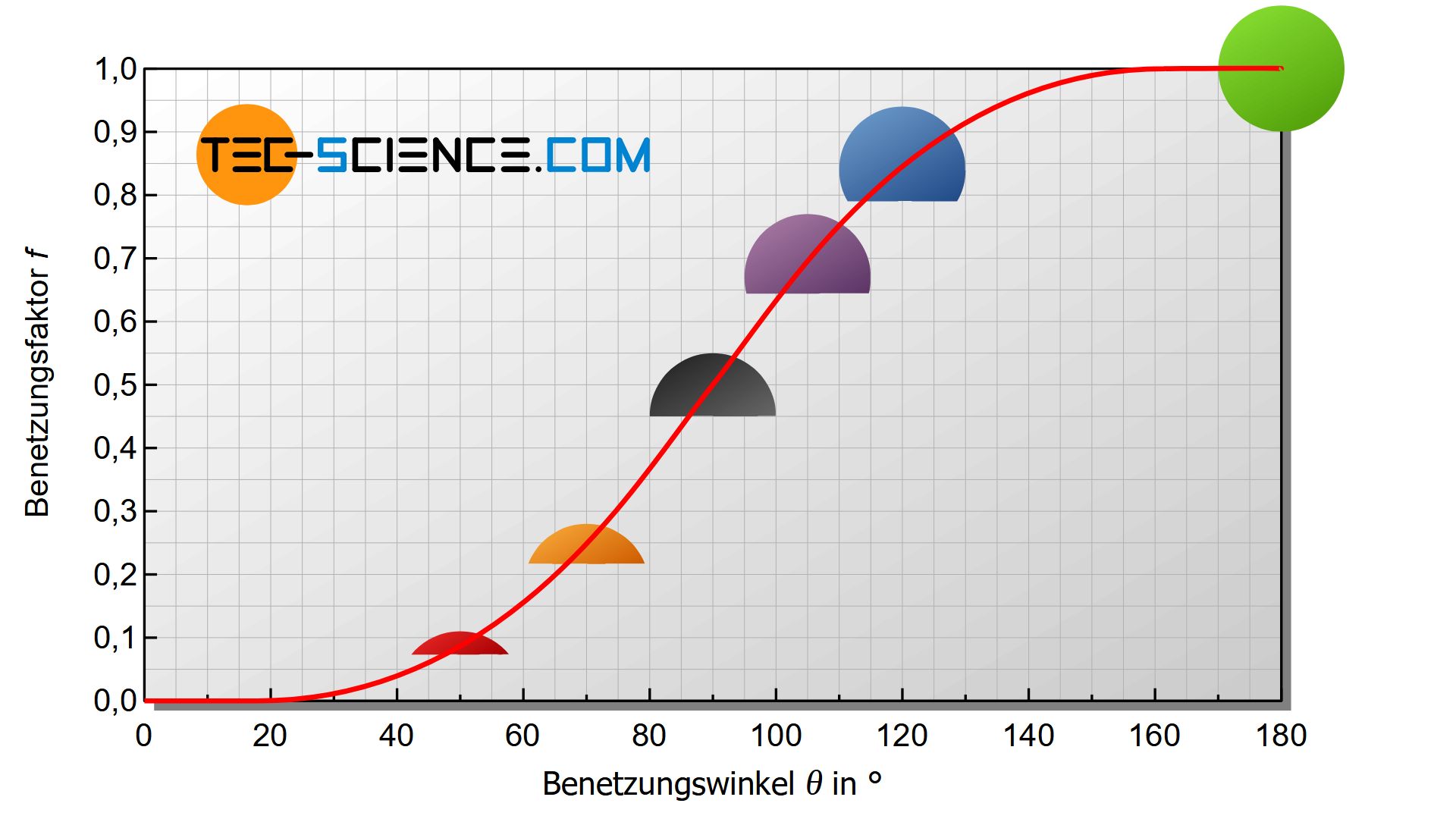
Bei größeren Benetzungswinkeln steigt der Benetzungsfaktor mehr und mehr an. Bei einem Winkel von \(\Theta\)=180° erreicht dieser Benetzungsfaktor schließlich sein Maximum von 1. Der Kugelabschnitt ist zu einer runden Kugel geworden, die die Wand nicht mehr benetzt. Man erhält als Spezialfall dann die homogene Keimbildung!
Umgekehrt erhält man für kleine Benetzungswinkel, d.h. für sehr starke Benetzungen, sehr kleine Benetzungsfaktoren. Die zur Keimbildung notwendige Aktivierungsenergie sinkt folglich sehr stark. Mit geringerem Benetzungswinkel nimmt bei gleichem kritischen Radius das Keimvolumen dann ebenfalls sehr stark ab. Es müssen für die Keimbildung dann nicht mehr so viele Atome zur Verfügung gestellt werden.
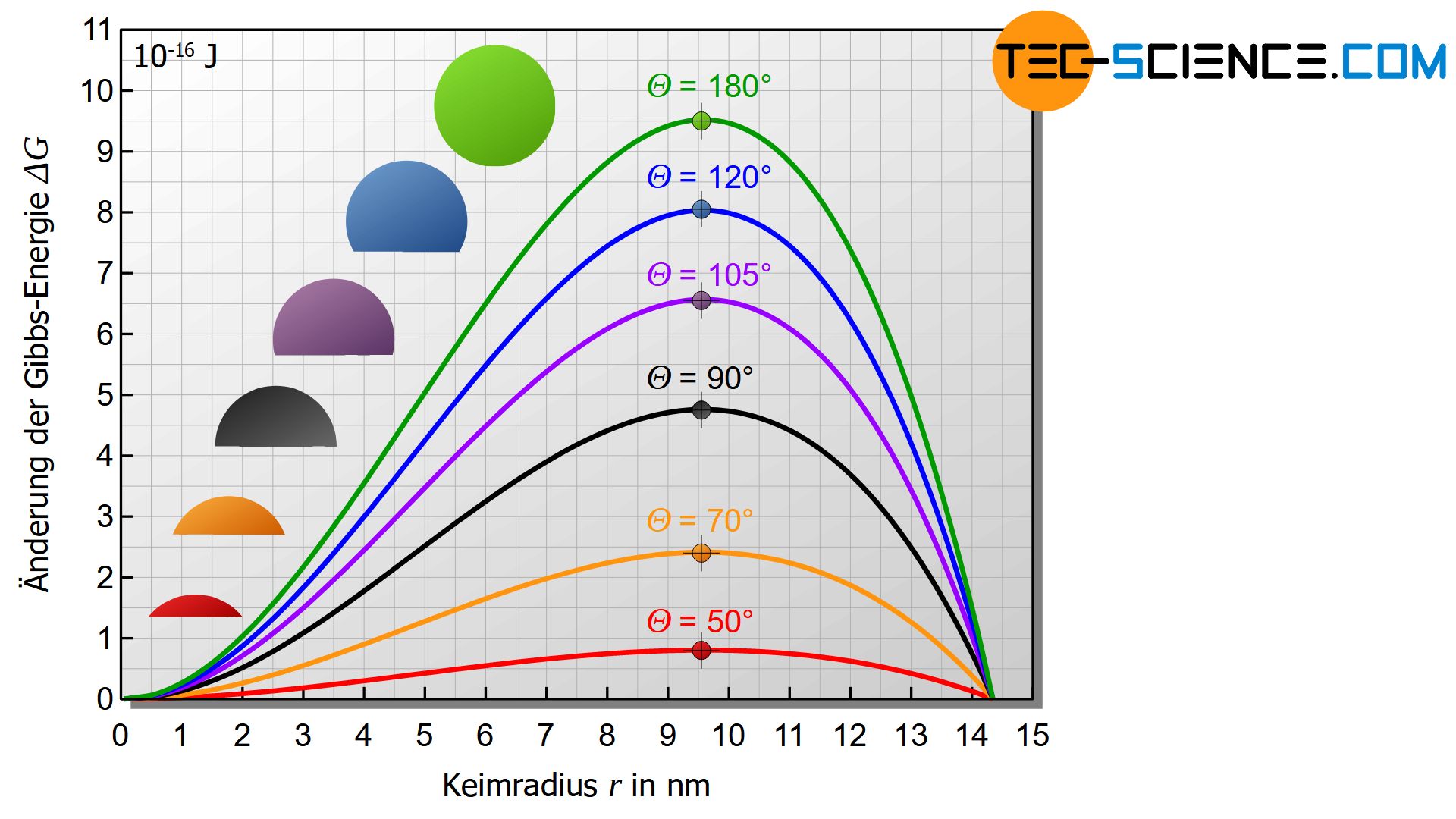
Bei einem Benetzungswinkel von \(\Theta\)=20° sinkt bspw. die benötigte Anzahl an Atomen im Vergleich zum bereits vorgestellten Beispiel bei der homogenen Keimbildung von 300.000 Atome auf nunmehr nur 800 Atome (bei ansonsten gleichen Bedingungen).
Um denselben Faktor nimmt die Aktivierungsenergie von ursprünglich 9,5·10-16 J auf 0,025·10-16 J ab. Somit wird auch auf anschaulichem Wege nochmals deutlich, dass die heterogene Keimbildung sehr viel wahrscheinlicher ist als die homogene.
Die heterogene Keimbildung funktioniert dann besonders gut, wenn sich die eingebrachte Fremdkörper (Impfteilchen) bzw. die Gefäßwände sehr gut benetzen lassen.
Beim Einbringen von Impfkristallen in die Schmelze ist darauf zu achten, dass die Impfteilchen einen größeren Radius aufweisen als der des kritischen Radius der Keimbildung. Gleichzeitig besteht jedoch die Gefahr, dass sich die Teilchen in der heißen Schmelze auflösen bevor die Keimbildung hätte beginnen können. Deshalb werden die Impfteilchen häufig unmittelbar beim Abgießen in die unterkühlte Schmelze eingebracht.