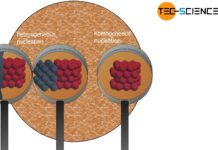
In heterogeneous nucleation, nuclei that do not consist of the same substance as the melt trigger solidification.
Introduction
The nucleation considered in the article homogeneous nucleation referred to the own particles in the melt. The greatest threshold for the homogeneous nucleation to take place is the surface energy that needs to be applied. This results in small nuclei not being able to grow and therefore dissolving again.
A reduction in surface energy therefore means that less activation energy (free energy barrier) is required for nucleation. Thus even small nuclei are stable and do not dissolve immediately. The thermal fluctuations would then be able to form more growth-capable nuclei.
At this point, impurities, foreign particles or the vessel walls can be very helpful (generally referred to as substrate), as they apply part of the surface energy required for nucleation. This is called heterogeneous nucleation, which requires less activation energy than homogeneous nucleation.
Foreign particles can apply part of the activation energy, so that even smaller nuclei can grow!
Since a melt usually always contains such foreign particles, heterogeneous nucleation is therefore much more likely than homogeneous nucleation.
Wetting
The laws for heterogeneous nucleation are derived in the same way as for homogeneous nucleation. The following example shows a smooth vessel wall (mold) towards the melt on which a nucleus forms. Due to the surface tensions, the solidified nucleus has the shape of a cut-off sphere.
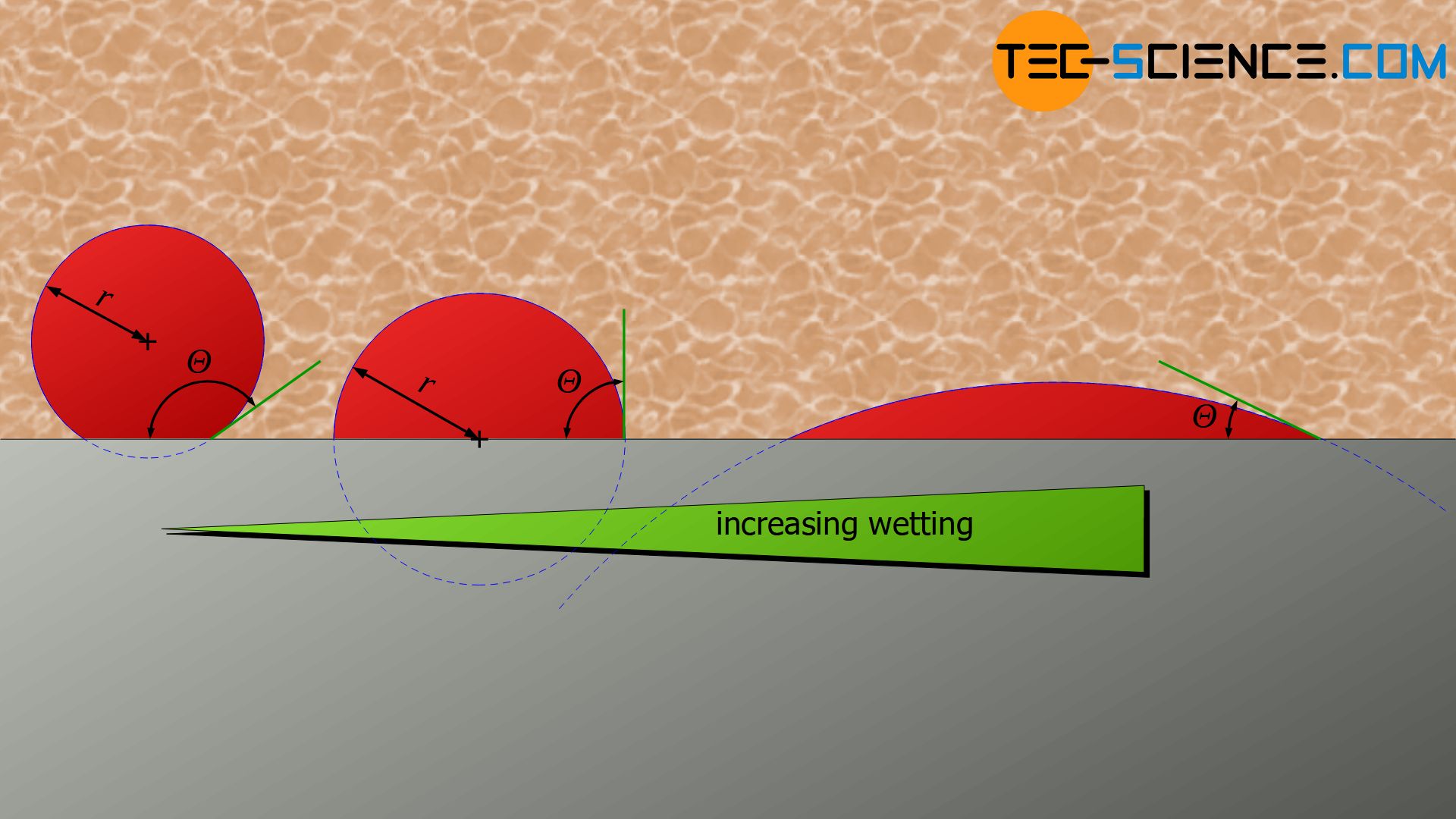
The angle at the contact point between the nucleus surface and the vessel wall is referred to as the contact angle \(\Theta\). Depending on the interaction between nucleus, melt and wall, the wall is very strongly wetted by the nucleus (small contact angle) or hardly wetted (large contact angle). This has a corresponding effect on the shape of the spherical cap.

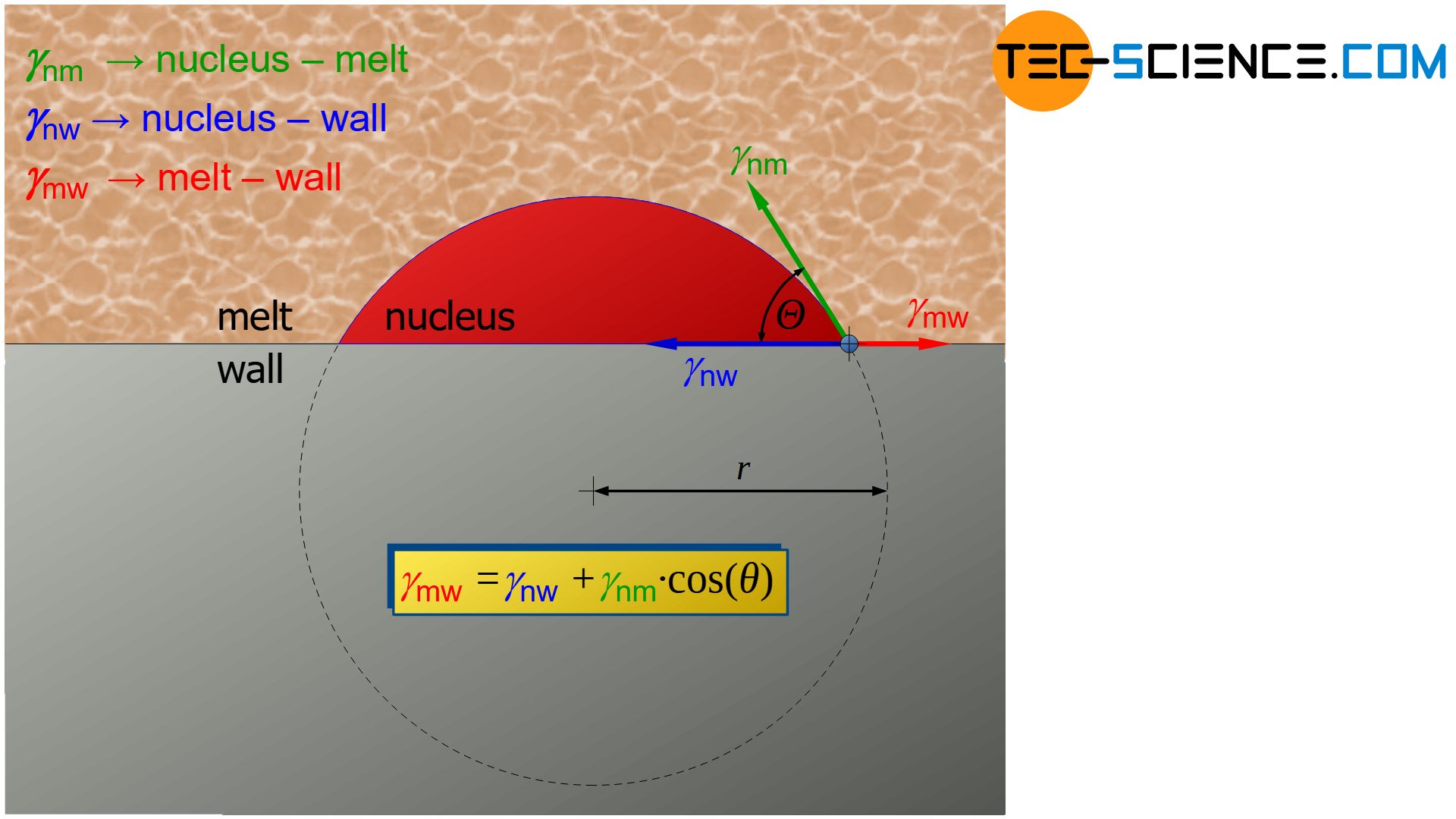
Decisive for the contact angle \(\Theta\) are the specific surface energies or surface tensions \(\gamma\) between the interfaces nucleus-melt (\(\gamma_{nm}\)), nucleus-wall (\(\gamma_{nw}\)) and melt-wall (\(\gamma_{mw}\)). From an equilibrium analysis, the following relationship results (Young relation):
\begin{align}
\label{benetzungswinkel}
\boxed{\cos\Theta = \frac{\gamma_{mw}-\gamma_{nw}}{\gamma_{nm}}} ~~~\text{Young relation} \\[5px]
\end{align}
Using the contact angle \(\Theta\), the volume \(V\) of the spherical cap at a given nucleus radius \(r\) can be determined by the following equation:
\begin{align}
&V= \tfrac{1}{3} h^2 \pi \left(3r – h \right) ~~~\text{with}~~~ h=r\left(1-\cos\Theta \right) ~~~\text{follows:} \\[5px]
\label{kuppelvolumen}
&\boxed{V= \tfrac{1}{3} \pi \left(2-3\cos\Theta+\cos^3\Theta \right)r^3} \\[5px]
\end{align}
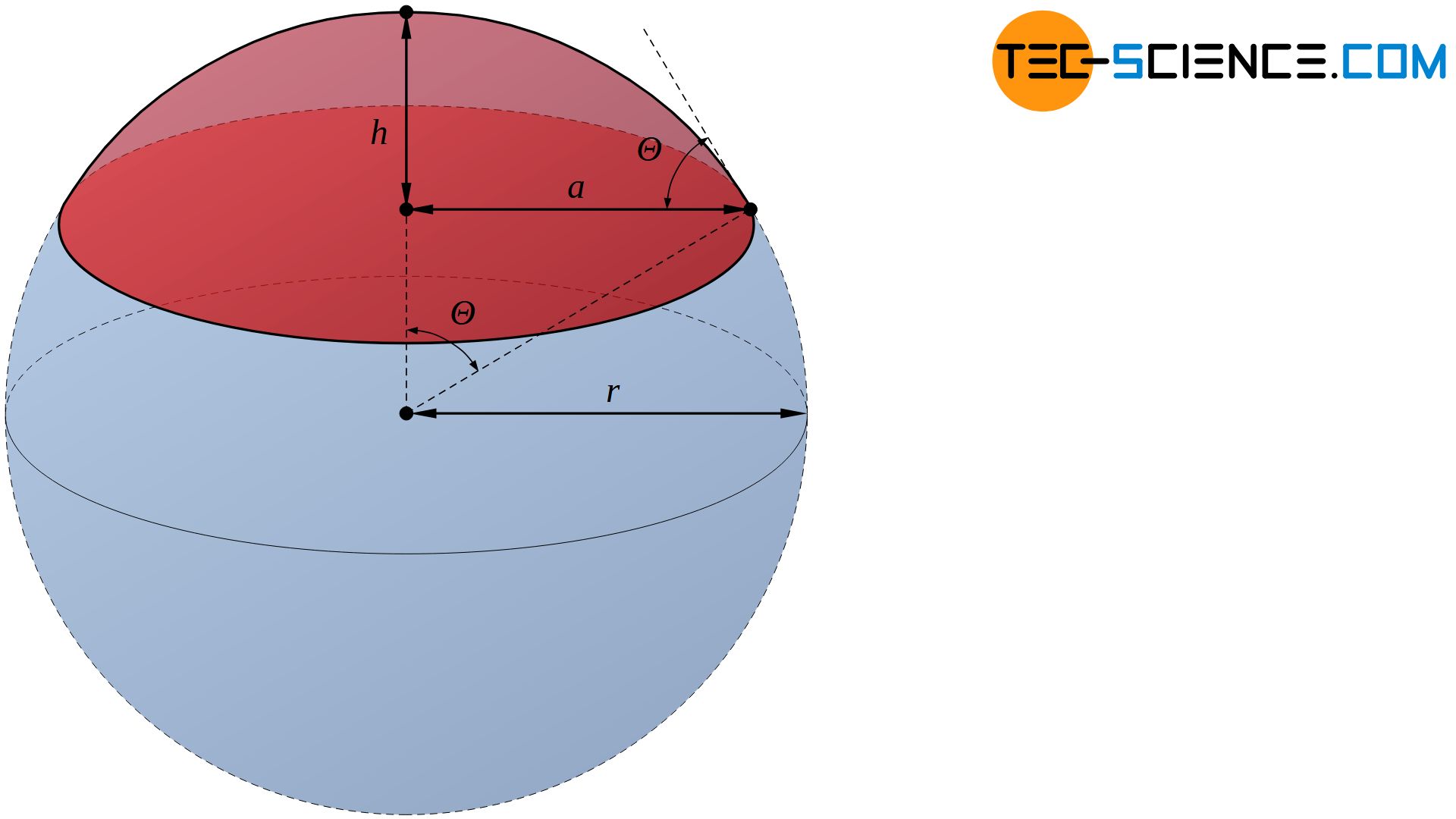
The contact angle \(\Theta\) can also be used to determine the surface of the spherical cap \(A_c\), which forms the interface between the nucleus and the melt:
\begin{align}
&A_c= 2\pi r h ~~~\text{with}~~~ h=r\left(1-\cos\Theta \right) ~~~\text{follows:} \\[5px]
\label{mantelflaeche}
&\boxed{A_c= 2 \pi \left(1-\cos\Theta \right) r^2} \\[5px]
\end{align}
The base surface \(A_w\) of the spherical segment that forms towards the wall also depends on the contact angle \(\Theta\):
\begin{align}
&A_w= \pi a^2 ~~~\text{with}~~~ a=r~\sin\Theta ~~~\text{follows:} \\[5px]
\label{basisflaeche}
&\boxed{A_w= \pi \sin^2\Theta \cdot r^2} \\[5px]
\end{align}
Gibbs energy of a nucleus
In the case of heterogeneous nucleation, the change in Gibbs energy \(\Delta G_n\) of a forming nucleus consists of three parts:
\begin{align}
\label{0}
\boxed{\Delta G_n = \Delta G_v + \Delta G_{s,nm} + \Delta G_{s,nw}}
\end{align}
- Reduction of volume energy \(\Delta G_v\) due to phase change
- Surface energy to be applied \(\Delta G_{s,nm}\) at the interface between nucleus and melt
- Change of surface energy \(\Delta G_{s,nw}\) during the phase change between nucleus and wall
These terms will be discussed in more detail below.
Reduction of volume energy due to phase change
The change in volume energy \(\Delta G_v\) is given by the volume \(V\) of the nucleus in combination with the density \(\rho\) and the specific Gibbs energy change \(\Delta g_v\) (Note that this part leads to a reduction of the energy and therefore bears a negative sign in contrast to the surface energy to be applied):
\begin{align}
&\Delta G_v = – m \cdot \Delta g_v ~~~~~\text{with}~~~~m = V \cdot \rho ~~~~ \text{follows:} \\[5px]
\label{321}
&\underline{\Delta G_v = – V \cdot \rho \cdot \Delta g_v } \\[5px]
\end{align}
The specific change in Gibbs energy \(\Delta g_v\) can be expressed by the relationship to the specific heat of solidification \(q_s\), solidification temperature \(T_s\) and undercooling \(\Delta T\) (derivation see here):
\begin{align}
\label{schmelz}
&\underline{\Delta g_v = q_s \cdot \frac{\Delta T}{T_s}} \\[5px]
\end{align}
If the equations (\ref{kuppelvolumen}) and (\ref{schmelz}) are entered in equation (\ref{321}), then the volume energy \(\Delta G_v\) to be applied results on the basis of a phase change of a nucleus as follows:
\begin{align}
\label{2}
&\boxed{\Delta G_v = – \frac{\pi~\rho~q_s}{3~T_s} \Delta T \left(2-3\cos\Theta+\cos^3\Theta \right) \cdot r^3} \\[5px]
\end{align}
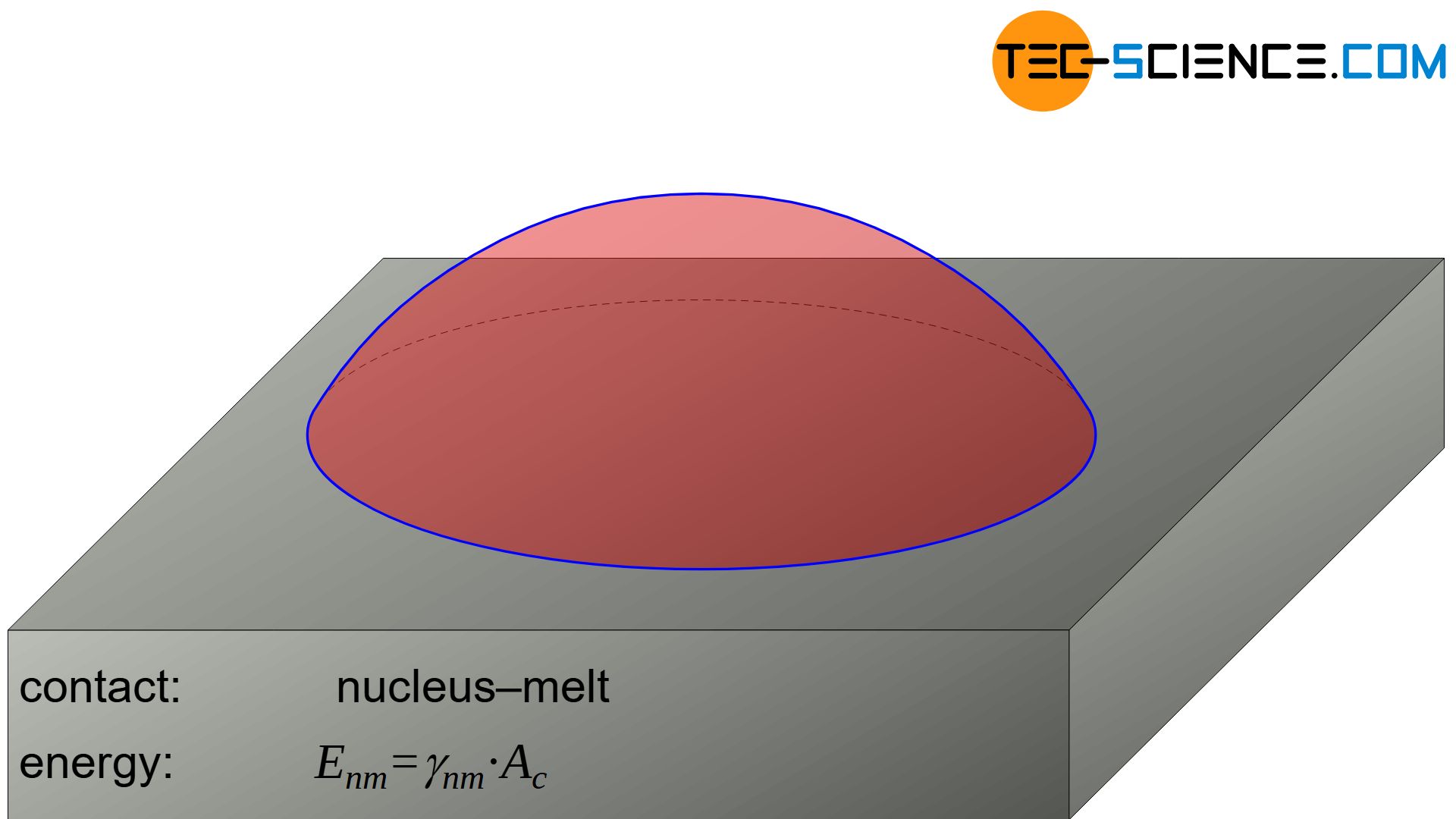
Surface energy to be applied at the interface between nucleus and melt
The surface energy \(\Delta G_{s,nm}\) to be applied to produce the nucleus surface towards the melt results via the spherical cap \(A_c\) and the corresponding specific surface energy \(\gamma_{nm}\):
\begin{align}
&\underline{\Delta G_{s,nm} = \gamma_{nm} \cdot A_c} \\[5px]
\end{align}
The surface energy \(\Delta G_{s,nm}\) to produce the nucleus surface towards the melt is given by means of equation (\ref{mantelflaeche}) as follows:
\begin{align}
\label{3}
&\boxed{\Delta G_{s,nm} = 2 \pi~\gamma_{nm}~\left(1-\cos\Theta \right) r^2} \\[5px]
\end{align}
Change of the surface energy at the interface to the wall
In the molten state, the surface energy \(E_{mw}\) is obtained at the contact surface between the not yet formed nucleus (= melt) and the wall as follows:
\begin{align}
E_{mw}=\gamma_{mw} \cdot A_w \\[5px]
\end{align}
Due to the formation of the nucleus, the surface energy \(E_{mw}\) between the former melt / wall changes to a different surface energy \(E_{nw}\) between nucleus / wall:
\begin{align}
E_{nw}=\gamma_{nw} \cdot A_w \\[5px]
\end{align}
As a result, the surface energy at the contact area with the wall – and with it Gibbs’ energy of the nucleus – has changed as follows:
\begin{align}
\label{d}
&\underline{\Delta G_{s,nw} = (\gamma_{nw}-\gamma_{mw}) \cdot A_w} \\[5px]
\end{align}
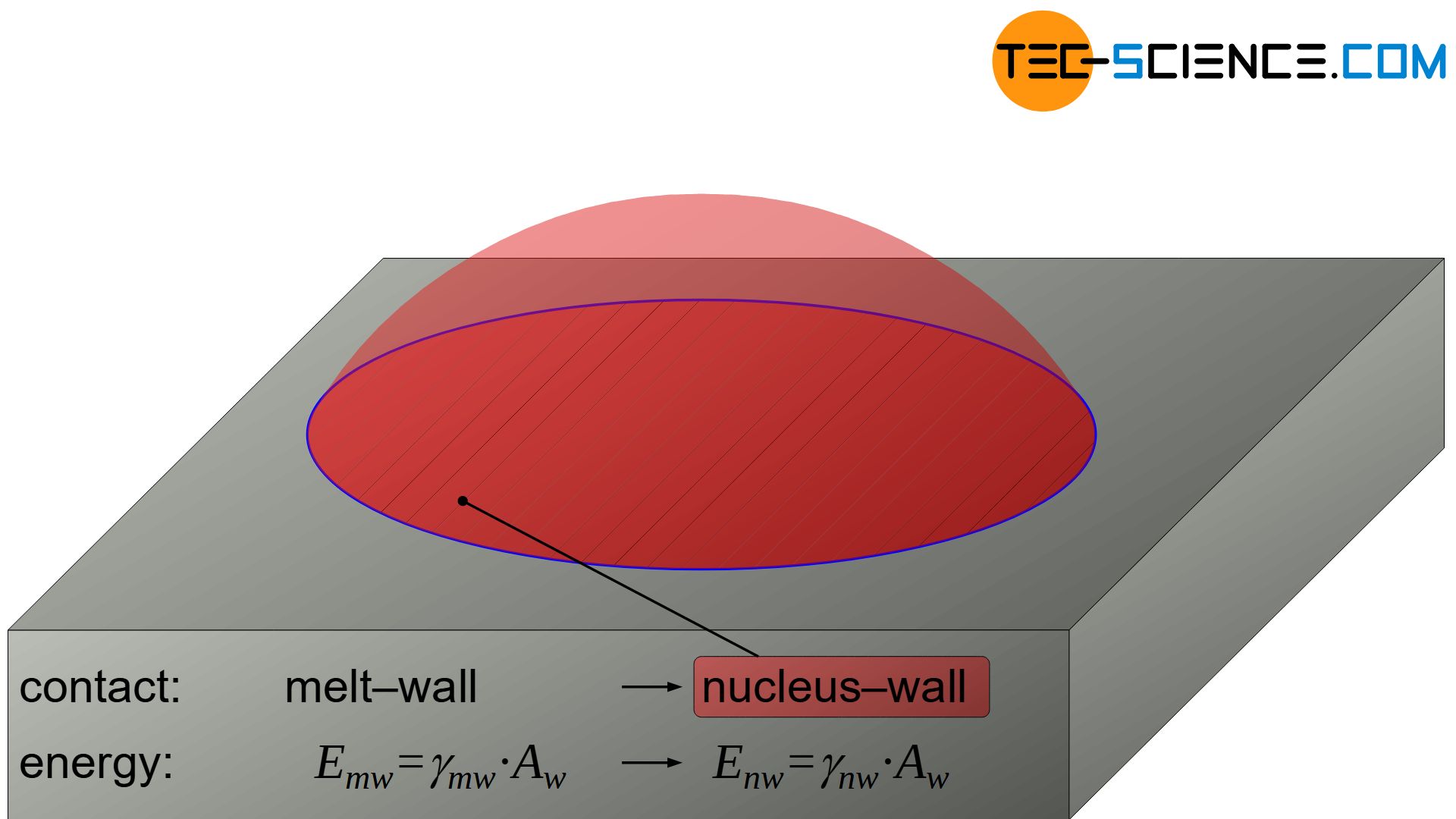
The energetic advantage of heterogeneous nucleation can already be seen at this point. The surface energy of the nucleus towards the wall does not have to be applied from zero but only has to change (\(\gamma_{mw}>0\))!
While the contact surface \(A_w\) is determined by the equation (\ref{basisflaeche}), the difference of surface tensions can be replaced by the equation (\ref{benetzungswinkel}):
\begin{align}
\label{young}
&\underline{\gamma_{nw}-\gamma_{mw} = -\gamma_{nm}\cdot \cos(\Theta)} \\[5px]
\end{align}
If equations (\ref{basisflaeche}) and (\ref{young}) are inserted into equation (\ref{d}), then change of a surface energy at a contact area to a wall \(\Delta G_{s,nw}\) can be calculated as follows:
\begin{align}
\underline{\Delta G_{s,nw} = -\gamma_{nm} \cdot \cos\Theta \cdot \pi \sin^2\Theta \cdot r^2} \\[5px]
\end{align}
Furthermore, the geometric expression \( \cos(\Theta) \cdot \sin^2(\Theta) \) can be replaced by the term \( \cos(\Theta) – \cos^3(\Theta) \). This finally leads to:
\begin{align}
\label{1}
&\boxed{\Delta G_{s,nw} = -\pi~\gamma_{nm}~ \left(\cos\Theta – \cos^3\Theta \right) \cdot r^2} \\[5px]
\end{align}
Total change of Gibbs energy of the germ
The change in Gibbs energy \(\Delta G_n\) of the solidifying nucleus can be expressed by inserting the equations (\ref{2}), (\ref{3}) and (\ref{1}) into equation (\ref{0}) and then summarizing as follows:
\begin{align}
\Delta G_n = &- \frac{\pi~\rho~q_s}{3~T_s} ~\Delta T \left(2-3\cos\Theta+\cos^3\Theta \right) \cdot r^3 \\[5px]
&+ 2 \pi~\gamma_{nm}~\left(1-\cos\Theta \right) r^2 \\[5px]
&- \pi~\gamma_{nm}~ \left(\cos\Theta – \cos^3\Theta \right) \cdot r^2 \\[5px]
\Delta G_n = &- \frac{\pi~\rho~q_s}{3~T_s} ~\Delta T \left(2-3\cos\Theta+\cos^3\Theta \right) \cdot r^3 \\[5px]
&+ \pi~\gamma_{nm}~\left( 2-3\cos\Theta+\cos^3\Theta \right) ~r^2 \\[5px]
\end{align}
By further summaries, the change in Gibbs energy of a wettening nucleus assumed to be spherical with the radius \(r\) at the given undercooling \(\Delta T\) can be represented as follows:
\begin{align}
\label{heterogene}
\boxed{\Delta G_n(\Delta T, r) =\tfrac{1}{4}\left(2-3\cos\Theta+\cos^3\Theta \right) ~ \left[-\tfrac{4~\pi~\rho~q_s}{3~T_s}~\Delta T~r^3 + 4\pi~\gamma_{nm}~r^2 \right]} \\[5px]
\end{align}
This equation is discussed in more detail in the following section.
Comparison of heterogeneous and homogeneous nucleation
A comparison with the energy change of a nucleus during homogeneous nucleation is interesting at this point:
\begin{align}
\label{keim}
&\boxed{\Delta G_{hom}(\Delta T, r) = -\tfrac{4 \pi \rho ~ q_s}{3 ~ T_S} \cdot \Delta T \cdot r^3 + 4 \pi ~ \gamma \cdot r^2} \\[5px]
\end{align}
With the same radius and same undercooling, the energy change by heterogeneous nucleation differs by the geometric factor located outside the square brackets of equation (\ref{heterogene}) (wetting factor).
The term inside the square brackets corresponds precisely to the change in energy during homogeneous nucleation. From an energetic point of view, the heterogeneous nucleation on a smooth wall is thus linked to the homogeneous nucleation as follows:
\begin{align}
\boxed{\Delta G_{het} =f(\Theta) \cdot \Delta G_{hom}} ~~~ \text{with} ~~~ \boxed{f(\Theta)=\tfrac{1}{4}\left(2-3\cos\Theta+\cos^3\Theta \right)} \le 1 \\[5px]
\end{align}
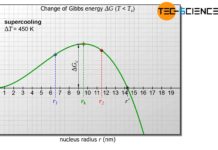
The critical nucleation radius is basically the same for heterogeneous nucleation as for homogeneous nucleation, only the activation energies differ (under otherwise identical conditions). Note that the heterogeneous nucleation has the same (fictitious) nucleus radius, but ultimately only part of the sphere volume actually forms the actual nucleus.
The critical nucleus radius can in principle be obtained in the same way as for homogeneous nucleation by deriving and zeroing the equation (\ref{heterogene}):
\begin{align}
&\frac{d (\Delta G_n)}{dr} = 0 \\[5px]
& \tfrac{1}{4}\left(2-3\cos\Theta+\cos^3\Theta \right) \cdot \left[-\tfrac{4 \pi \rho ~ q_s}{T_s} \cdot \Delta T \cdot r^2 + 8 \pi \gamma_{nm} \cdot r \right] = 0 \\[5px]
& \frac{4 \pi \rho ~ q_s}{T_s} \cdot \Delta T \cdot r = 8 \pi \gamma_{nm} \\[5px]
& \boxed{r_{c,het} = \frac{2 \gamma_{nm} ~ T_s}{q_s~ \rho ~\Delta T}}=r_{c,hom}
\end{align}
Insertion of the critical radius \(r_{c,het}\) in equation (\ref{heterogene}) provides the activation energy of heterogeneous nucleation \(\Delta G_{c,het}\) (free energy barrier), with the already described correlation to homogeneous nucleation:
\begin{align}
&\boxed{\Delta G_{c,het} = \tfrac{1}{4}\left(2-3\cos\Theta+\cos^3\Theta \right) \cdot \left[\frac{16 ~\pi ~ \gamma_{nm}^3 ~ T_s^2}{3 ~ q_s^2 ~ \rho^2 ~ \Delta T^2}\right] } \\[5px]
\end{align}
or
\begin{align}
&\boxed{\Delta G_{c,het} = f(\Theta) \cdot \Delta G_{c,hom}} ~~~ \text{with} ~~~ \boxed{f(\Theta)=\tfrac{1}{4}\left(2-3\cos\Theta+\cos^3\Theta \right)} \le 1 \\[5px]
\end{align}
The term, which is purely dependent on the contact angle, is always less than 1, so that it becomes apparent at this point that the heterogeneous nucleation requires less activation energy than the homogeneous nucleation.
For a contact angle of \(\Theta\)=90° the nucleus is a hemisphere and the wetting factor has the value \(f(\Theta)\)=0.5. In this case, the nucleus requires only half the activation energy. After all it has only half as much volume as a spherical nucleus during homogeneous nucleation.
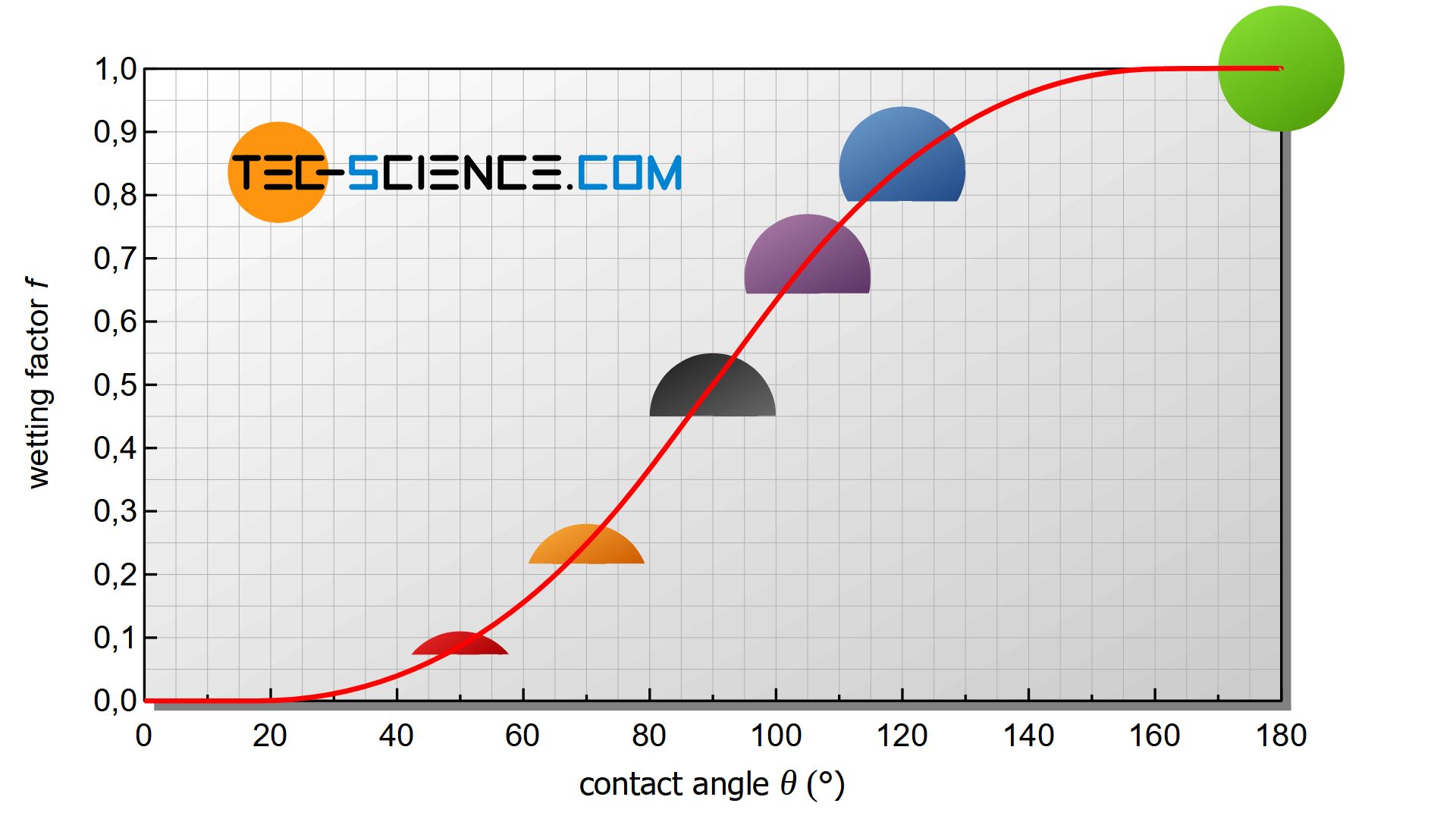
With larger contact angles, the wetting factor increases more and more. At an angle of \(\Theta\)=180°, the wetting factor finally reaches its maximum of 1. the spherical cap has become a complete sphere that no longer wet the wall. As a special case, the homogeneous nucleation is then obtained!
Conversely, very small wetting factors are obtained for small contact angles, i.e. for very strong wetting. As a result, the activation energy required for nucleation is greatly reduced. With a smaller contact angle and the same critical radius, the volume of the nucleus also decreases considerably. It will then no longer be necessary to provide as many atoms for nucleation.
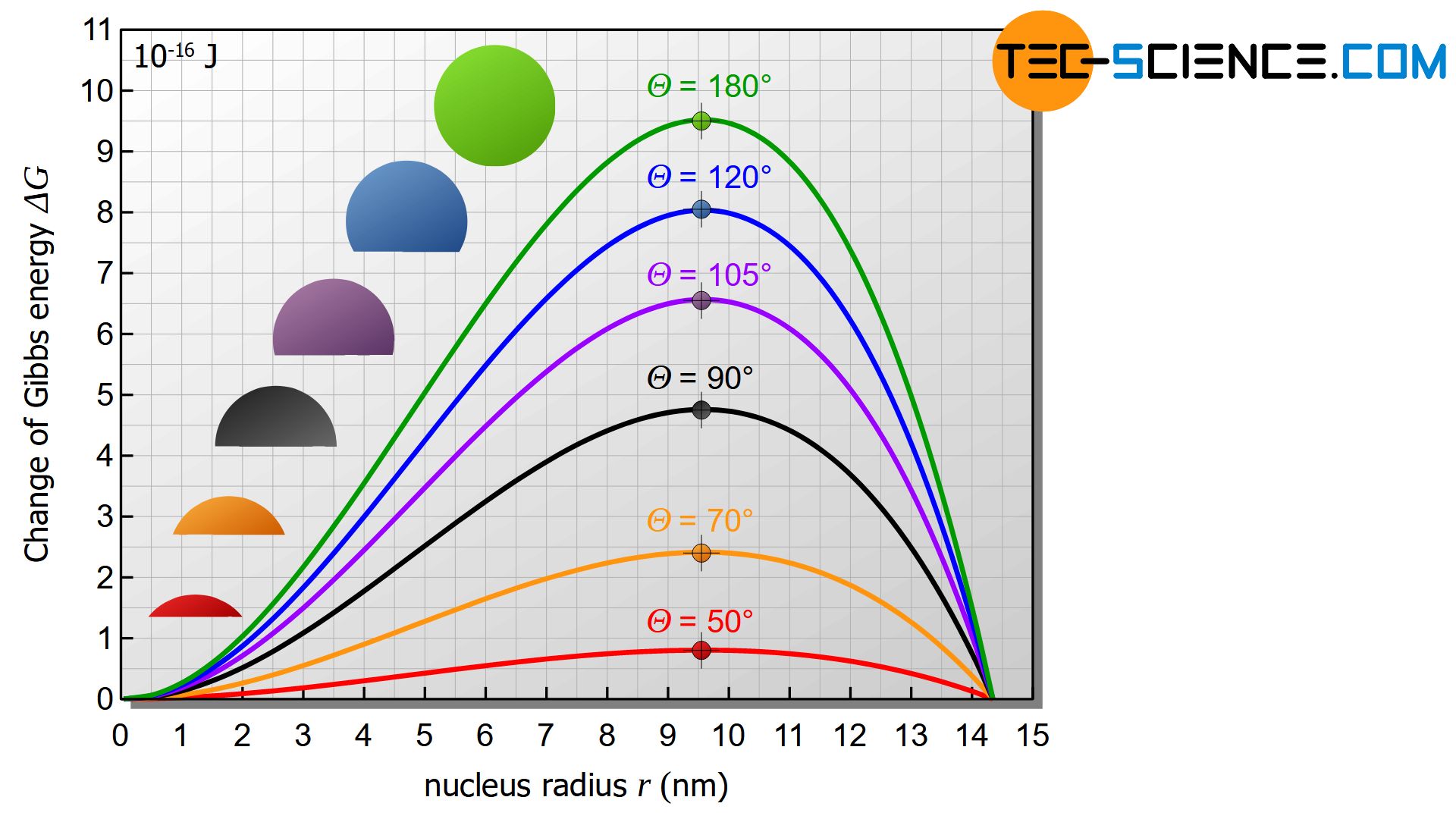
At a contact angle of \(\Theta\)=20°, for example, the required number of atoms drops from 300,000 atoms to only 800 atoms (under otherwise identical conditions) compared to the example already presented for homogeneous nucleation.
The activation energy decreases by the same factor from the original 9.5⋅10-16 J to 0.025⋅10-16 J. Thus it becomes clear once again that heterogeneous nucleation is much more likely than homogeneous nucleation.
The heterogeneous nucleation works particularly well if the introduced foreign particles (seed crystals) or the vessel walls can be wetted very well.
When introducing seed crystals into the melt, make sure that the seed particles have a larger radius than the critical radius of nucleation. At the same time, however, there is a risk that the particles could dissolve in the hot melt before nucleation could have begun. For this reason, the seed crystals are often introduced directly into the undercooled melt during pouring.