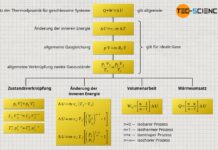
Erfahre in diesem Artikel mehr über die Berechnung der inneren Energie für ideale Gase.
Erster Hauptsatz der Thermodynamik
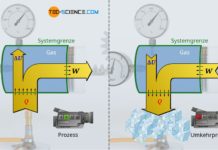
Im Artikel Innere Energie von idealen Gasen wurde ausführlich erläutert, dass bei idealen Gasen nur die Bewegungsenergie der Gasteilchen als innere Energie existiert (thermische Energie). Diese innere Energie lässt sich gemäß dem ersten Hauptsatz der Thermodynamik durch eine Energiezufuhr oder -abfuhr in Form von Arbeit W oder Wärme Q ändern:
\begin{align}
&\boxed{\Delta U = W + Q } ~~~~~\text{Änderung der inneren Energie} \\[5px]
\end{align}
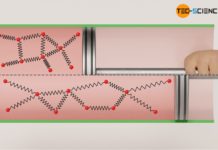
Die Bewegungsenergie der Teilchen ist gemäß der Maxwell-Boltzmann-Verteilung wiederum direkt mit der Temperatur verknüpft. Somit führt eine Änderung der inneren Energie (Änderung der Bewegungsenergie) unweigerlich zu einer Änderung der Temperatur. Es stellt sich dabei die Frage, welche Gesetzmäßigkeiten zwischen der Änderung der inneren Energie ΔU und der Temperaturänderung ΔT zugrunde liegen.
Vorüberlegungen zur Bestimmung der Änderung der inneren Energie
Wie bereits erwähnt, zeigt die kinetische Gastheorie einen direkten Zusammenhang zwischen der mittleren Bewegungsenergie der Teilchen in einem Gas und dessen Temperatur. Kennt man also die Temperatur eines Gases (und die Anzahl der Teilchen), dann ist damit direkt eine bestimmte innere Energie verbunden. Dies ist unabhängig vom Druck oder vom Volumen des Gases. Somit ist die Änderung der inneren Energie auch nur von der Änderung der Temperatur abhängig.
Die Änderung der inneren Energie während eines thermodynamischen Prozesses ist bei idealen Gasen also eindeutig bestimmt, wenn man die Anfangstemperatur (und damit die Anfangsenergie) und Endtemperatur (und damit die Endenergie) kennt. Auf welchem Prozessweg das Gas nun genau von seiner Anfangstemperatur zu seiner Endtemperatur gelangt, ist für die Änderung der damit verbundenen inneren Energie irrelevant. Ob es sich dabei um einen isobaren, isochoren, isentropen oder sonst einem beliebigen Prozess handelt, spielt folglich für die Änderung der inneren Energie überhaupt keine Rolle. Nur die jeweils vollzogene Temperaturänderung bestimmt die Änderung der inneren Energie!
Die Tatsache, dass die innere Energie nur vom Zustand des Gases (in Form der Temperatur) abhängig ist und nicht von der Art des Prozesses, macht die innere Energie zu einer Zustandsgröße. Im Gegensatz hierzu hängen Wärme und Arbeit vom genaueren Prozess ab (ob isochor, isotherm, isobar oder isentrop) und zählen deshalb zu den Prozessgrößen.
Möchte man also den Zusammenhang zwischen Änderung der inneren Energie und Temperaturänderung untersuchen, dann kann dies prinzipiell an einem beliebigen Prozess erfolgen. Die bei diesem Prozess gewonnene Erkenntnis gilt dann für jeden beliebigen Prozess auch, d.h. ganz allgemein für ideale Gase. Zur Untersuchung der Zusammenhänge bietet sich der isochore Prozess besonders an, da bei einem solchen Prozess keine Arbeit verrichtet wird. Eine Wärmezufuhr kommt damit vollständig der inneren Energie zugute und ist somit relativ einfach untersuchbar. Im nächsten Abschnitt wird hierauf näher eingegangen.
Herleitung am Beispiel eines isochoren Prozesses
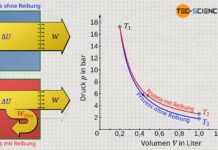
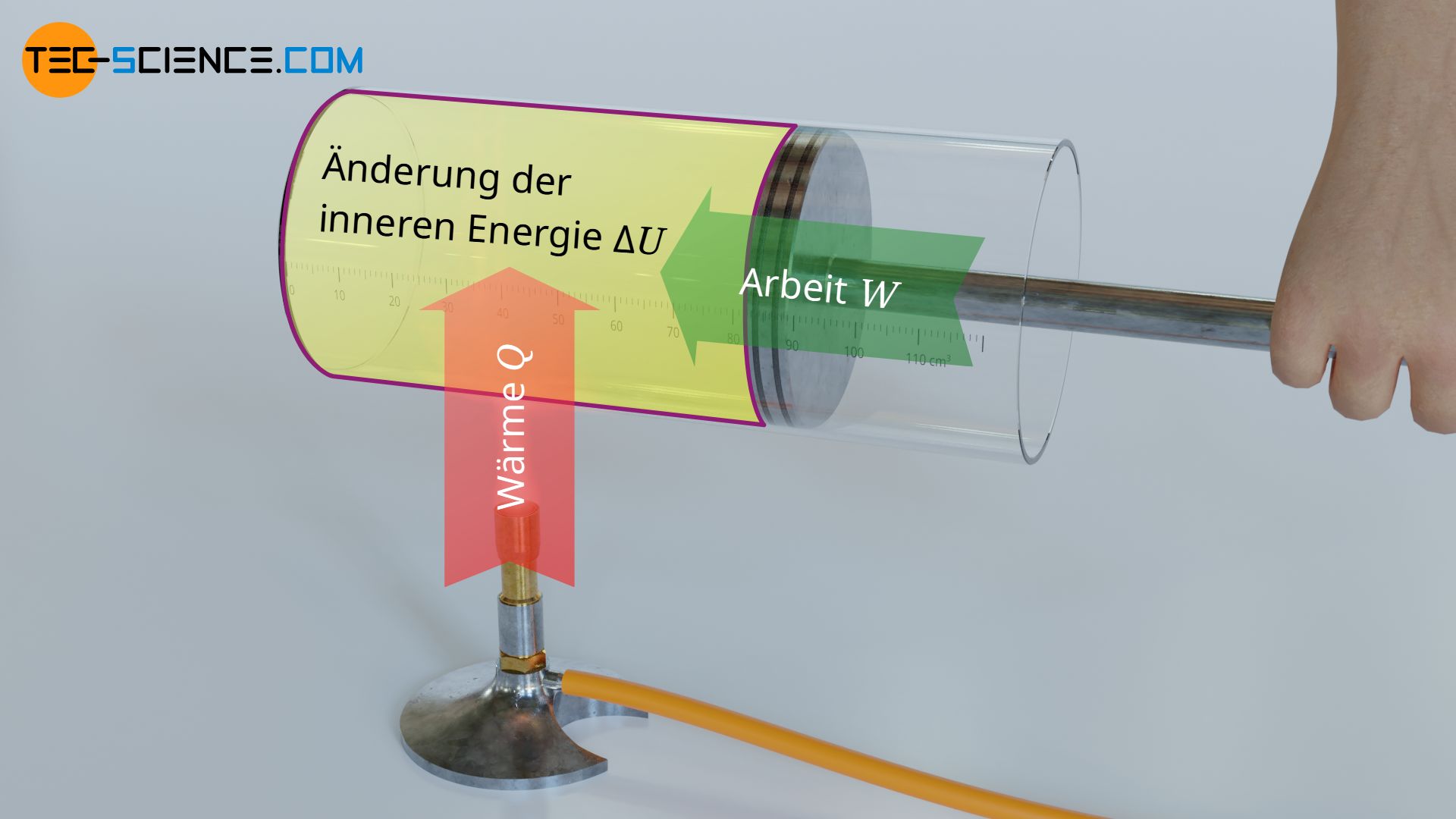
Zur Bestimmung des Zusammenhangs zwischen Änderung der inneren Energie und Temperaturänderung wird folgendes Experiment betrachtet. Ein Gas der Masse m ist in einem Zylinder mit konstantem Volumen fest eingeschlossen. Durch Wärmezufuhr steigt die Temperatur des Gases und mit ihr die innere Energie.

Da sich das Volumen bei einem solchen isochoren Prozess nicht ändern kann, ist ein Arbeitsumsatz auf mechanischem Wege durch Expansion oder Kompression ausgeschlossen (W=0). Gemäß des ersten Hauptsatzes findet sich die Wärmezufuhr Q damit vollständig in der Änderung der inneren Energie ΔU wieder:
\begin{align}
& \Delta U = \underbrace{W}_{=0}+Q= Q \\[5px]
\label{u}
& \underline{\Delta U = Q} \\[5px]
\end{align}

Um den Einfluss der Änderung der inneren Energie auf die Änderung der Temperatur zu ermitteln, müssen also nicht aufwendige Untersuchungen zur Bewegungsenergie der einzelnen Teilchen angestellt werden. Gemäß Gleichung (\ref{u}) genügt es den wesentlich einfacher zu untersuchende Zusammenhang zwischen einer Wärmezufuhr Q (die dann direkt der Änderung der inneren Energie ΔU entspricht) und der resultierenden Temperaturerhöhung ΔT eines isochoren Prozesses zu untersuchen. Die zugeführte Energie kann bspw. über die elektrische Leistung eines Heizgerätes relativ einfach bestimmt werden („Wärme = elektrische Leistung x Zeit“).
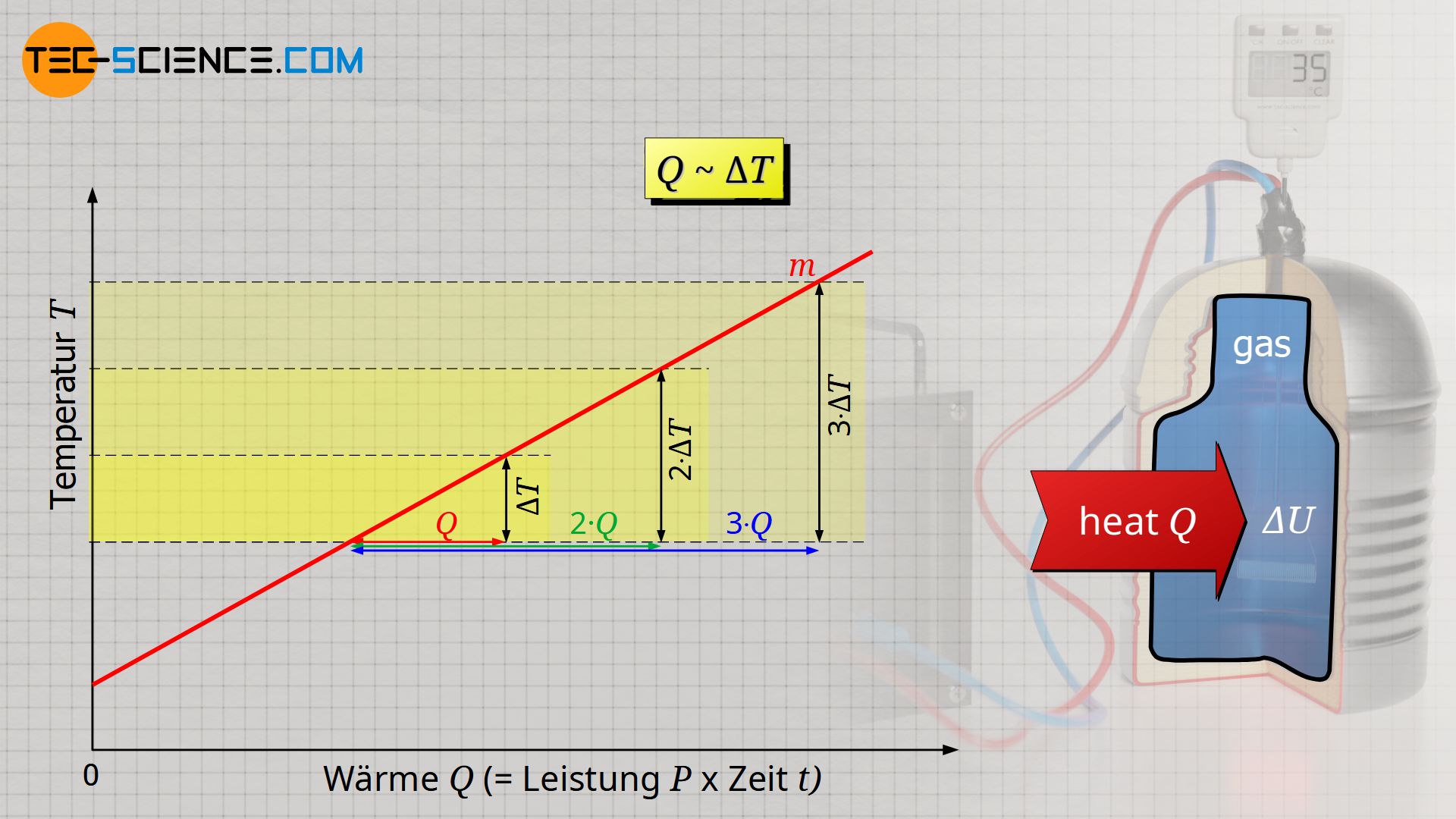
Dabei zeigt sich, dass die Temperaturänderung ΔT proportional zur zugeführten Wärme Q ist, d.h. eine doppelte Temperaturänderung erfordert auch eine doppelt so große Wärmezufuhr:
\begin{align}
\label{q}
& Q \sim \Delta T \\[5px]
\end{align}
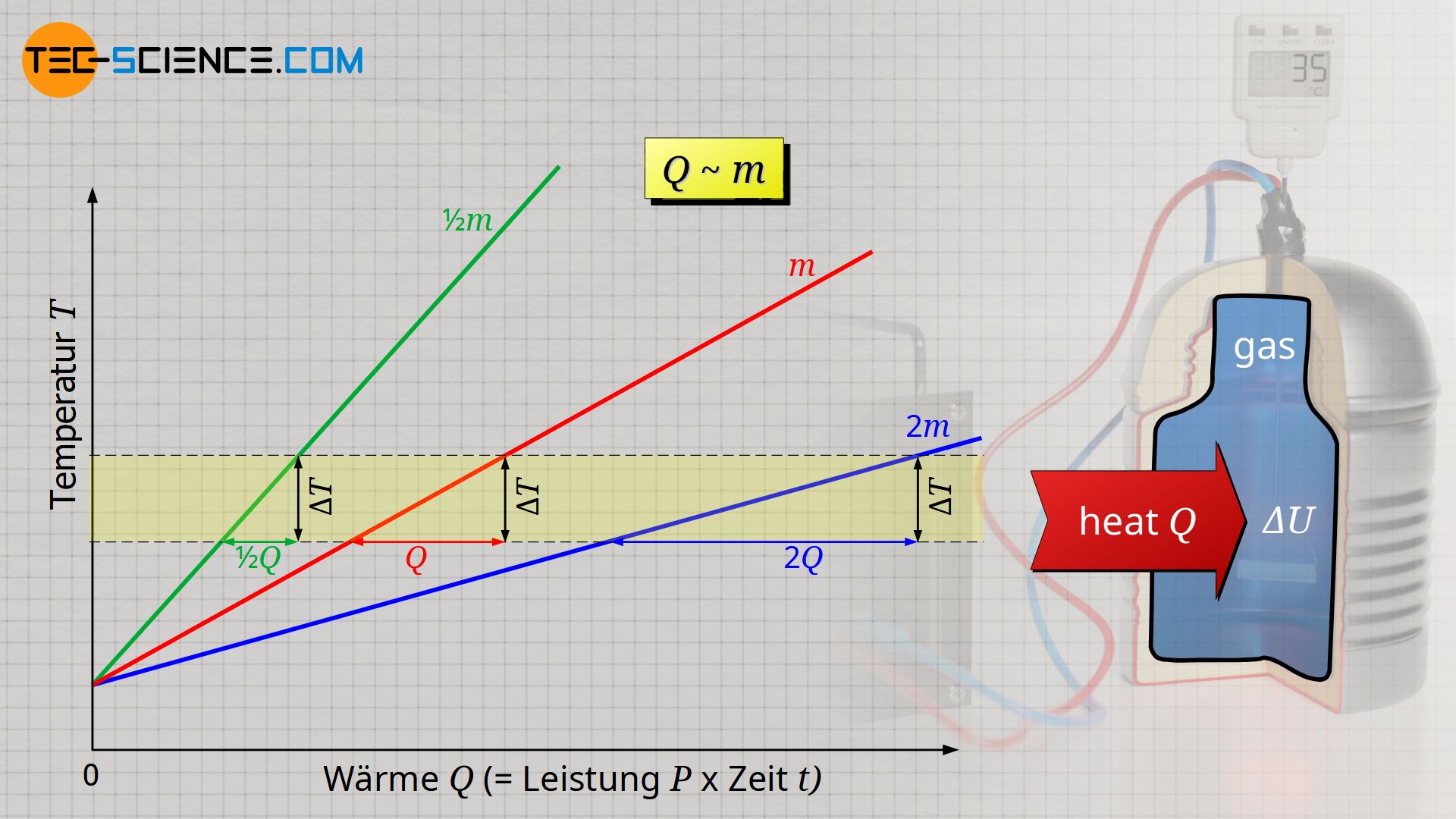
Des Weiteren stellt man fest, dass umso mehr Wärme erforderlich wird, umso größer die zu erwärmende Gasmasse ist. Für eine doppelt so große Masse, ist auch eine doppelt so große Wärmeenergie Q notwendig, um sie dementsprechend zu erwärmen. Wärme Q und Masse m sind damit ebenfalls proportional zueinander:
\begin{align}
\label{m}
& Q \sim m \\[5px]
\end{align}
Insgesamt betrachtet ist also die (zugeführte) Wärme Q proportional zur Masse m und zur Temperaturänderung ΔT. Der Proportionalitätsfaktor zwischen diesen Größen wird als spezifische Wärmekapazität cv bezeichnet und ist eine Stoffkonstante, die im Idealfall nicht von der Temperatur abhängig ist, sondern nur von der Gasart:
\begin{align}\;\;\;\;\;
& Q \sim m \cdot \Delta T \\[5px]
\label{c}
& \underline {Q = c_\text{v} \cdot m \cdot \Delta T} ~~~~~ [c_\text{v}]=\frac{\text{J}}{\text{kg} \cdot \text{K}} ~~~\text{spezifische Wärmekapazität} \\[5px]
\end{align}
Die spezifische Wärmekapazität gibt anschaulich an wie viel Energie notwendig ist, um die Temperatur eines Stoffes der Masse 1 kg um 1 K zu erwärmen. Oder in diesem Fall: Um welchen Betrag sich die innere Energie pro Kilogramm Gasmasse ändert, wenn sich die Temperatur um 1 K ändert. Gemäß Gleichung (\ref{u}) ist nun der gesuchte Zusammenhang zwischen der Änderung der inneren Energie ΔU und der Temperaturänderung ΔT für ein ideales Gas gefunden:
\begin{align}\;\;\;\;\;
\label{d}
& \boxed{ \Delta U = c_\text{v} \cdot m \cdot \Delta T} ~~~\text{mit } \Delta T = T_2-T_1~~~\text{gilt allgemein für ideale Gase!} \\[5px]
\end{align}
An dieser Stelle sei nochmals ausdrücklich erwähnt, dass dieser Zusammenhang zwischen der Änderung der inneren Energie und der Temperaturänderung nicht nur für isochore Prozesse gilt, sondern für jeden beliebigen Prozess eines idealen Gases! An dieser Stelle muss man sich klar machen, dass die innere Energie eben keine Prozessgröße wie Arbeit und Wärme ist, sondern eine Zustandsgröße, die nur durch die Temperatur bestimmt ist. Denn alleine die Temperatur entscheidet gemäß der Maxwell-Boltzmann-Verteilung über die Energie eines Teilchen und damit – unter Berücksichtigung der Gesamtheit der Teilchen in Form der Gasmasse – über die innere Energie des gesamten Gases.
Anmerkung zur Formel
An dieser Stelle darf man sich nicht durch die (missverständliche) Begrifflichkeit der „spezifischen Wärmekapazität des isochoren Prozesses“ cv beirren lassen, die in der allgemeingültigen Formel (\ref{d}) auftaucht. Im Zusammenhang mit der Änderung der inneren Energie handelt es sich bei dem cv-Wert in erster Linie lediglich um eine Proportionalitätskonstante zwischen der Änderung der Inneren Energie und der Temperaturänderung.
Diese Proportionalitätskonstante wird nur deshalb als Wärmekapazität des isochoren Prozesses bezeichnet, da sie für den isochoren Prozess (und nur für den isochoren Prozess!) nämlich gleichzeigt den Wärmeumsatz beschreibt – siehe Gleichung (\ref{c}). Aus diesem Grund ist auch der Zusatz „v, für den isochoren Prozess stehend, im Index hinzugefügt. Diese Einschränkung gilt allerdings nur für den Wärmeumsatz, nicht jedoch für die Änderung der inneren Energie.
Für die Änderung der inneren Energie gilt Gleichung (\ref{d}) also für jedes ideale Gas gleichermaßen und bleibt nicht auf den isochoren Prozess beschränkt! Man sollte sich an dieser Stelle nicht durch Index „v“ in Gleichung (\ref{d}) täuschen lassen und der Meinung verfallen, dass diese Gleichung nur für den isochoren Prozess gilt.
Innere Energie von idealen Gasen
Auch wenn in der Thermodynamik häufig nur die Änderung der inneren Energie ΔU relevant ist, so kann für ideale Gase auch die innere Energie U selbst ermittelt werden. Hierzu stelle man sich ein Gas in einem Zylinder vor, das im Ausgangzustand zunächst bis auf den absoluten Nullpunkt heruntergekühlt ist. In diesem Zustand sind alle Teilchen in Ruhe und das Gas besitzt folglich keinerlei innere Energie. Nun wird dem Gas isochor die Wärmeenergie Q zugeführt bis dieses im Endzustand die Temperatur T erreicht hat. Die gesamt zugeführte Wärme, die nötig war, um das Gas bis zu dieser Temperatur T zu erwärmen, findet sich schließlich als innere Energie U wieder. Somit trägt das Gas bei dieser Temperatur T die folgende innere Energie U:
\begin{align}
\label{t}
& \boxed{ U = c_v \cdot m \cdot T} ~~~\text{gilt allgemein für perfekte Gase!} \\[5px]
\end{align}
Anmerkung: Strenggenommen kann die spezifische Wärmekapazität cv auch für ideale Gase von der Temperatur abhängig sein. Nämlich dann, wenn mit sinkender Temperatur durch quantenmechanische Effekte Freiheitsgrade eingefroren werden. Die Gleichungen (\ref{d}) und (\ref{t}) gelten dann nicht mehr uneingeschränkt. Wird aber vorausgesetzt, dass eine solche Temperaturabhängigkeit nicht existiert, dann spricht man häufig auch von perfekten Gasen und die Gleichungen (\ref{d}) und (\ref{t}) gelten uneingeschränkt.
Analogie zwischen innerer Energie und Lageenergie
Die innere Energie lässt sich für ideale Gase sehr anschaulich mit der Lageenergie eines Gegenstandes vergleichen. So stellt die Lageenergie den energetischen (Lage-)Zustand eines Körpers bei einer bestimmten Höhe h dar. Auf die analoge Weise gibt die innere Energie den energetischen (Bewegungs-)Zustand eines idealen Gases bei einer bestimmten Temperatur T wieder.
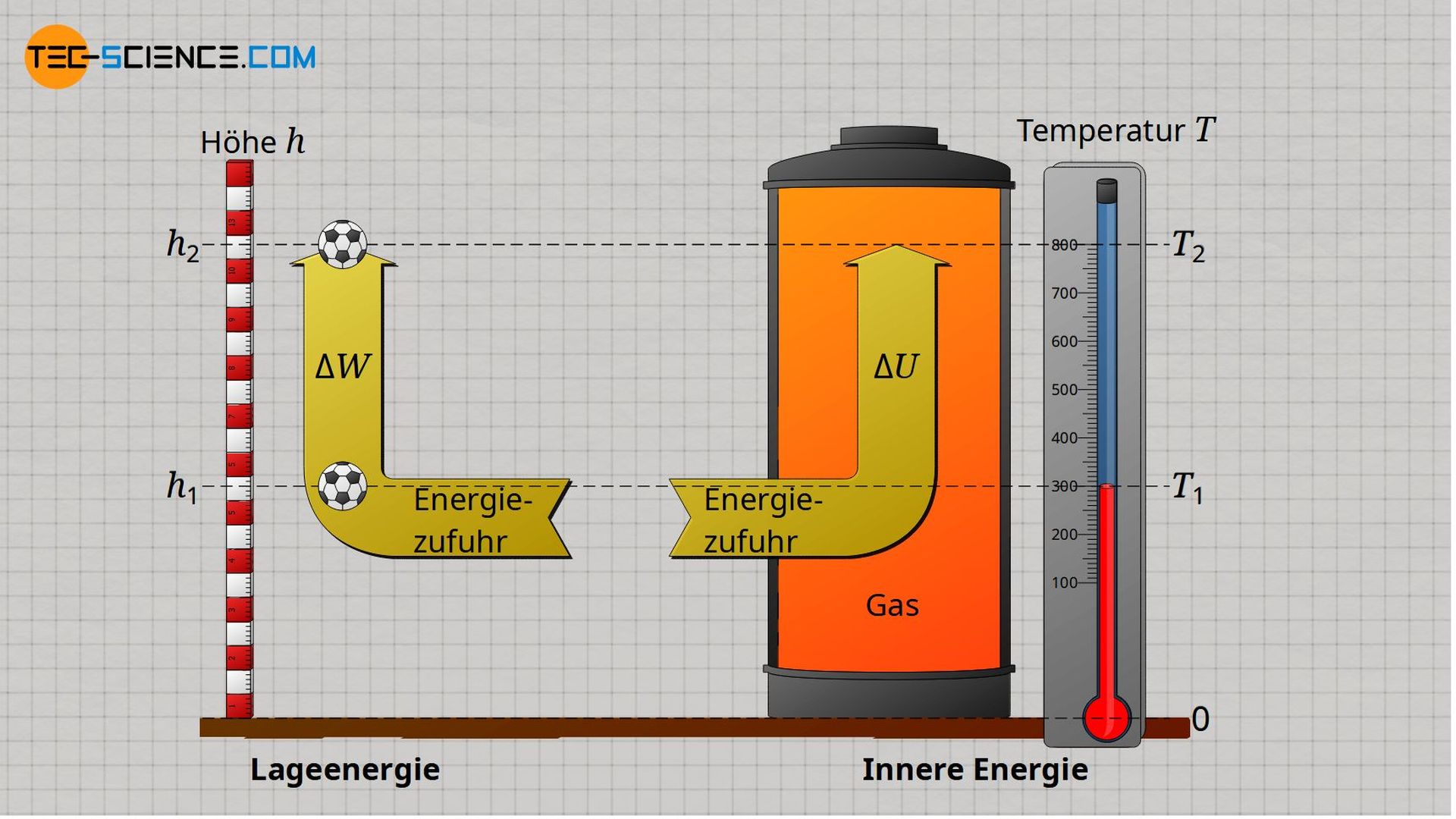
Einer bestimmen Höhe h lässt sich dabei über die Masse m des Körpers eine eindeutige Lageenergie zuordnen. Auf die analoge Weise lässt sich einer bestimmten Temperatur T über die Masse m des Gases eine bestimmte innere Energie zuschreiben. Der konkrete Zusammenhang zwischen Lageenergie und Höhe h wird dabei über die Fallbeschleunigung g (ortsabhängig!) hergestellt. Im Fall der inneren Energie wird der Zusammenhang zur Temperatur T über die spezifische Wärmekapazität cv vorgenommen (stoffabhängig!).
| Lageenergie | Innere Energie |
|---|---|
| Höhe h | Temperatur T |
| Masse des Körpers m | Masse des Gases m |
| Fallbeschleunigung g | Spezifische Wärmekapazität cv |
| Lageenergie W = m⋅g⋅h | Innere Energie U = m⋅cv⋅T |
| Änderung der Lageenergie ΔW = m⋅g⋅Δh | Änderung der inneren Energie ΔU = m⋅cv⋅ΔT |
Der energetische Zustand des auf einer Höhe h befindlichen Körpers kann durch Aufwendung von Energie geändert werden – er kann auf eine neue Höhe gebracht werden. Auf die analoge Weise lässt sich der energetische Zustand eines Gases durch Aufwendung von Energie ändern – es kann auf eine neue Temperatur gebracht werden.
Die aufzuwendende Energie um einen Körper von einer Höhe h1 auf eine Höhe h2 zu befördern ist nur von der Höhendifferenz Δh = h2 – h1 abhängig und nicht vom Prozessweg! Ebenso ist die aufzuwendende Energie um ein ideales Gas von der Temperatur T1 auf eine Temperatur T2 zu bringen nur von der Temperaturdifferenz ΔT = T2 – T1 abhängig und nicht vom Prozessweg.