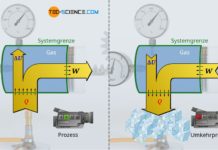
Das Gesetz von Amontons beschreibt die Zunahme des Druck bei zunehmender Temperatur für eine Zustandsänderung bei konstantem Volumen (isochorer Prozess).
Isochore Zustandsänderung
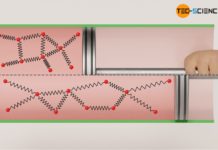
Erfolgen thermodynamische Prozesse bei konstantem Volumen, so werden diese auch als isochore Zustandsänderungen bezeichnet. Eine solche isochore Zustandsänderung eines Gases liegt bspw. bei Reifen oder Gasflaschen vor, die durch Sonneneinstrahlung erwärmt werden. Das Gasvolumen ist dabei alleine durch die Form des Reifens bzw. der Flasche bestimmt, die sich während der Zustandsänderung (fast) nicht ändert. Die Alltagserfahrung zeigt dabei, dass bei einer solchen isochoren Temperaturerhöhung der Druck ansteigt. Die genauere Abhängigkeit des Gasdrucks vom Volumen während einer solchen isothermen Zustandsänderung eines geschlossenen Systems soll im Folgenden näher untersucht werden.

Experimentelle Untersuchung
Zur Untersuchung der Zusammenhänge wird ein Glaskolben verwendet, der mit einem Korken fest verschlossen ist. Das eingeschlossene Gasvolumen bleibt somit stets konstant. Als Gas wird Luft verwendet, das näherungsweise als ideales Gas betrachtet werden kann. Mit Hilfe eines Druckmessers wird der Druck im Glaskolben als Absolutdruck bestimmt. Zusätzlich befindet sich ein Thermometer am Glaszylinder, mit dem die Gastemperatur gemessen wird.

Das Einstellen der Gastemperatur erfolgt durch Erwärmung des Glaskolbens in einem Wasserbad. Der je nach Temperatur resultierende Druck, wird am Druckmesser abgelesen. Auf diese Weise kann die Abhängigkeit des Druck von der Temperatur bei konstantem Volumen untersucht werden.
Linearität zwischen Druck und Temperatur (Einheit: Grad Celsius)
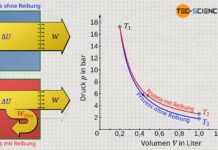
Bereits während des Versuchs stellt man fest, dass der Druck umso größer ist, je höher die Temperatur ist. Für eine genauere Analyse ist es sinnvoll die Messwerte in ein Schaubild einzutragen. Hierzu wird der Druck (in bar) in Abhängigkeit der Temperatur (in °C) aufgetragen.
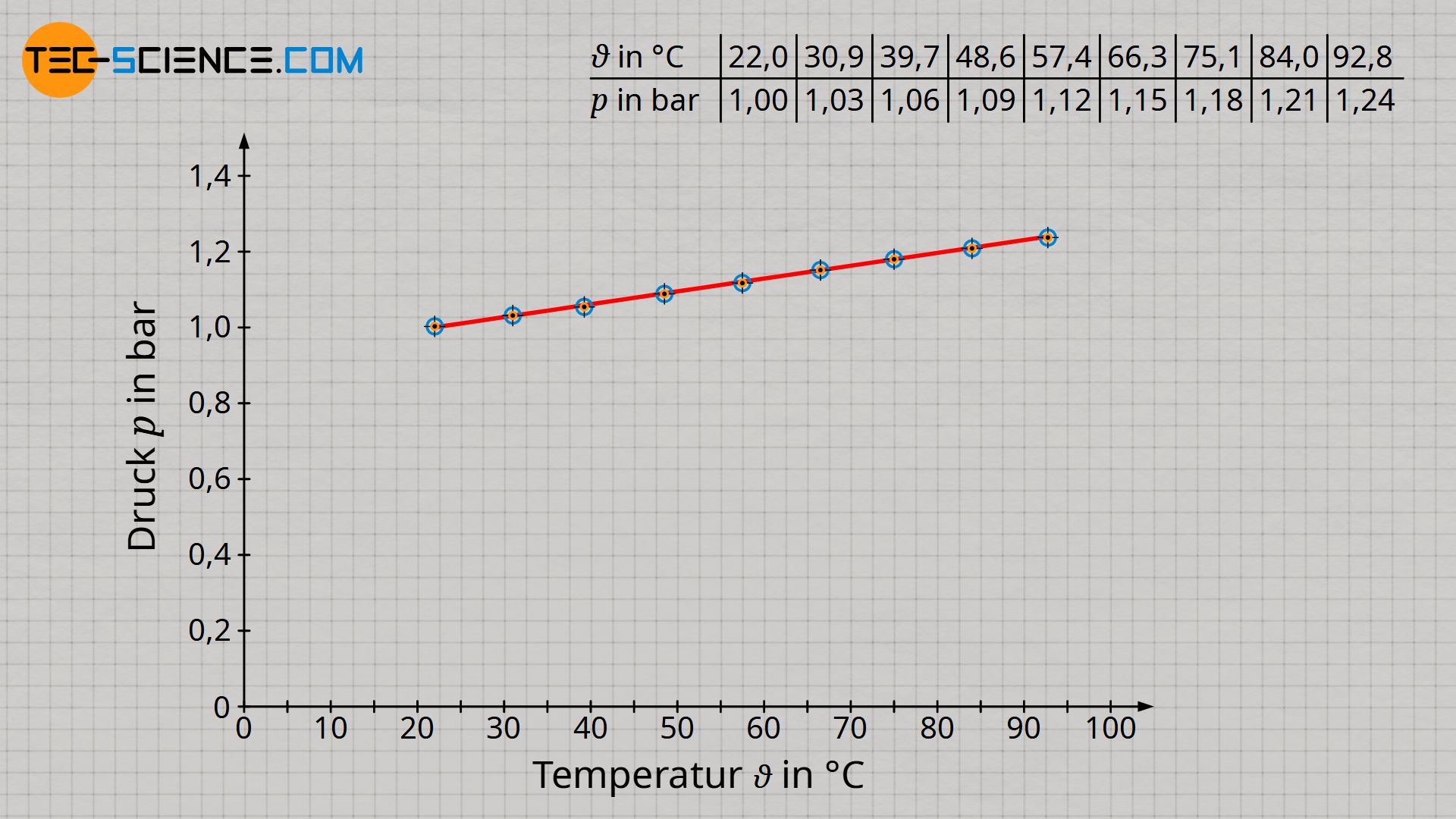
Aus dem Diagramm wird ersichtlich, dass der Druck linear mit der Temperatur ansteigt. Jedoch liegt in dieser Form noch keine Proportionalität zwischen beiden Größen vor! Proportionalität bedeutet, dass die Vervielfachung der einen Größe auch eine Vervielfachung der anderen Größe im selben Maße bewirkt. Eine Verdreifachung der Temperatur sollte demnach auch eine Verdreifachung des Drucks zur Folge haben. Dies ist im vorliegenden Fall allerdings nicht so! Zum Beispiel beträgt bei einer Temperatur von 22 °C beträgt der Druck 1 bar. Eine Verdreifachung der Temperatur auf 66 °C bewirkt jedoch nicht den dreifachen Druck von 3 bar, sondern nur ein Druck von 1,15 bar (15 %). Solange die Temperatur in der Einheit Grad Celsius angegeben wird, sind Druck und Temperatur also nicht proportional zueinander.
Proportionalität zwischen Druck und Temperatur (Einheit: Kelvin)
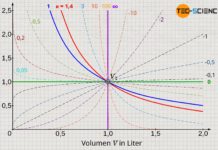
Tatsächlich verhalten sich Druck und Temperatur nur dann proportional zueinander, wenn die Temperatur in der Einheit Kelvin und nicht in Grad Celsius angegeben wird! Dies ist kein Zufall, denn auf Grundlage dieser Proportionalität wurde die Kelvinskala überhaupt erst eingeführt (siehe hierzu Artikel Temperaturskalen), da sich im Absoluten Nullpunkt keine Teilchenbewegung und somit auch kein Druck ergibt. Dieser Bewegungsnullpunkt wurde zum Referenzpunkt der Kelvinskala (0 K = -273 °C).
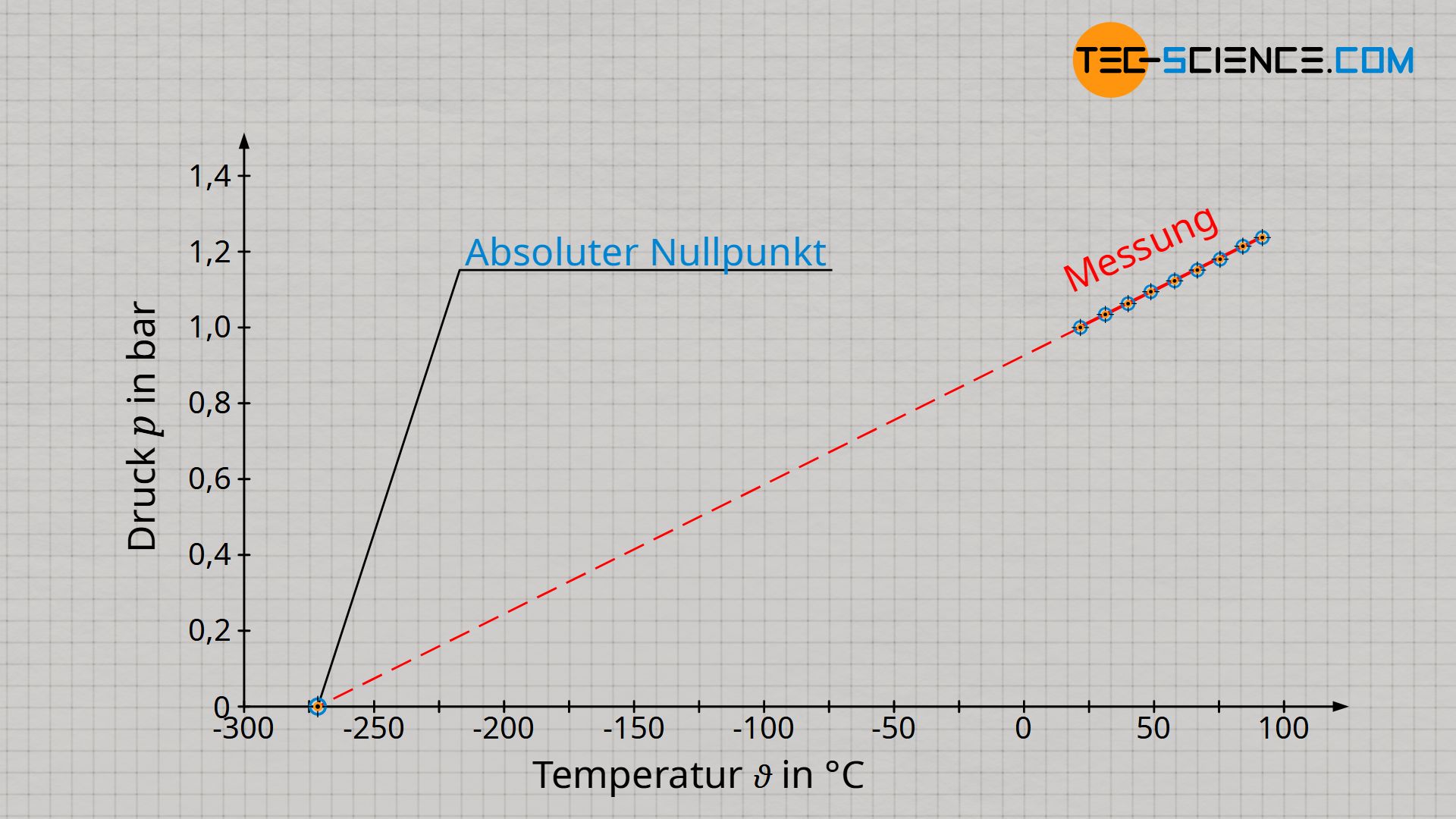
Wie kann man grundsätzlich eine Proportionalität zweier Größen in einem Diagramm von einer einfachen Linearität unterscheiden? Eine Proportionalität erkannt man in einem Diagramm immer daran, dass es sich nicht einfach nur um eine Gerade handelt, sondern insbesondere um eine Ursprungsgerade! Bei der Auftragung von Druck und Temperatur in der Einheit Kelvin, handelt es sich um eine solche Ursprungsgerade. Nur wenn man also die Temperatur in der Einheit Kelvin angibt, gilt ein proportionaler Zusammenhang zwischen Druck und Temperatur:
\begin{align}
&\boxed{p \sim T} ~~~~~\text{isochore Zustandsänderung eines geschlossenen Systems} \\[5px]
\end{align}
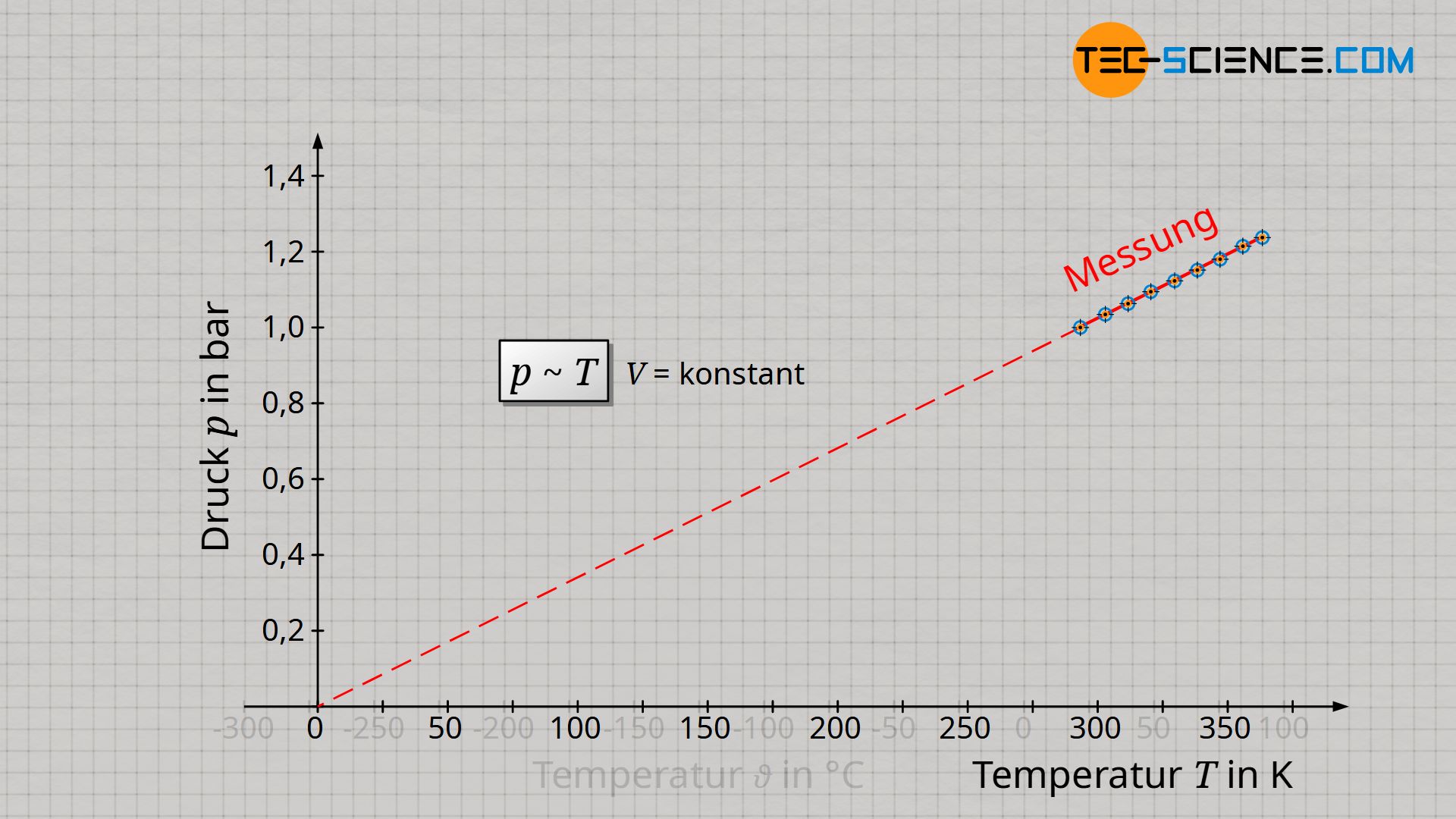
Folgerung
Wenn sich bei einem proportionalen Verhalten zweier Größen, die eine Größe im selben Maße verändert wie die andere Größe, dann ist der Quotient aus beiden Größe offenbar stets konstant. Dies Aussage kann auch anhand der Wertetabelle rasch verifiziert werden.
| Temperatur ϑ in °C | 22,0 | 30,9 | 39,7 | 48,6 | 57,4 | 66,3 | 75,1 | 84,0 | 92,8 |
| Temperatur T in K | 295,2 | 304,3 | 313,4 | 322,6 | 331,7 | 340,8 | 350,0 | 359,1 | 368,3 |
| Druck p in bar | 1,00 | 1,03 | 1,06 | 1,09 | 1,12 | 1,15 | 1,18 | 1,21 | 1,24 |
| p/T in 10-3 bar/K | 3,4 | 3,4 | 3,4 | 3,4 | 3,4 | 3,4 | 3,4 | 3,4 | 3,4 |
\begin{align}
&\boxed{ \frac{p}{T}= \text{konstant}}~~~~~ \text{Gesetz von Amontons} \\[5px]
\end{align}
Die Konstanz des Quotienten von Druck und Temperatur bei einem isochoren Prozess wurde unter anderem von dem Physiker Guillaume Amontons experimentell untersucht. Deshalb ist diese Gesetzmäßigkeit als Amontons’sches Gesetz bekannt (auch als 2. Gay-Lussac’sches Gesetz bezeichnet).
Das Gesetz von Amontons besagt, dass bei einer isochoren Zustandsänderung eines geschlossenen Systems, der Quotient von Druck und Temperatur konstant ist!
Verknüpfung zweier Zustände
Bei einem isochoren Prozess hat also der Quotient von Druck und Temperatur für alle Gaszustände denselben konstanten Wert. Deshalb gilt insbesondere, dass der Quotient von Druck und Temperatur in einem beliebigen (Anfangs-)Zustand 1 auch dem Quotienten von Druck und Temperatur in einem beliebigen (End-)Zustand 2 entspricht:
\begin{align}
&\frac{p_1}{T_1} =\text{konstant}= \frac{p_2}{T_2} \\[5px]
&\boxed{\frac{p_1}{T_1} = \frac{p_2}{T_2}} \\[5px]
\end{align}

Bei einer isochoren Zustandsänderung eines geschlossenen Systems, stehen zwei Zustände über den Quotienten von Druck und Temperatur in Zusammenhang!
Zusammenhang zum idealen Gasgesetz
Der oben gezeigte Zusammenhang zwischen zwei Gaszuständen ergibt sich auch aus dem idealen Gasgesetz für den Spezialfall einer Zustandsänderung bei konstantem Volumen (V1=V2):
\begin{align}
\require{cancel}
&\frac{p_1 \cdot \cancel{V_1}}{T_1} = \frac{p_2 \cdot \cancel{V_2}}{T_2} \\[5px]
&\boxed{\frac{p_1}{T_1} = \frac{p_2}{T_2}} \\[5px]
\end{align}
Die Konstanz des Quotienten aus Druck und Temperatur ergibt sich auch direkt anhand der thermischen Zustandsgleichung. Für den Fall, dass sich das Volumen nicht ändert (V=konstant) und das System geschlossen ist (m=konstant) gilt:
\begin{align}
&\boxed{p \cdot V = R_\text{s} \cdot m \cdot T} ~~~~~\text{thermische Zustandsgleichung}\\[5px]
&\frac{p}{T} = \underbrace{R_\text{s} \cdot \frac{m}{V}}_{=\text{konstant}} \\[5px]
&\underline{\frac{p}{T} =\text{konstant}} \\[5px]
\end{align}