Auftriebskräfte wirken nicht nur in Flüssigkeiten, sondern auch in Gasen. Am Beispiel eines Heißluftballons soll dies im Folgenden verdeutlicht werden.
Auftriebskraft
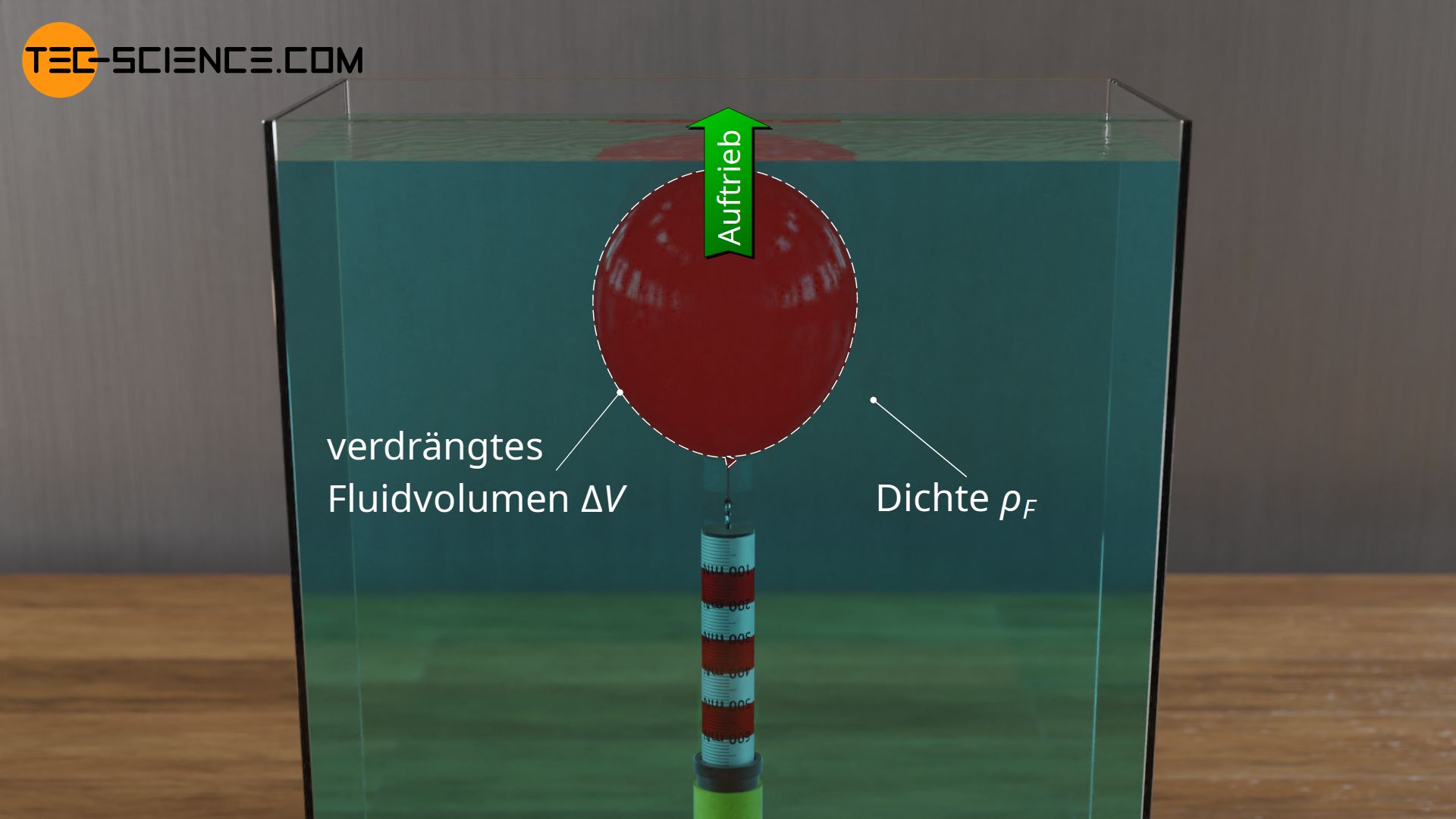
Im Artikel Auftrieb wurde auf die physikalische Ursache und das Zustandekommen der Auftriebskraft bereits im Detail eingegangen. Der Anschaulichkeit halber wurden dabei stets Flüssigkeiten betrachtet, in denen die Gegenstände jeweils eintauchten. Dabei zeigte sich, dass für den Betrag der Auftriebskraft zum einen das vom eingetauchten Gegenstand verdrängte Flüssigkeitsvolumen \(\Delta V\) und zum anderen die Dichte der Flüssigkeit \(\rho_F\) relevant ist (mit \(g\) als Fallbeschleunigung):
\begin{align}
&\boxed{F_A = \Delta V \cdot \rho_F \cdot g} ~~~~~\text{Auftriebskraft} \\[5px]
\end{align}
Aus dieser Gleichung wurde auch das archimedische Prinzip abgeleitet, das besagt, dass die Auftriebskraft eines Körpers gerade der Gewichtskraft der verdrängten Flüssigkeit. Hierzu kann in der oberen Gleichung zunächst das Produkt aus verdrängtem Flüssigkeitsvolumen und Flüssigkeitsdichte als verdrängte Flüssigkeitsmasse \(\Delta m\) interpretiert werden. Anschließend zeigt sich das Produkt aus Masse und Fallbeschleunigung als Gewichtskraft der verdrängten Flüssigkeit \(F_{G,ver}\):
\begin{align}
&F_A = \underbrace{\Delta V \cdot \rho_F}_{\Delta m} \cdot g \\[5px]
&F_A = \underbrace{\Delta m \cdot g}_{F_{G,ver}} \\[5px]
&\boxed{F_A = F_{G,ver}}~~~~~\text{Archimedisches Prinzip} \\[5px]
\end{align}
Von Flüssigkeiten zu Gasen
Grundsätzlich kann man sich nun auch eine Flüssigkeit vorstellen, deren Dichte man in Gedanken immer geringer und geringer werden lässt. Irgendwann wird man sich schließlich der Dichte von Gasen angenähert haben. Es gibt also keinen Grund, weshalb eine Auftriebskraft nicht auch in Gasen zustande kommen sollte. Und tatsächlich zeigt die Praxis, dass in Gasen ebenfalls Auftriebskräfte wirken. Diese werden mit denselben Gesetzmäßigkeiten berechnet wie sie auch für Flüssigkeiten gelten. Die Dichte \(\rho_F\) steht deshalb im Allgemeinen für die Dichte des umgebenden Fluides (egal ob Flüssigkeit oder Gas).
Die Berechnung der Auftriebskraft in Gasen ist im Vergleich zu Flüssigkeiten meist insofern einfacher als dass ein Körper in der Regel stets vollständig in das Gas eintaucht. Das verdrängte Gasvolumen entspricht somit dem Körpervolumen. Bei Flüssigkeiten muss hingegen beachtet werden, dass diese auch nur teilweise in die Flüssigkeit eintauchen können. Das verdrängte Flüssigkeitsvolumen entspricht dann nur dem tatsächlich eingetauchten Körpervolumen.
Da Gase im Vergleich zu Flüssigkeiten relativ geringe Dichten aufweisen, ist die verdrängte Gasmasse in die ein massiver Festkörper eintaucht im Vergleich zu seiner eigenen Masse häufig vernachlässigbar klein. Die Auftriebskraft kann in einem solchen Fall dann gegenüber der Gewichtskraft des Körpers meist vernachlässigt werden. Eine Person verdrängt bspw. durch sein eigenes Körpervolumen rund 80 Liter Luft. Bei einer Luftdichte von ca. 1,25 g pro Liter, beträgt die verdrängte Luftmasse somit 100 g. Eine 80 kg schwere Person wird durch die Auftriebskraft der umgebenden Luft somit scheinbar um 100 g leichter (dies entspricht nur rund 0,1 % des Körpergewichtes).
In Fällen wo das Gewicht eines Körpers im Vergleich zu seinem Volumen jedoch relativ klein ist, spielt die Auftriebskraft jedoch auch in Gasen jedoch eine große Rolle. Dies wird vor allem dann der Fall sein, wenn man zwei gasförmige Stoffe betrachtet. Mit Helium gefüllte Ballons in Luft sind hierfür ein typisches Alltagsbeispiel, bei dem die wirkende Auftriebskraft für das Aufsteigen des Ballons sorgt.

Das Helium ist in diesem Fall leichter als die verdrängte Luftmasse, sodass die gemäß des archimedischen Prinzips entstehende Auftriebskraft größer ist als die Gewichtskraft des Heliums. Diese Auftriebskraft ist so groß, dass sie nicht nur das Helium sondern auch noch die Masse des Ballons in die Luft hebt (plus evtl. Gewicht der Befestigungsschnur). Mit der Zeit wird das Helium jedoch aus dem Ballon entweichen und dieser schrumpfen, sodass irgendwann die Auftriebskraft nur noch dafür ausreicht den Ballon in der Schwebe zu halten. In diesem Fall entspricht die Auftriebskraft gerade der Gewichtskraft Heliums plus die des Ballons. Sollte noch mehr Helium entweichen, dann wird das Volumen des Ballons irgendwann so klein sein, dass deutlich weniger Luftmasse verdrängt wird. Die Auftriebskraft sink gemäß des archimedischen Prinzips. Schließlich kann die Auftriebskraft die Gewichtskraft des Heliums und die des Ballons nicht mehr kompensieren und der Ballon sinkt zu Boden.
Heißluftballon
Dasselbe Prinzip des Auftriebs nutzen auch Heißluftballons. Anstelle von Helium wird einfach erwärmte Luft genutzt. Ein Heißluftballon besteht aus einer luftdichten Ballonhülle, die sich aus mehreren, miteinander vernähten Segmenten zusammensetzt. Am unteren Ende des Ballons ist der Korb mit Tragseilen befestigt. Auf einem Rahmen sind die Brenner angebracht, die von Gasflaschen gespeist werden.

Typische Daten eines Heißluftballons sind in der unteren Abbildung gegeben, aus denen anschaulich die Funktionsweise hervorgeht. Die Hülle des Ballons besitzt dabei in etwa ein Volumen von 4000 m³. Dies bedeutet, dass der Ballon somit ein Volumen von 4000 m³ kalter Umgebungsluft verdrängt. Bei einer Umgebungstemperatur von rund 24 °C hat die Luft eine Dichte von ca. 1,17 kg/m³. Mit einem Volumen von 4000 m³ verdrängt der Ballon somit eine kalte Luftmasse von rund 4700 kg. Gemäß des archimedischen Prinzips führt dies entsprechend zu einer Auftriebskraft von 47 kN. Wäre im Ballon nun dieselbe Luft wie außerhalb, dann befände sich in der Ballonhülle logischerweise eine Luftmasse von 4700 kg. Die Auftriebskraft der Luft entspräche dann der Gewichtskraft und die Luft würde praktisch im Ballon schweben, aber keine effektive, aufwärts gerichtete Kraft erzeugen.

Deshalb wird die Luft im Inneren des Ballons mit einem Gasbrenner auf teilweise über 100 °C erwärmt. Als Folge hiervon sinkt die Luftdichte und mit ihr die Luftmasse im Ballon. Anschaulich lässt sich die Abnahme der Luftmasse im Ballon damit erklären, dass sich die erwärmte Luft ausdehnt und dabei teilweise aus dem Ballon ausströmt. Anders als ein gewöhnlicher Luftballon oder Heliumballon ist ein Heißluftballon nämlich kein geschlossenes System, sondern nach unten hin offen, wo der Gasbrenner die Luft erwärmt (und auch nach oben hin offen, später mehr dazu). Beachte, dass sich das Volumen des Ballons während der Erwärmung praktisch nicht ändert, sodass sich an der verdrängten Luftmasse bzw. der damit verbundenen Auftriebskraft ebenfalls nichts ändert.
Bei einer Innentemperatur der Luft von bspw. 104 °C, ist die Dichte auf etwa 0,92 kg/m³ gesunken, sodass sich im 4000 m³ großen Ballonvolumen dann nur noch eine Luftmasse von ca. 3700 kg befindet. Der Auftriebskraft von 47 kN steht nun also nur noch eine Gewichtskraft von 37 kN entgegen. Somit erzeugt die erwärmte Luft eine aufwärts gerichtete Kraft von 10 kN. Dies ist ausreichend um eine Gesamtmasse von insgesamt 1000 kg anzuheben! Eingerechnet werden muss dabei die Ballonhülle mit etwa 150 kg und der Brenner sowie die Gasflaschen mit insgesamt 250 kg. Abzüglich einer Korbmasse von 100 kg verbleiben somit noch 500 kg zur Beförderung der Personen.
Da die Auftriebskraft eines Heißluftballons durch die verdrängte Luftmasse (d.h. durch das Ballonvolumen) festgelegt ist und während der Fahrt praktisch nicht verändert werden kann, muss zum gezielten Absenken des Ballons die Luftmasse im Ballon wieder erhöht werden. Dies wird durch ein Loch an der Oberseite des Ballons erreicht, das beim Aufsteigen verschlossen ist und zum Absenken mit einem Seil gezielt geöffnet werden kann. Die heiße, leichte Luft kann hierdurch nach oben entweichen und kalte, schwere Luft von unten nachströmen. Die Luftmasse im Ballon erhöht sich wieder und die Gewichtskraft wird größer als die Auftriebskraft, sodass der Heißluftballon nun nach unten sinkt.
Ausblick
Im Artikel Auftrieb wurde das Zustandekommen der Auftriebskraft in Flüssigkeiten durch die unterschiedlichen hydrostatischen Drücke an der Unterseite bzw. Oberseite des eingetauchten Gegenstandes erklärt. Dass nun auch in Gasen Auftriebskräfte wirken, legt folglich den Schluss nahe, dass es auch in Gase so etwas wie „hydrostatische“ Drücke gegeben muss. Auf die analoge Weise wie der Druck in Flüssigkeiten mit zunehmender Tiefe zunimmt, sollte also auch der Druck in Gasen mit zunehmender Tiefe zunehmen bzw. mit zunehmender Höhe abnehmen. Und tatsächlich ist auch dies genau der Grund dafür, weshalb der atmosphärische Luftdruck mit zunehmender Höhe – zum Beispiel auf Bergen – abnimmt. Mehr Informationen hierzu im Artikel Barometrische Höhenformel.






