In homogeneous nucleation, nuclei consisting of the same substance as the melt trigger solidification.
Gibbs energy
In order to understand the processes of nucleation, an energetic analysis is indispensable. In this context the so-called Gibbs energy plays a central role. Gibbs energy is often referred to as Gibbs free energy, Gibbs function or free enthalpy.
The Gibbs energy balances the enthalpy \(H\) (and with it the internal energy \(U\) as well as pressure \(p\) and volume \(V\)) and the entropy \(S\) at a given temperature \(T\) of a substance:
\begin{equation}
\label{gibbs_energie}
\boxed{G=H – T \cdot S } ~~~ \text{bzw.} ~~~ \boxed{G= U + pV – S \cdot T}
\end{equation}
The Gibbs energy is the decisive measure of whether a chemical or thermodynamic reaction at constant temperature and constant pressure (which is usually the case in a solidification process!) takes place voluntarily with the release of energy or must be forced with the supply of energy.
If the Gibbs energy increases during a reaction (\(\Delta G>0\)), this requires a external energy input (endergonic reaction). The energetically higher final state means that the reaction does not take place voluntarily.
However, if the Gibbs energy decreases with a reaction (\(\Delta G<0\)), then the reaction will take place voluntarily with a release of energy. The energetically more favourable state will occur accordingly (exergonic reaction).
If the Gibbs energy does not change during a reaction (\(\Delta G=0\)), then the reaction will take place to the same extent in one direction as in the other (thermodynamic equilibrium).
The direction of thermodynamic processes can be assessed on the basis of the Gibbs energy:
\begin{align}
\label{unfreiwillig}
&\Delta G > 0 \text{ : Reaction is not voluntary!} \\[5px]
\label{freiwillig}
&\Delta G < 0 \text{ : Reaction is voluntary!} \\[5px]
&\Delta G = 0 \text{ : Reaction takes place to the same extent in both directions!} \\[5px]
\notag \\[5px]
\end{align}
Gibbs energy of different states of matter
The figure below shows the schematic curve of Gibbs energy as a function of the temperature for the solid, liquid and gaseous states of a substance.
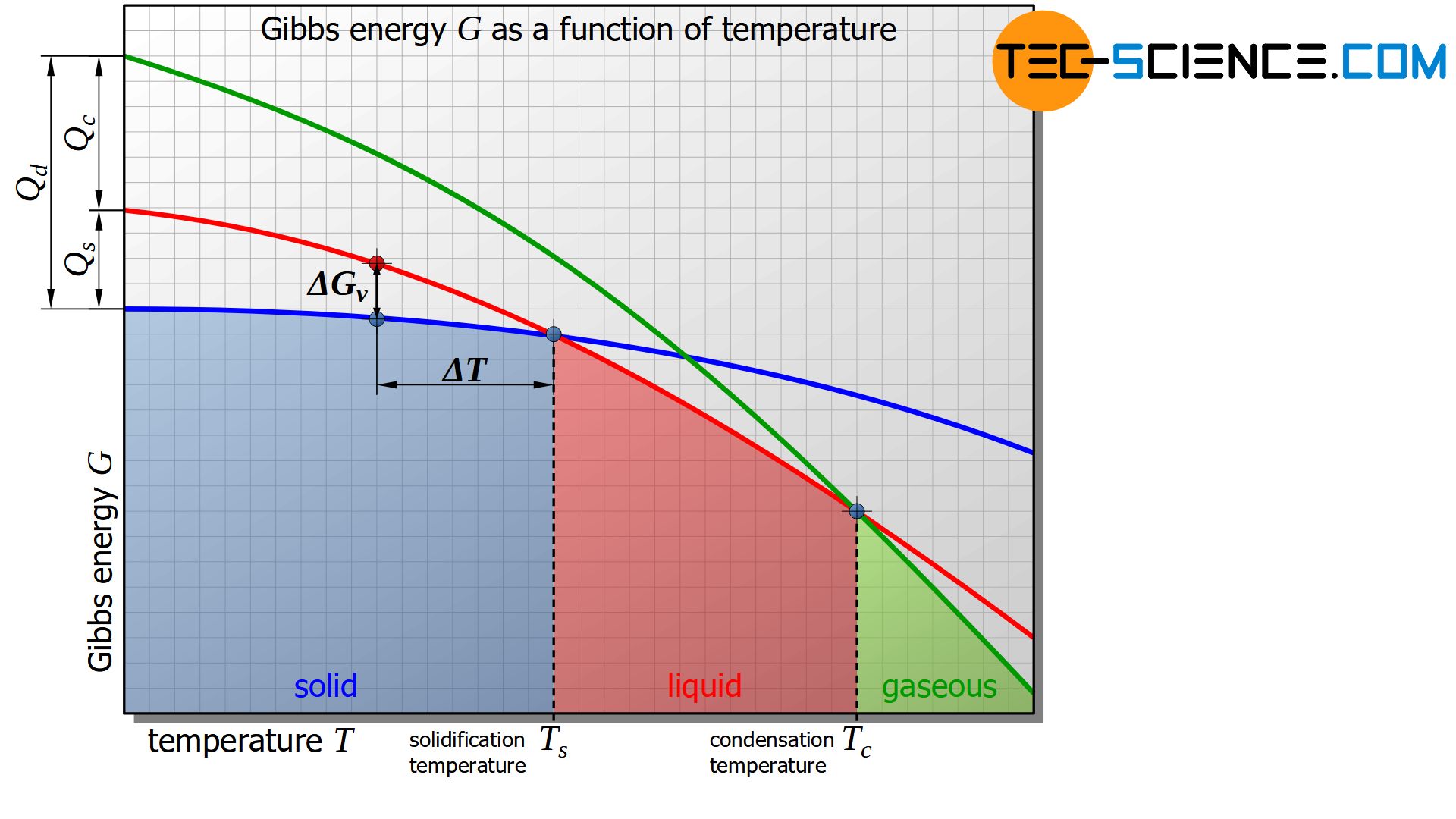
It is shown that below a certain temperature the Gibbs energy of the solid state is energetically more favourable than that of the liquid state. This intersection of the corresponding Gibbs curves indicates the solidification temperature or, conversely, the melting temperature of the material. At the solidification point, the Gibbs energy of the liquid and solid states is obviously equal.
In the analogous way, the evaporation or condensation temperature can be defined as the intersection of the Gibbs curves between the liquid and the gaseous state.
Basically, only the state of matter with the lowest Gibbs energy is in a thermodynamic equilibrium. If the temperature falls below the solidification point, the liquid state is no longer in thermodynamic equilibrium due to the higher Gibbs energy.
Rather, at this point there is a reduction in Gibbs energy at the transition from the solid to the liquid phase (\(\Delta G<0\)). In accordance with the above-mentioned law, phase transformation from liquid to solid state takes place voluntarily [see equation (\ref{freiwillig})]. So a thermodynamic system always voluntarily assumes the state of lowest Gibbs energy.
At a certain temperature, only the state of matter with the lowest Gibbs energy is thermodynamically stable (thermodynamic equilibrium)!
The difference between the Gibbs energies of two states is thus the driving force for a substances to change their state of matter when falling below or exceeding a certain temperature and thus take up the state of lowest possible Gibbs energy.
The difference in Gibbs energy is the driving force for a change of state!
This circumstance already expresses the fact that simply reaching the solidification temperature is not sufficient to cause a liquid substance to solidify. This is because a drive is only given when there is a difference in Gibbs energy and thus a fall below the solidification temperature (undercooling!).
Latent heat
The difference in Gibbs energies between the solid and liquid states of a substance at absolute zero corresponds to the heat of solidification\(Q_s\) or enthalpy of solidification of the substance.
In the same way, the condensation heat \(Q_c\) or enthalpy of condensation can be determined in the difference of the Gibbs energy between the liquid and the gaseous state at absolute zero.
The sum of both enthalpies then corresponds to the heat of desublimation \(Q_d\) or enthalpy of desublimation.
Activation energy
Even if subcooling results in principle in a drive for phase transformation (\(\Delta G_v\)), this process does not yet run automatically. An important factor that also influences the Gibbs energy of a solidifying nucleus has not yet been taken into account.
The situation can be compared to a standing car on a hill, which has just passed the highest point. Although the car is basically ready to roll down the hill on its own towards the state of equilibrium, the last energy needed to overcome the static friction and get the rolling started is missing.
In the analogous way, even after the temperature has fallen below the solidification point a “resistance” must first be overcome before the solidification can actually take place on its own. This “resistance” is mainly the surface energy to be applied, which is necessary to form the solid surface during crystallization. Even if the forming particle is to grow, surface energy must be used so that the crystal can increase its surface area. Such an energy input to trigger a process is generally referred to as activation energy.
The surface energy can be understood as resistance against phase transformation (activation energy)!
Note that the Gibbs curves shown in the upper section refer only to the energetic conditions in liquid and solid state. This does not take into account energy sales that are necessary for the “initiation” of the conversion processes, such as surface energy.
Gibbs energy of a nucleus
The change in Gibbs energy \(\Delta G_{n}\) of a considered nucleus which is currently solidifying when the solidification temperature \(T_s\) is reached can ultimately be traced back to two essential terms, which are discussed in more detail in the following sections:
\begin{align}
\label{unterkuehlung}
&\boxed{\Delta G_n = \Delta G_v + \Delta G_s} \\[5px]
&\Delta G_v<0 \text{ für } T<T_s\\
&\Delta G_v>0 \text{ für } T>T_s\\
&\Delta G_s>0\\
\end{align}
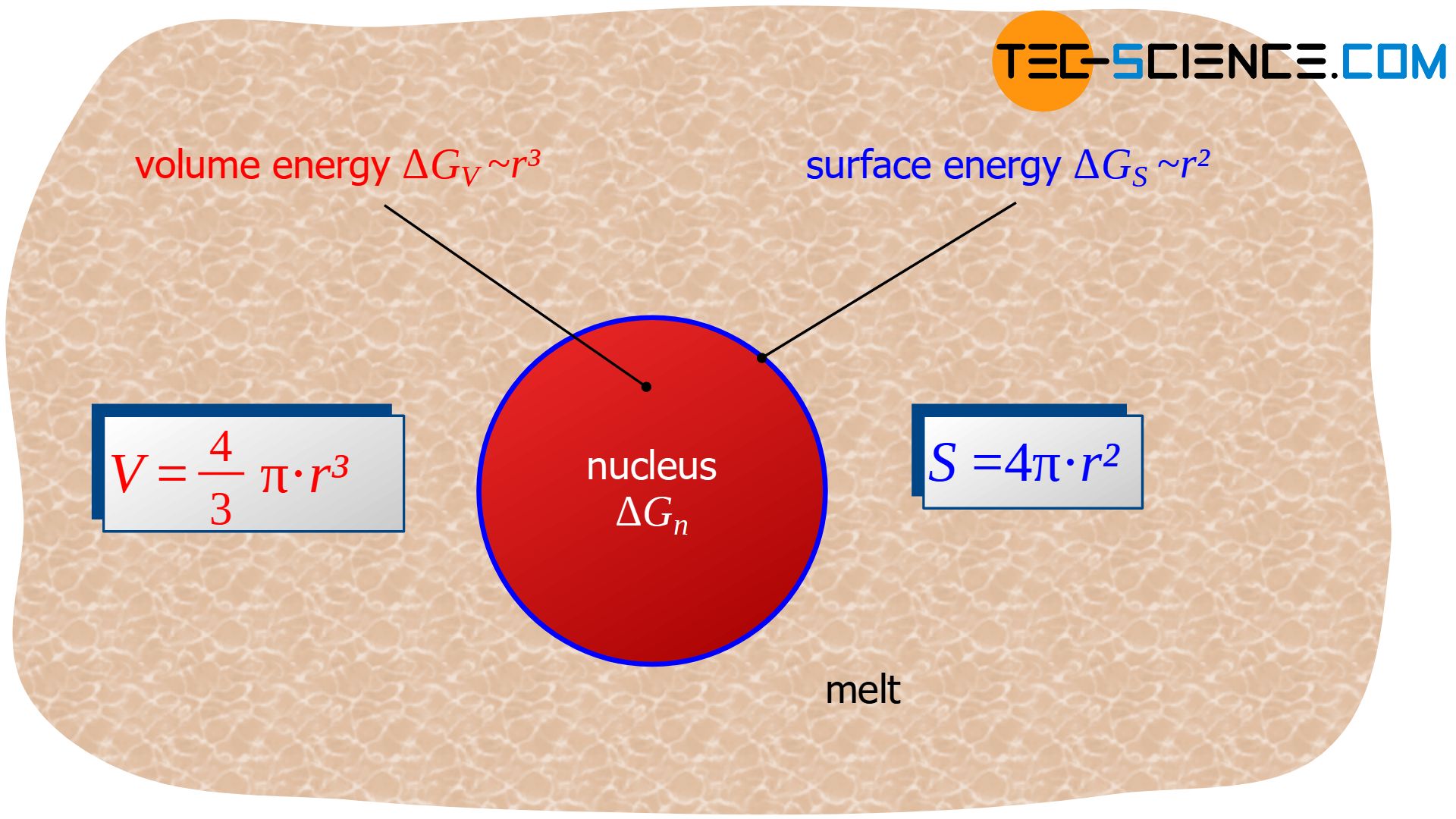
Note: Deformation energies can be neglected when transforming from a liquid state to a solid state. Only phase transformations within in the solid state require deformation energy. In such a case a third (positive) term which considers these effects will be present in equation (\ref{unterkuehlung}).
Volume energy
The first term \(\Delta G_{v}\) in equation (\ref{unterkuehlung}) results on the basis of lower Gibbs-energy of a solid state in comparison with a liquid state. As long as the temperature is below the solidification temperature, this energy contribution is always negative (\(\Delta G_{v}<0\)). After all, the solid state below the solidification temperature has a lower Gibbs energy than the liquid state.
Put simply, this means nothing else than that the solidified volume below the solidification temperature has a “volume energy” lower by the amount \(\Delta G_{v}\) than in the liquid state.
This term would only be positive if it were assumed that a solid nucleus is formed above the solidification temperature due to statistical fluctuations, because above the solidification point, the solid state has a higher Gibbs energy than the liquid phase (more about this later).
For the term \(\Delta G_{v}\) the solidifying volume is decisive, i.e. the volume of the (short-term solidified) nucleus that is formed. If a spherical nucleus with radius \(r\) is assumed, the reduction of Gibbs energy \(\Delta G_{v}\) is proportional to the spherical volume \( V=\frac{4}{3} \pi r^3 \):
\begin{align}
\label{volumenenergie1}
&\Delta G_v = -\underbrace{\frac{4}{3} \pi r^3 \cdot \rho}_{\text{nucleus mass}} \cdot \Delta g_v \\[5px]
\label{volumen}
& \Delta G_v \sim r^3 \\[5px]
\end{align}
In equation (\ref{volumenenergie1}) the term \(\Delta g_v\) denotes the specific Gibbs energy change (“Gibbs energy per solidified mass”), which is obviously dependent on the untercooling \(\Delta T\) of the nucleus. With given supercooling the term \(\Delta G_{v}\) is thus proportional to the third power of the considered nucleus radius.
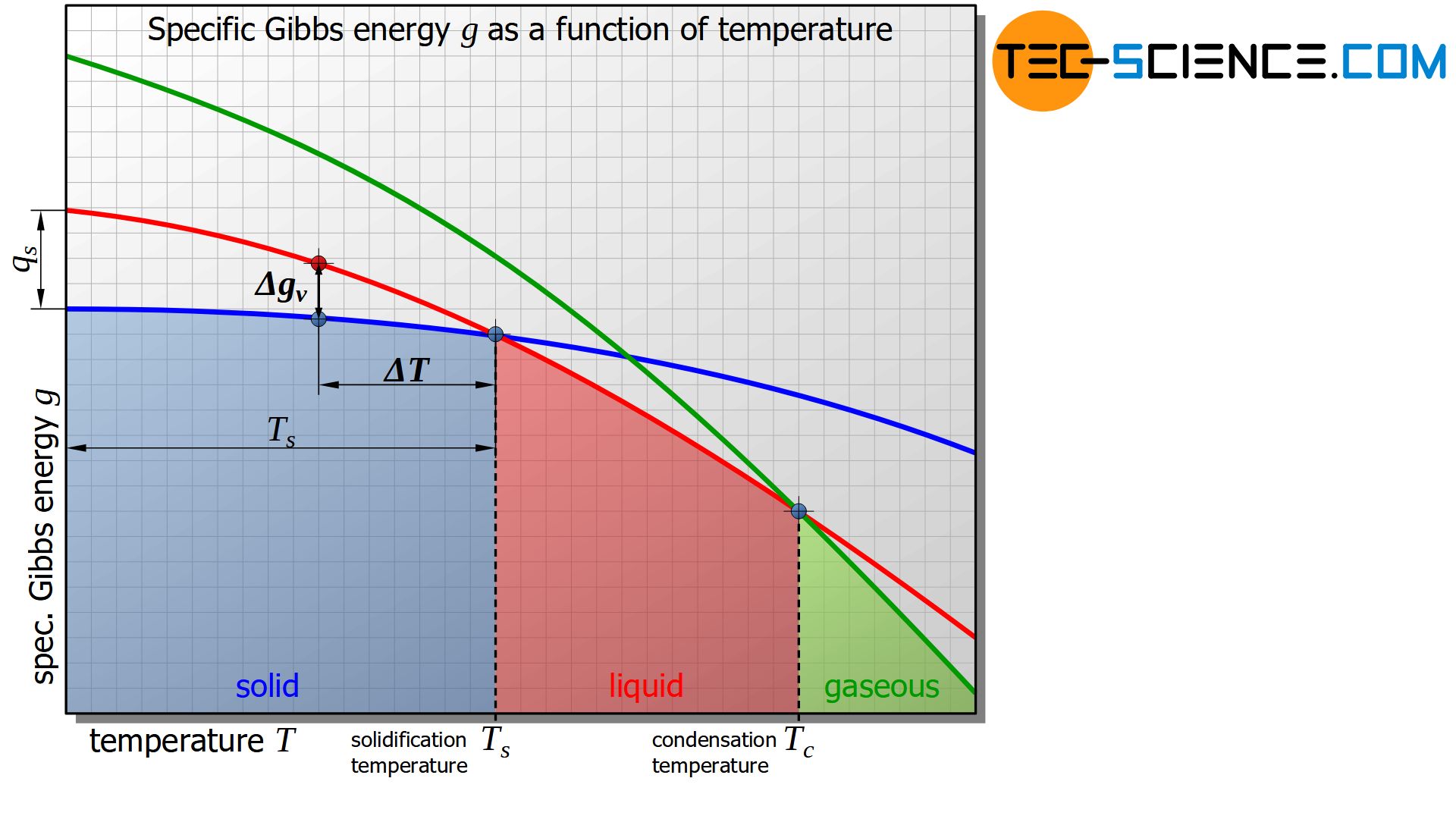
The change in specific Gibbs energy \(\Delta g_v\) can be approximately assumed to be proportional to the undercooling \(\Delta T\), if it is related to the solidification temperature \(T_s\). The proportionality factor corresponds precisely to the specific heat of solidification \(q_s\). This consideration is obtained by using the intercept theorem (the error due to the curved lines instead of straight lines can often be neglected in practice):
\begin{align}
&\frac{\Delta g_v}{\Delta T} \approx \frac{q_s}{T_s} \\[5px]
\label{schmelzwaerme}
&\boxed{\Delta g_v \approx q_s \cdot \frac{\Delta T}{T_s}} \\[5px]
\end{align}
If equation (\ref{schmelzwaerme}) is combined with equation (\ref{volumenenergie1}), the change in Gibbs energy of the solidified nucleus is dependent on the nucleus radius \(r\) and undercooling \(\Delta T\):
\begin{align}
\label{volumenenergie}
\boxed{\Delta G_v = -\frac{4 \pi \rho ~ q_s}{3 ~ T_s} \cdot \Delta T \cdot r^3} ~~~~~\text{(decrease of “volume energy”)} \\[5px]
\end{align}
The undercooling of metals during homogeneous nucleation is in the order of about 25 % of the solidification temperature. For iron with a solidification temperature of \(T_s=1810 \text{ K}\) this means, for example, a undercooling of \(\Delta T = 450 \text{ K}\).
Surface energy
The second term \(\Delta G_{s}\) in equation (\ref{unterkuehlung}) refers to the surface energy \(\Delta G_s\) which must be considered at occurrence of the solidified nucleus. This part causes the Gibbs energy to increase with the use of energy. The term \(\Delta G_s\) is therefore always positive, regardless of whether the nucleus itself forms above or below the solidification temperature due to thermal fluctuations in the melt (\(\Delta G_s>0\)).
The surface energy is obviously proportional to the surface of the spherical nucleus \( S = 4 \pi r^2 \) and thus proportional to the square of the nucleus radius \(r\):
\begin{align}
\label{a}
&\boxed{\Delta G_s = 4 \pi r^2 \cdot \gamma} ~~~~~~\text{(“surface energy” to be applied)} \\[5px]
\label{oberflaeche}
& \Delta G_s \sim r^2 \\[5px]
\end{align}
In equation (\ref{a}) the term \(\gamma\) denotes the specific surface energy (also called surface tension). Overall, the change in Gibbs energy of a nucleus assumed to be spherical with the radius \(r\) at a given undercooling \(\Delta T\) can be calculated as follows:
\begin{align}
\label{keim}
&\boxed{\Delta G_n(r, \Delta T) = -\frac{4 \pi \rho ~ q_s}{3 ~ T_S} \cdot \Delta T \cdot r^3 + 4 \pi ~ \gamma \cdot r^2} \\[5px]
\end{align}
This equation is interpreted in more detail in the following section.
Critical nucleus radius
For temperatures above the solidification temperature the undercooling is mathematically considered negative (\(\Delta T<0\)) and thus both terms in equation (\ref{keim}) positive. In this case, the figure below shows the change in Gibbs energy \(\Delta G_{n}\) with increasing nucleus radius \(r\).
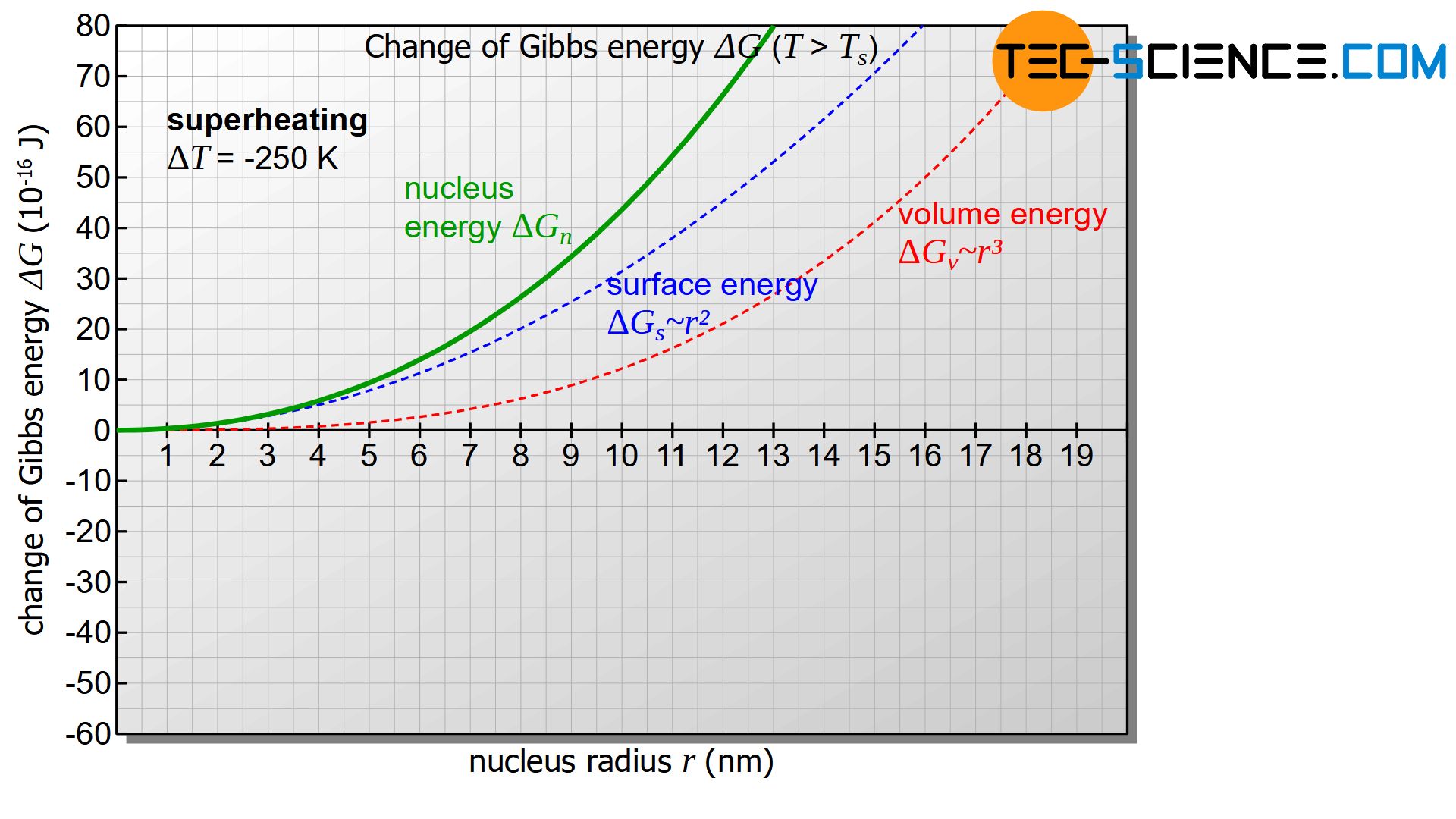
In all cases the Gibbs energy of the nucleus \(\Delta G_{n}\) will increase (positive change of Gibbs energy). As a result, there will be no thermodynamic equilibrium between the solidified nucleus and the remaining melt. It may well be that a nucleus forms, but due to the unstable state, it will quickly dissolve by releasing energy and strives for a minimum of Gibbs’ energy.
Above the solidification temperature, a formed nucleus will dissolve immediately with release of energy!
However, the diagram only becomes interesting when the temperature of the melt or the nucleus is below the solidification temperature and thus there is a positive undercooling (\(\Delta T>0\)). In this case the first term in equation (\ref{keim}) becomes negative. The diagram below shows the course of Gibbs energy change \(\Delta G_{n}\) of the nucleus as a function of its radius. The diagram now shows a maximum in the change of Gibbs energy (green dot in the figure). This curve will be interpreted in more detail below.
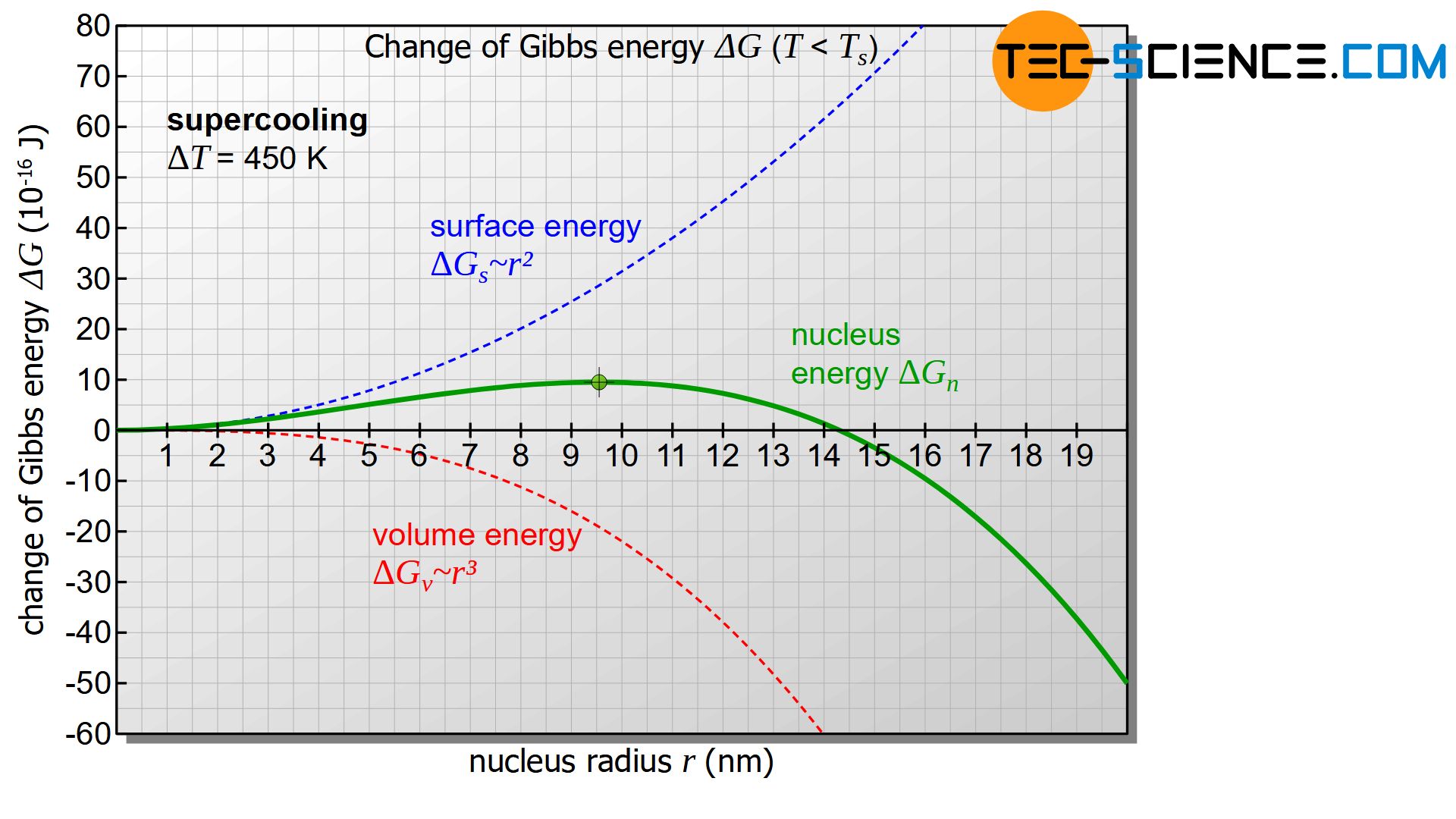
First, it is assumed that a solid nucleus with the radius \(r_1\) is formed, which is to the left of the maximum of the Gibbs curve (see figure below). To form such a nucleus, the Gibbs energy obviously needs to be increased. This is done by statistical fluctuations in the thermal energy of the melt, which can provide this amount of energy in the short term.
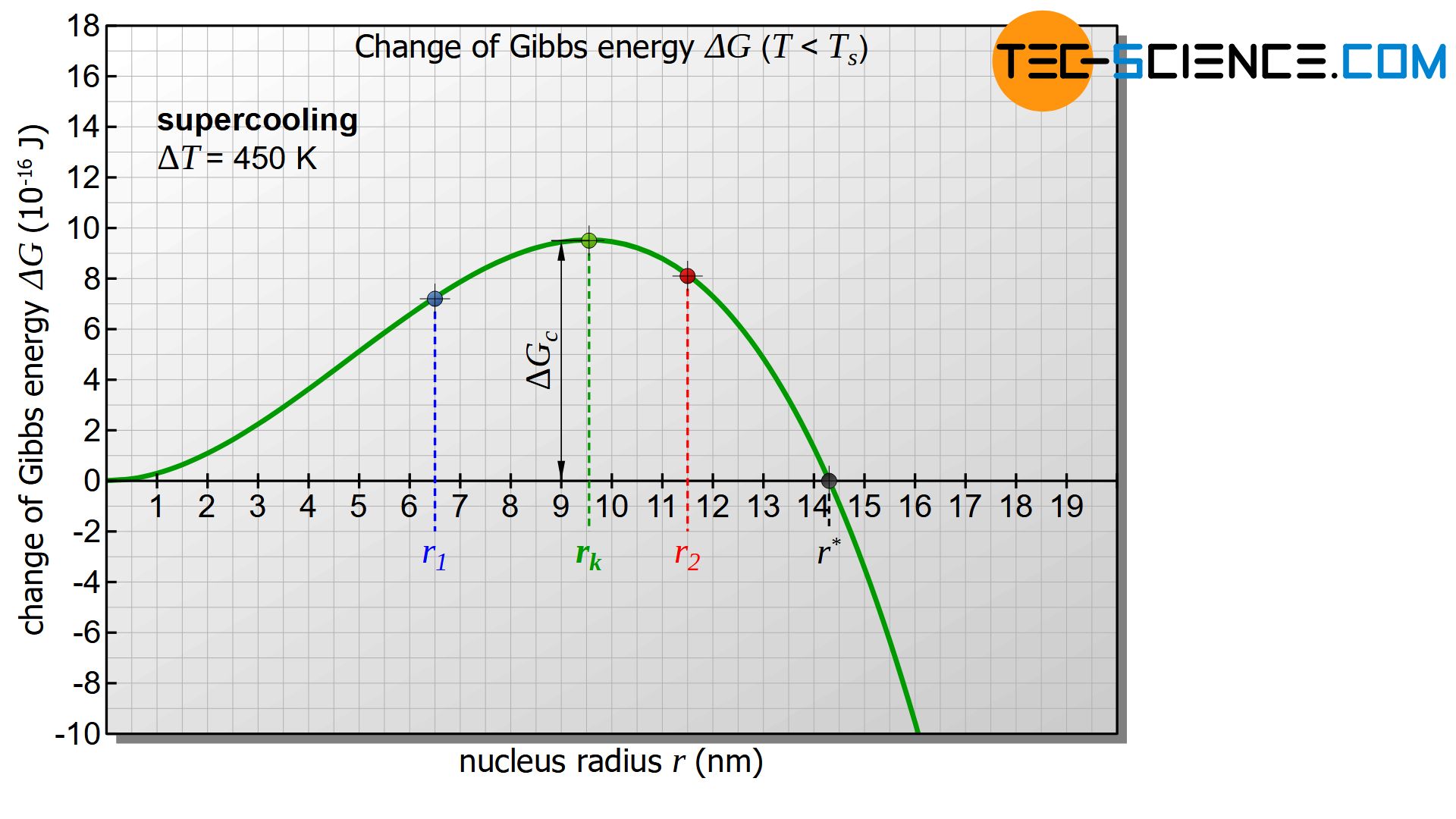
If the nucleus is then to continue to grow and thus initiate the solidification process, the nucleus must obviously become larger. According to the diagram, however, an increase in the radius is only possible with a further increase in Gibbs energy. Such an increase in Gibbs energy is not voluntary! Rather, the reduction of Gibbs energy and thus the reduction of the nucleus occurs voluntarily and is therefore more likely. The result is that the randomly formed nucleus dissolves again with a release of energy.
Now a randomly formed nucleus with the radius \(r_2\) is considered, which is to the right of the maximum of the Gibbs energy curve. This formation also occurs through thermal fluctuations in the melt, which causes the corresponding increase in Gibbs energy in the short term.
In such a case, according to the diagram, a reduction of the nucleus radius is only possible with the use of energy (increase of Gibbs energy) and will therefore not take place voluntarily. The nucleus will not dissolve on its own! Rather, the solidified germ will now voluntarily increase its radius while reducing Gibbs energy. Of course, this can only be done by adding further particles from the melt. Thus the beginning of the voluntary nucleus growth is given and the solidification process is initiated!
Only nucleus of a certain size are capable of growth and can initiate the solidification process!
This critical nucleus radius \(r_c\) results from the maximum of the Gibbs function, which can be obtained by derivation:
\begin{align}
\label{maximum}
&\frac{d (\Delta G_n)}{dr} = 0 \\[5px]
& -\frac{4 \pi \rho ~ q_s}{T_s} \cdot \Delta T \cdot r^2 + 8 \pi \gamma \cdot r = 0 \\[5px]
& \frac{4 \pi \rho ~ q_s}{T_s} \cdot \Delta T \cdot r = 8 \pi \gamma \\[5px]
\label{kritisch}
& \boxed{r_c = \frac{2 \gamma ~ T_s}{q_s~ \rho ~\Delta T}}
\end{align}
Typical values for the surface tensions of technically relevant metals are in the range between 1 and 4 J/m². If a value of \(\gamma\) = 2.5 J/m² and a solidification temperature of \(T_s = 1810 K\) is assumed for iron and a specific solidification heat of 268 kJ/kg and a density of \(\rho\) = 7870 kg/m³ is considered, then a undercooling of \(\Delta T = 450 K\) results in a critical nucleus radius \(r_c\) of approximately 9.5 nm. Approximately 300,000 atoms are then required to form such a nucleus.
Free energy barrier for nucleation
As can be seen from the diagram above for the change in Gibbs energy, energy must be used to produce the nucleus in order to increase Gibbs energy accordingly. This is achieved by thermal fluctuations in the melt, which can supply this amount of energy at local level in the short term. This amount of energy to be overcome is also called free energy barrier (activation energy for nucleation).
The amount of energy that has to be supplied for a stable formation of a nucleus is called free energy barrier (activation energy for nucleation)!
Only under the assumption that a randomly formed nucleus has a radius greater than \(r^*\) does crystallization take place directly with energy output. However, due to the large number of atoms required for this, the probability that such a large nucleus will form is low.
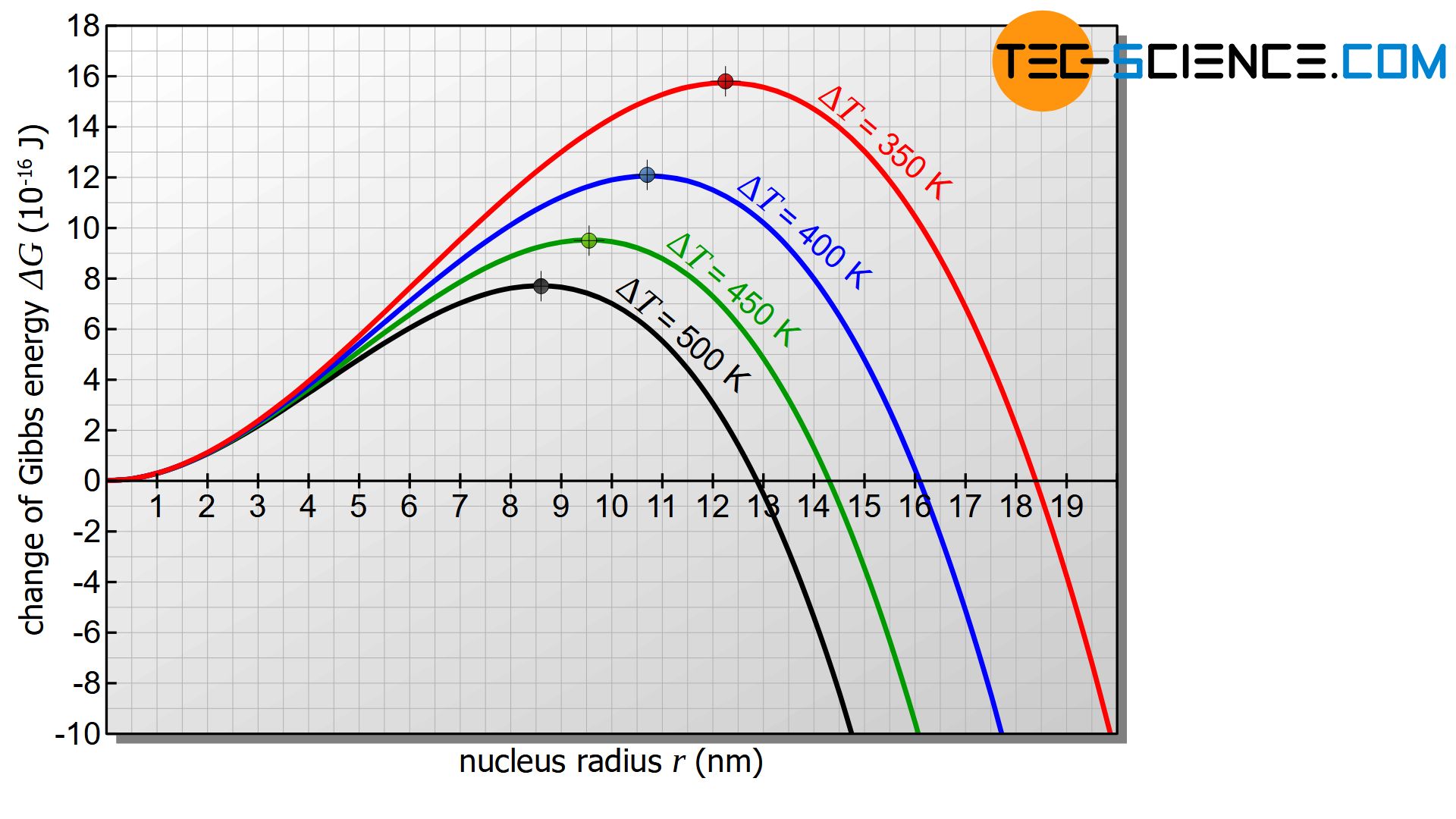
Undercooling \(\Delta T\) has obviously decisive influence on the critical radius according to the equation (\ref{kritisch}). The greater the supercooling \(\Delta T\) the smaller the critical radius. At the same time, the free energy barrier decreases as the critical radius decreases. As undercooling progresses, it becomes increasingly likely that nuclei capable of growth will form. Many nuclei can then form, which leads to a fine-grained structure. However, this only applies as long as the supercooling is not too great (more on this later).
Within certain limits a large supercooling leads to increased nucleation!
The free energy barrier \(\Delta G_c\) can be determined by inserting equation (\ref{kritisch}) into equation (\ref{keim}), so that the direct relationship to undercooling \(\Delta T\) becomes apparent:
\begin{align}
&\boxed{\Delta G_c = \frac{16 ~\pi ~ \gamma^3 ~ T_S^2}{3 ~ q_s^2 ~ \rho^2 ~ \Delta T^2} } \\[5px]
\end{align}
For the numerical example above, the energy barrier is in the order of about \(9.5 \cdot 10^{-16} \text{J}\).
Note that both the activation energy for nucleation and the critical nucleus radius increase with low undercooling and even become infinitely large when the solidification temperature is reached. A stable nucleation is therefore no longer possible when the solidification point is reached!
Nucleation rate
In the previous section it was shown that the critical nucleus radius and the energy barrier decrease with progressive undercooling. The latter is applied by thermal fluctuations of the melt, whereby several smaller fluctuations are more likely than single large fluctuations. This explains why the number of growth-capable nuclei increases with progressive undercooling. A strong supercooling is therefore usually desired, as this leads to a fine-grained and thus solid and tough microstructure.
However, there are also limits to the increasing number of nuclei with increasing undercooling. This is because diffusion processes in the melt and in the nucleus are necessary to form a nucleus or to allow it to grow, so that the atoms can attach to each other. With increasing undercooling, however, the diffusion processes due to the “sluggish” particles decrease. This applies to diffusion in the melt, diffusion across the phase boundary and diffusion within the nucleus. There are then no longer enough particles which could come together to form a nucleus and make it grow. As a result, fewer nuclei will form from a critical undercooling.
The diffusion-related agglomeration of the particles per time \(\dot N_d\) can be described by an Arrhenius ansatz that predicts an exponential dependence on temperature:
\begin{align}
\label{diffusion}
& \dot N_d \sim \text{exp}{\left(-\frac{Q_d}{k_B \cdot T}\right)} \\[5px]
\end{align}
\(Q_d\) denotes the temperature-independent activation energy for diffusion and \(k_B\) the Boltzmann constant.
At the same time, it must be considered that the particles must also reach the critical radius. Analogous to the equation (\ref{diffusion}), the number of nuclei formed per time \( \dot N_c\), which exceed the critical radius, can be determined:
\begin{align}
\label{keimzahl}
&\dot N_c \sim \text{exp}{\left(-\frac{\Delta G_c(\Delta T)}{k_B \cdot T}\right)} \\[5px]
\end{align}
\(\Delta G_c(\Delta T)\) denotes the temperature-dependent activation energy for nucleation.
The rate of nucleation \(\dot N_{n}\) ultimately depends on both influences, so that the total dependency is given by multiplying both equations:
\begin{align}
\label{keimbildungsrate}
&\boxed{\dot N_{n} \sim \text{exp}{\left(-\frac{Q_d}{k_B \cdot T}\right)} \cdot \text{exp}{\left(-\frac{\Delta G_c(\Delta T)}{k_B \cdot T}\right)}} \\[5px]
\end{align}
Note that the energy barrier for nucleation depends on undercooling. The figure below schematically shows the influence of undercooling on the nucleation rate according to the equation (\ref{keimbildungsrate}).
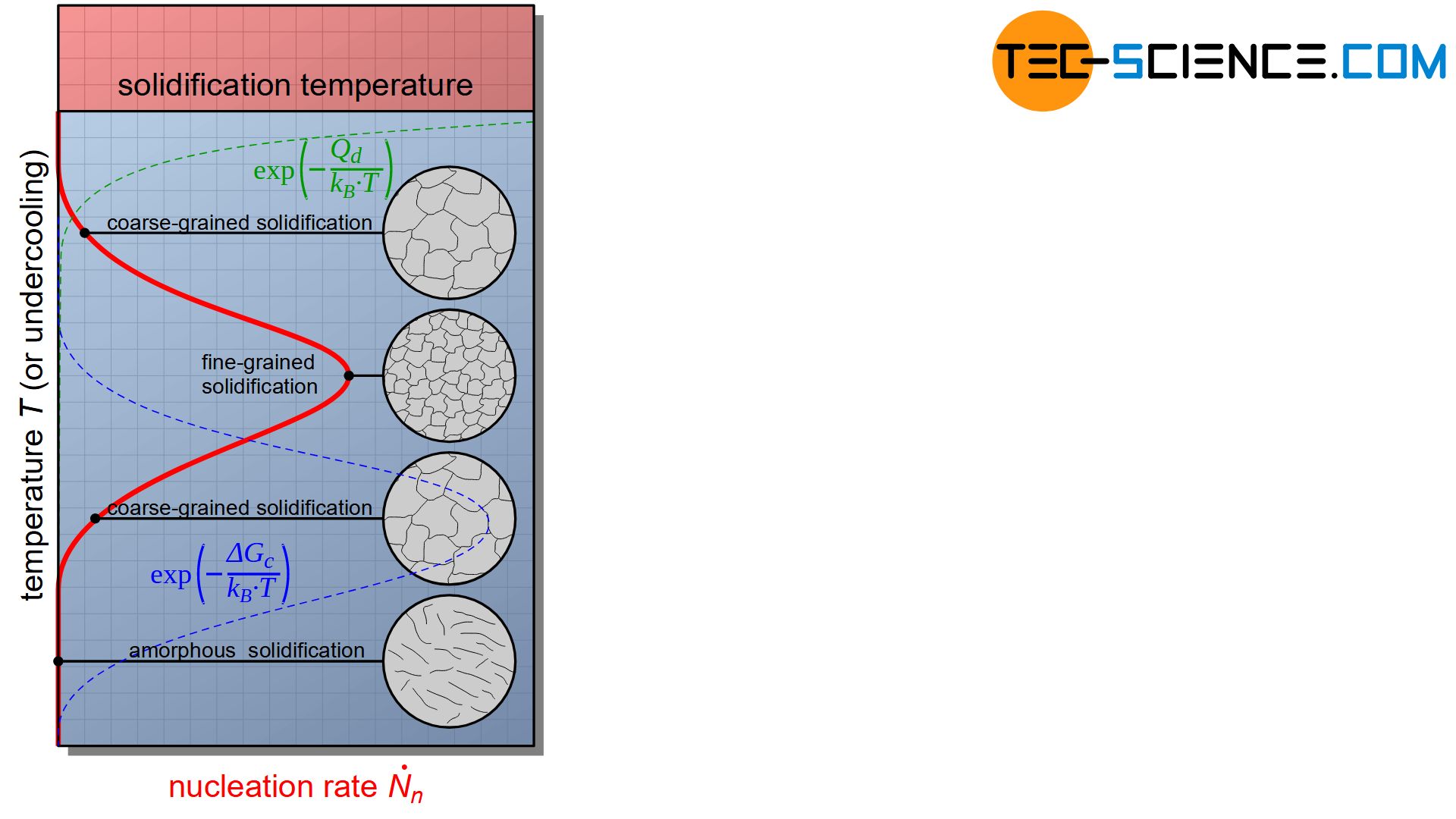
With low supercooling, the activation energy for nucleation \(\Delta G_c\) is considerably greater than the energy activation for diffusion \(Q_d\). The formation of nuclei is therefore inhibited by the great energy needed for nucleation.
If the undercooling is too high, the whole thing turns into the opposite. Due to the low temperature, the activation energy for diffusion \(Q_d\) is considerably greater and now inhibits the formation of a nucleus, although the energy barrier for nucleation \(\Delta G_c\) would be very low for this.
Consequently, there is a maximum of nucleation rate with a certain undercooling. By this optimal undercooling most nuclei can obviously form, which leads to an extremely fine-grained structure.
However, the diagram of the nucleation rate also shows that excessive undercooling can even completely suppress nucleation. Such a strong supercooled melt then solidifies without crystallization. The particles are “frozen” so to speak before they could have attached themselves to a crystal structure. Such metals are then also called amorphous metals (metallic glasses).