Vollkommene Löslichkeit der Komponenten im festen Zustand (Mischkristall-Legierung)

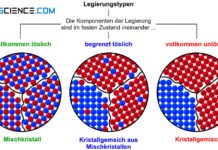
Sind die Komponenten einer Legierung im festen Zustand völlig löslich ineinander, dann bilden sich Mischkristalle.

Einleitung

Sind die beiden Komponenten eines Zweistofflegierungssystems (binäres System) im festen Zustand vollkommen ineinander löslich, so spricht man von einer Mischkristalllegierung. Für diesen Fall bilden die beiden Komponenten ein gemeinsames Kristallgitter, das sich sowohl aus den Atomen des Basisstoffes als auch aus den Legierungselementatomen aufbaut (nähere Informationen siehe Abschnitt Legierungstypen).

Das Legierungssystem Kupfer/Nickel weist eine solche vollkommene Mischbarkeit über den gesamten Konzentrationsbereich auf (lückenlose Mischkristallreihe). Im Folgenden soll deshalb das Legierungssystem Kupfer/Nickel exemplarisch als Beispiel einer Legierung mit vollkommener Löslichkeit der Komponenten im festen Zustand näher erläutert werden.

Eine vollkommene Löslichkeit der Komponenten im festen Zustand wird auch als Mischkristall (feste Lösung) bezeichnet!

Abkühlkurven

Wie bereits im Kapitel Kristallisationswärme erläutert, erstarrt ein Reinstoff in einem sogenannten Haltepunkt, d.h. die Temperatur bleibt während der Kristallisation konstant. Im Gegensatz hierzu weisen allerdings Stoffgemische im Allgemeinen keinen Haltepunkt während der Erstarrung mehr auf sondern einen sogenannten Knickpunkt.

Die Temperaturabnahme wird während der Kristallisation also nicht mehr gänzlich gestoppt sondern lediglich verlangsamt. Dies zeigt sich in den abgeknickten Temperaturverläufen bei den entsprechenden Abkühlkurven der unten abgebildeten Kupfer-Nickel-Legierungen.

Legierungen besitzen keinen Erstarrungspunkt sondern einen Erstarrungsbereich!

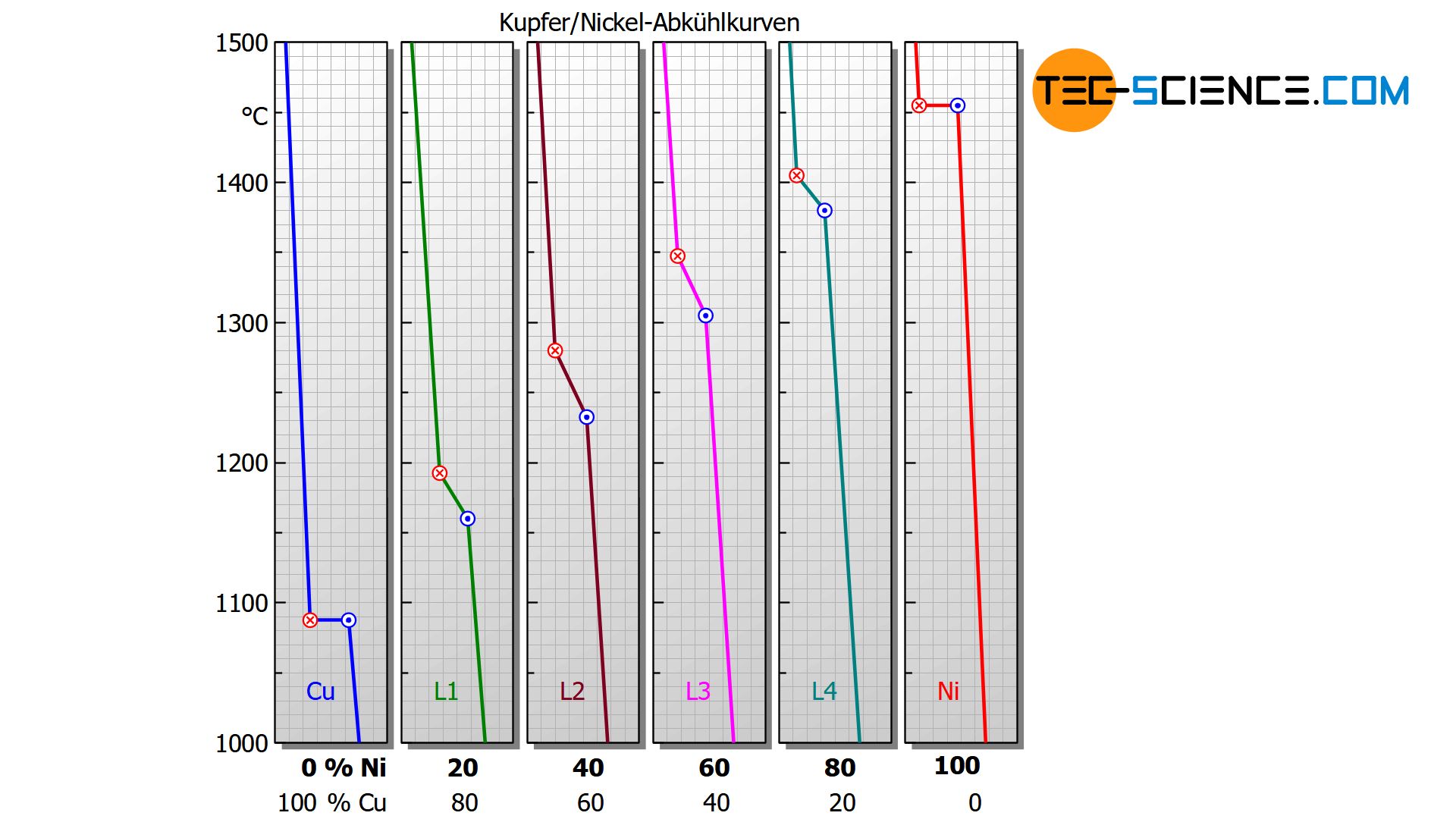
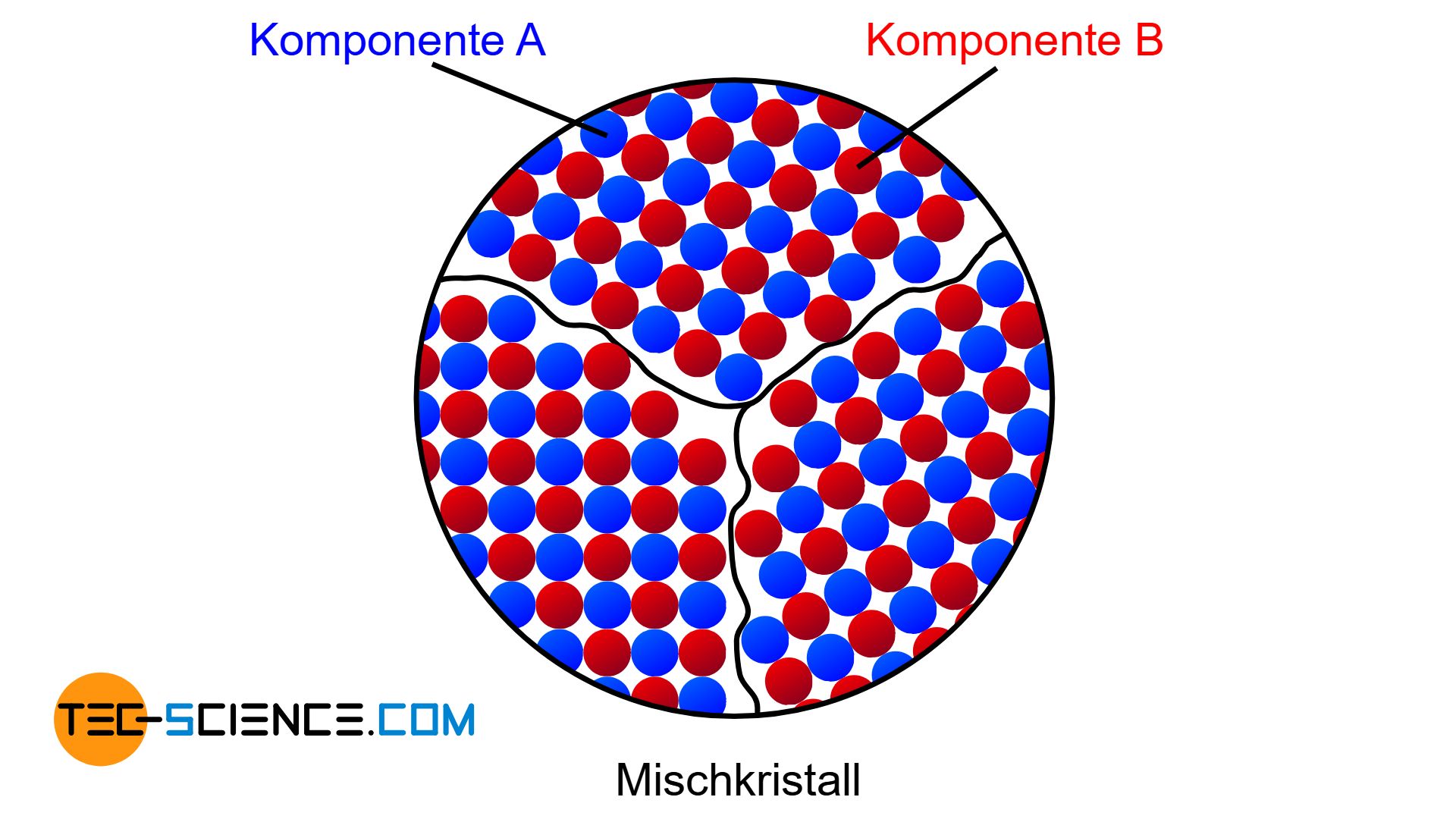
Darüber hinaus wird bei Betrachtung der Abkühlkurven ersichtlich, dass sich je nach Nickelgehalt der Erstarrungsprozess über unterschiedliche Temperaturbereiche erstreckt. Ausgehend des relativ niedrigen Schmelzpunktes des Kupfers (1085 °C) verschiebt sich der Erstarrungsbereich mit zunehmendem Nickelgehalt hin zu höheren Werten und gipfelt schließlich im Erstarrungspunkt des reinen Nickels (1455 °C).

Für einen Nickelgehalt von bspw. 20 % erstarrt die Legierung im Temperaturbereich zwischen ca. 1190 °C und 1160 °C, während bei einer Nickelkonzentration von 40 % die Erstarrung bereits bei rund 1280 °C einsetzt und schon bei ungefähr 1230 °C beendet ist.

Grund für die unterschiedlichen Erstarrungsbereiche ist, dass sich mit der Anwesenheit der Legierungselementatome auch die chemischen Eigenschaften – wie eben die Erstarrungstemperatur – ändern.

Legierungen können prinzipiell in unzählig vielen Konzentrationsvarianten hergestellt werden, je nachdem wie viel von der Legierungskomponente zum entsprechenden Basisstoff hinzu legiert wird. Dementsprechend ergibt sich auch eine unzählig große Variation an unterschiedlichen Erstarrungsbereichen. Um die Erstarrungbereiche über ein gesamtes Legierungssystem (d.h. für alle erdenklichen Legierungskonzentrationen) hinweg übersichtlich darzustellen, bedingt man sich sogenannter Phasendiagramme. Auf deren Erstellung soll im Folgenden näher eingegangen werden.

Phasendiagramm

Erstellen des Phasendiagramms

Um den Erstarrungsbereich von Legierungen in Abhängigkeit der Legierungskonzentration übersichtlich darzustellen, wählt man eine Diagrammform bei der auf der horizontalen Achse der Legierungsgehalt in Massenprozent (hier: Nickelgehalt) und auf der vertikalen Achse die Temperatur aufgetragen wird. Anschließend wird für ausgewählte Abkühlkurven der jeweilige Erstarrungsbeginn und das Erstarrungsende in das Diagramm eingetragen. Auf diese Weise erhält man zwei charakteristische Linienzüge, die den Erstarrungsbeginn (Liquiduslinie) und das Erstarrungsende (Soliduslinie) des gesamten Legierungssystems kennzeichnen.

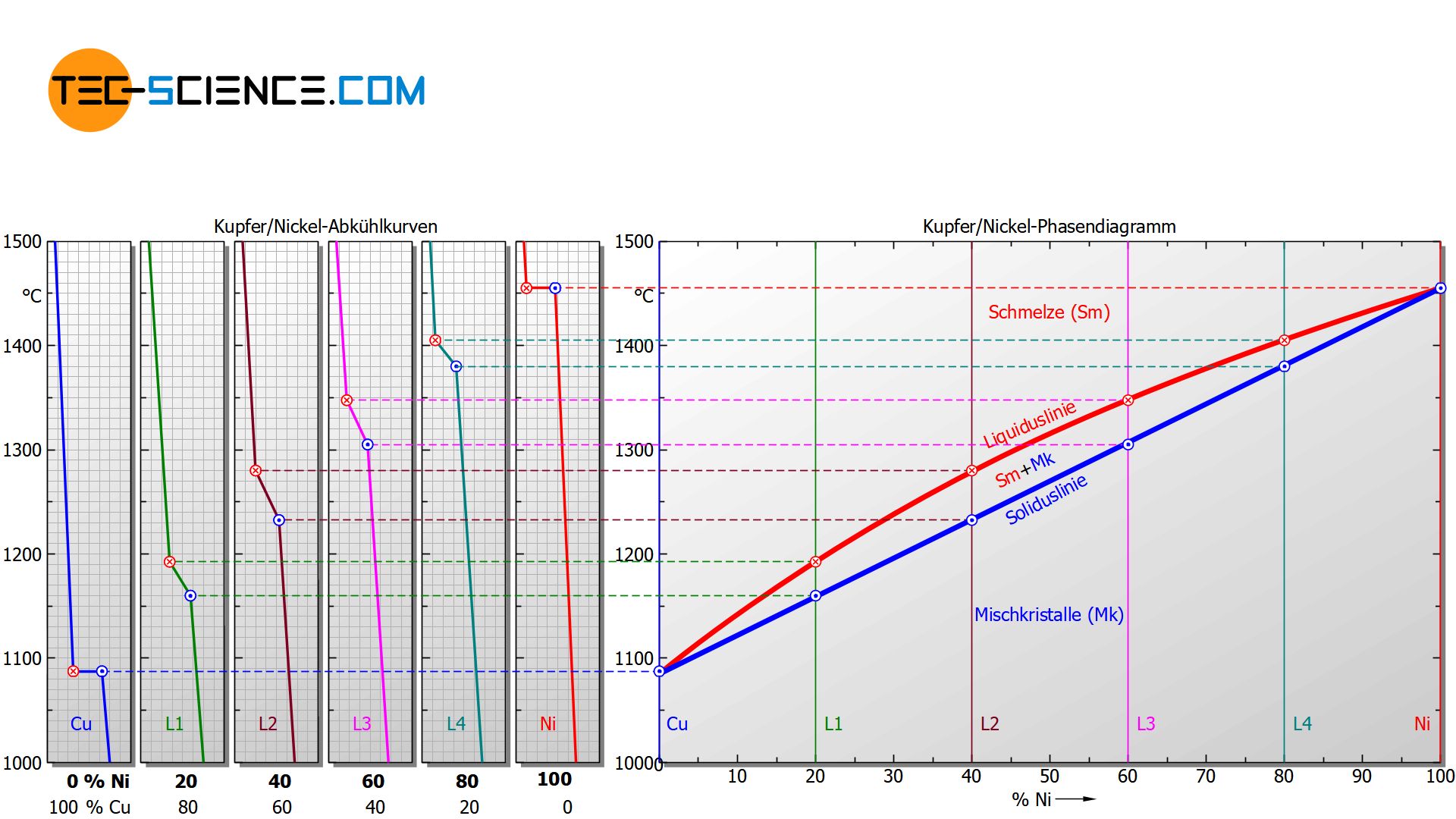
Oberhalb der Liquiduslinie ist die Legierung vollständig flüssig (Schmelze), während unterhalb der Soliduslinie das Gefüge vollständig erstarrt ist (Mischkristall)!

Beachte, dass der Grenzfall eines Nickelgehaltes von 0% letztlich dem Erstarrungspunkt des reinen Kupfers entspricht und ein Nickelgehalt von 100% dem des reinen Nickels. Da für diese Reinstoffe die Erstarrung bei konstanter Temperatur erfolgt, fallen dort Liquiduslinie und Soliduslinie zusammen.

Da in dieser Diagrammform die thermodynamischen Zustände einer Legierung deutlich werden, bezeichnet man ein solches Konzentrations-Temperatur-Diagramm auch als Zustandsdiagramm. Darüber hinaus werden die unterschiedlichen Zustände auch als Phasen bezeichnet und das Zustandsdiagramm deshalb auch oft Phasendiagramm genannt.

Als Phase bezeichnet man einen Zustand eines Stoffes, der sich durch eine einheitliche chemische und physikalische Struktur auszeichnet!

Beachte, dass diese Definition nicht nur die unterschiedlichen Aggregatzustände eines Stoffes einschließt, sondern eben auch deren atomare Struktur. So besteht Diamant und Graphit zwar jeweils aus Kohlenstoffatomen und beide liegen im selben festen Aggregatzustand vor, aber die chemische Struktur ist für Diamant und Graphit jeweils eine andere (Diamant: Diamantgitter, Graphit: hexagonales Gitter). In diesem Sinne stellen Diamant und Graphit also ebenfalls unterschiedliche Phasen dar.

Beachte, dass im Bereich zwischen der Liquiduslinie und der Soliduslinie zwei Phasen nebeneinander existieren – die flüssige Phase (Schmelze) und die bereits erstarrte Phase (Mischkristalle). Man bezeichnet diesen Zwischenbereich deshalb auch als Zweiphasengebiet.

Der Bereich zwischen Liquiduslinie und Soliduslinie wird auch als Zweiphasenbereich bezeichnet!

Lesen des Phasendiagramms

Am Beispiel einer Kupfer-Nickel-Legierung, bestehend aus 55% Nickel (CuNi55-Legierung), soll im Folgenden exemplarisch auf das Lesen und Interpretieren des Phasendiagrammes bei verschiedenen Temperaturen näher eingegangen werden.

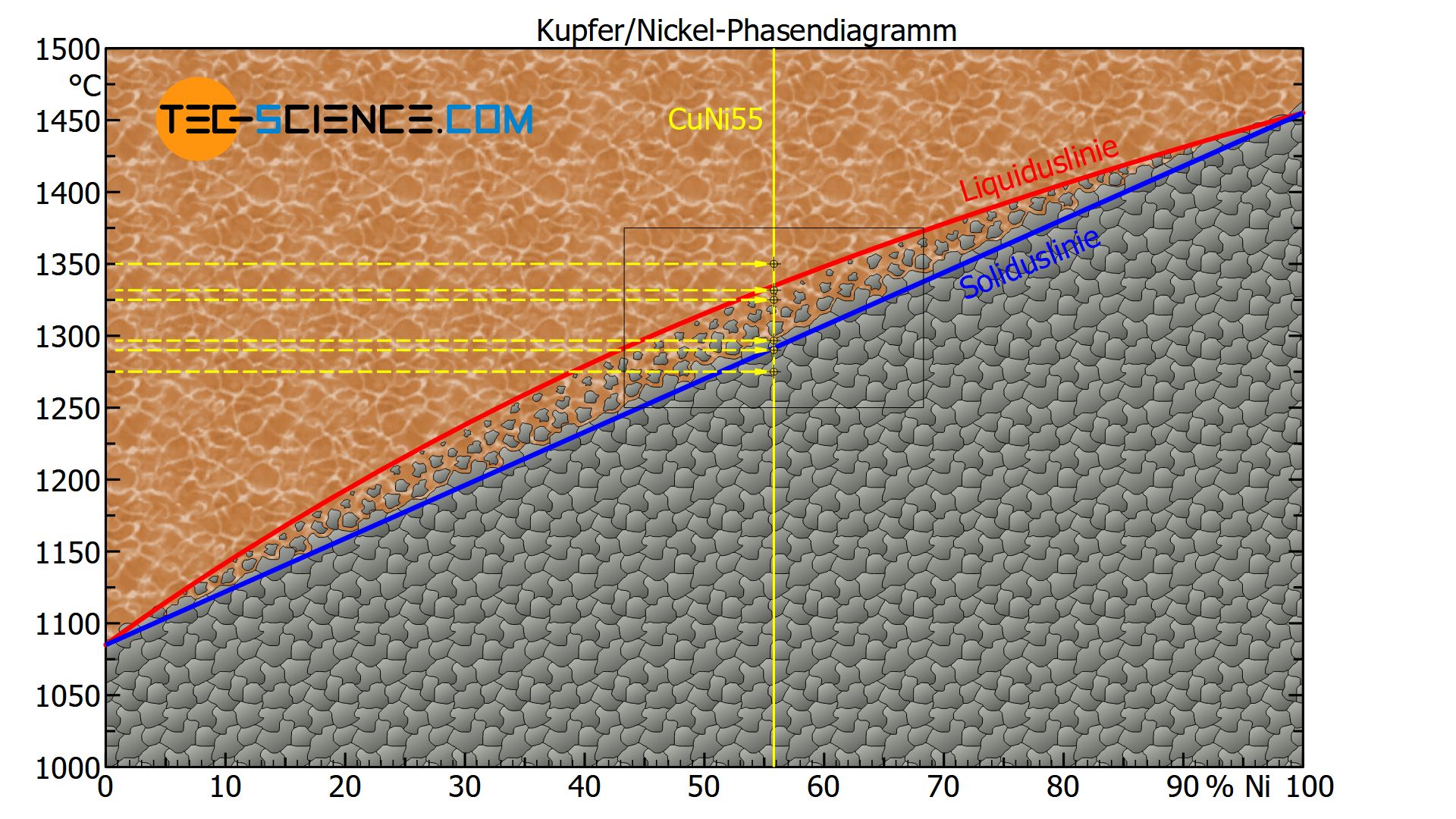
Aufgrund einer besseren Orientierung wird die Legierung zunächst als Zustandslinie in das Phasendiagramm eingetragen (gelbe Volllinie). Um nun für verschiedene Temperaturen die entsprechenden Zustände der Legierung zu lokalisieren dient eine horizontale Linie bei der jeweiligen Temperatur (gelbe Strichlinie). Der Schnittpunkt beider Linien gibt schließlich den Zustandspunkt wieder, d.h. der Zustand wie die Legierung bei dieser Temperatur vorzufinden ist.

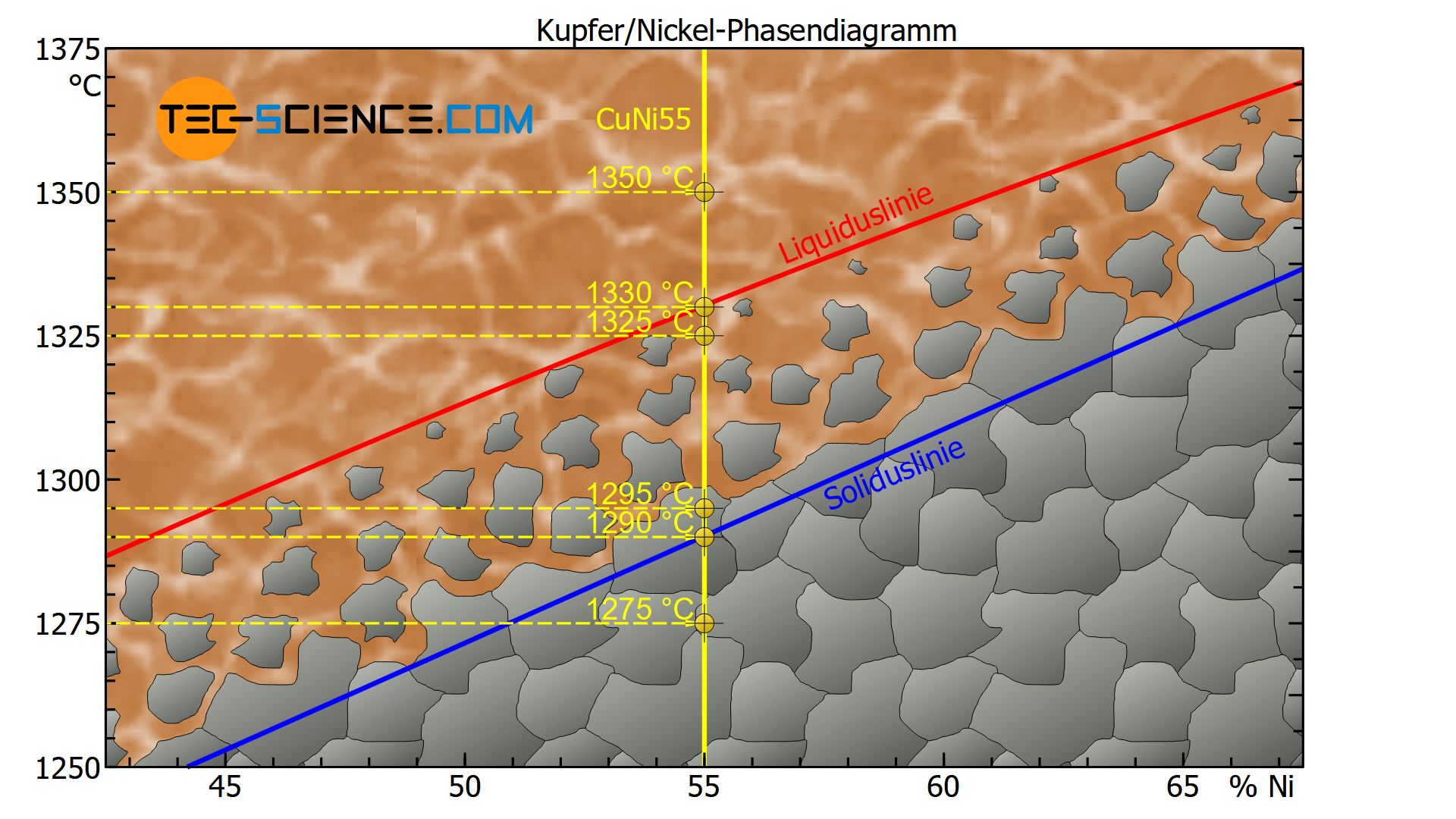
Bei einer Temperatur von bspw. 1350 °C befindet sich der Zustandspunkt der CuNi55-Legierung oberhalb der Liquiduslinie. Die Legierung liegt somit vollständig im flüssigen Zustand vor.

Bei einer Temperatur von rund 1330 °C befindet sich der Zustandspunkt auf der Liquiduslinie. Der Kristallisationsprozess setzt ausgehend an vorhandenen Keime ein und das Gefüge beginnt sich zu bilden (Erstarrungsbeginn).

Bei einer Temperatur von 1325 °C liegt der Zustandspunkt knapp unterhalb der Liquiduslinie im Zweiphasengebiet. Der Erstarrungsprozess hat also gerade erst begonnen und es haben sich einige wenige Kristalle gebildet, der Großteil ist allerdings noch flüssig.

Bei einer Temperatur von 1295 °C liegt der Zustandspunkt knapp oberhalb der Soliduslinie im Zweiphasengebiet. Der Kristallisationsprozess ist folglich fast abgeschlossen, sodass die Kristallite auf Kosten der Schmelze gewachsen sind, d.h. das Gefüge ist fast vollständig erstarrt.

Bei der angegebenen 55%-igen Kupfer-Nickel-Legierung liegt der Zustandspunkt bei einer Temperatur von rund 1290 °C direkt auf der Soliduslinie und das Gefüge ist somit vollständig erstarrt und liegt als Mischkristallgefüge vor.

Bei weiterer Abkühlung auf bspw. 1275 °C liegt der Zustandspunkt unterhalb der Soliduslinie. Das Gefüge ändert sich dabei nicht mehr weiter. Im Schliffbild sind die typischen Körner mit ihren Korngrenzen zu erkennen.

Gültigkeitsbereich

Beachte, dass die beiden Phasen im Zweiphasengebiet – Schmelze und Mischkristalle – stabil nebeneinander existieren, d.h. es handelt sich um einen thermodynamisch stabilen Zustand. Zwar kann es sein, dass bereits erstarrte Bereiche sich teilweise wieder verflüssigen, aber dabei kristallisieren gleichzeitig im selben Maße flüssige Bereiche wieder zu festen Gefügebestandteilen („breiiger Zustand“). Es handelt sich also um ein thermodynamisches Gleichgewicht, bei dem zwar auf mikroskopischer Ebene Umkristallisationsvorgänge stattfinden, im makroskopischen Maßstab sich allerdings nichts ändert.

Da das Einstellen eines Gleichgewichtszustandes Zeit benötigt (aufgrund von Diffusionsprozessen), müssen die Abkühlkurven für das Aufstellen eines Phasendiagramms im Prinzip bei (unendlich) langsamer Abkühlung aufgenommen werden. Nur dann ist stets gewährleistet, dass sich das System immer im thermodynamischen Gleichgewicht mit der Umgebung befindet. Bei zu schneller Abkühlung hingegen kann sich der Gleichgewichtszustand nicht einstellen und die Erstarrungstemperaturen bzw. -bereiche (d.h. Liquidus- und Soliduslinie) verschieben sich! Phasendiagramme gelten also strenggenommen immer nur für (unendlich) langsame Abkühlprozesse. Insofern gibt das Zustandsdiagramm lediglich Zustände im thermodynamischen Gleichgewicht wieder.

Bestimmung der Phasenzusammensetzung

Während der Erstarrung einer Legierung, ändert sich sowohl die chemische Zusammensetzung der Schmelze als auch die der Mischkristalle ständig. Die chemische Zusammensetzung dieser einzelnen Phasen wird auch Phasenzusammensetzung genannt.

Als Phasenzusammensetzung bezeichnet man die chemische Zusammensetzung der einzelnen Phasen (Schmelze und Mischkristalle)!

Man kann sich hierzu vorstellen als würde man die noch flüssige Schmelze von den bereits erstarrten Mischkristallen „absieben“ und anschließend in getrennten Behältnissen auf deren chemische Zusammensetzung untersuchen.

Am Beispiel der bereits im Abschnitt zuvor betrachteten CuNi55-Legierung soll die Bestimmung der Phasenzusammensetzung anhand des Zustandsdiagrammes erläutert werden.

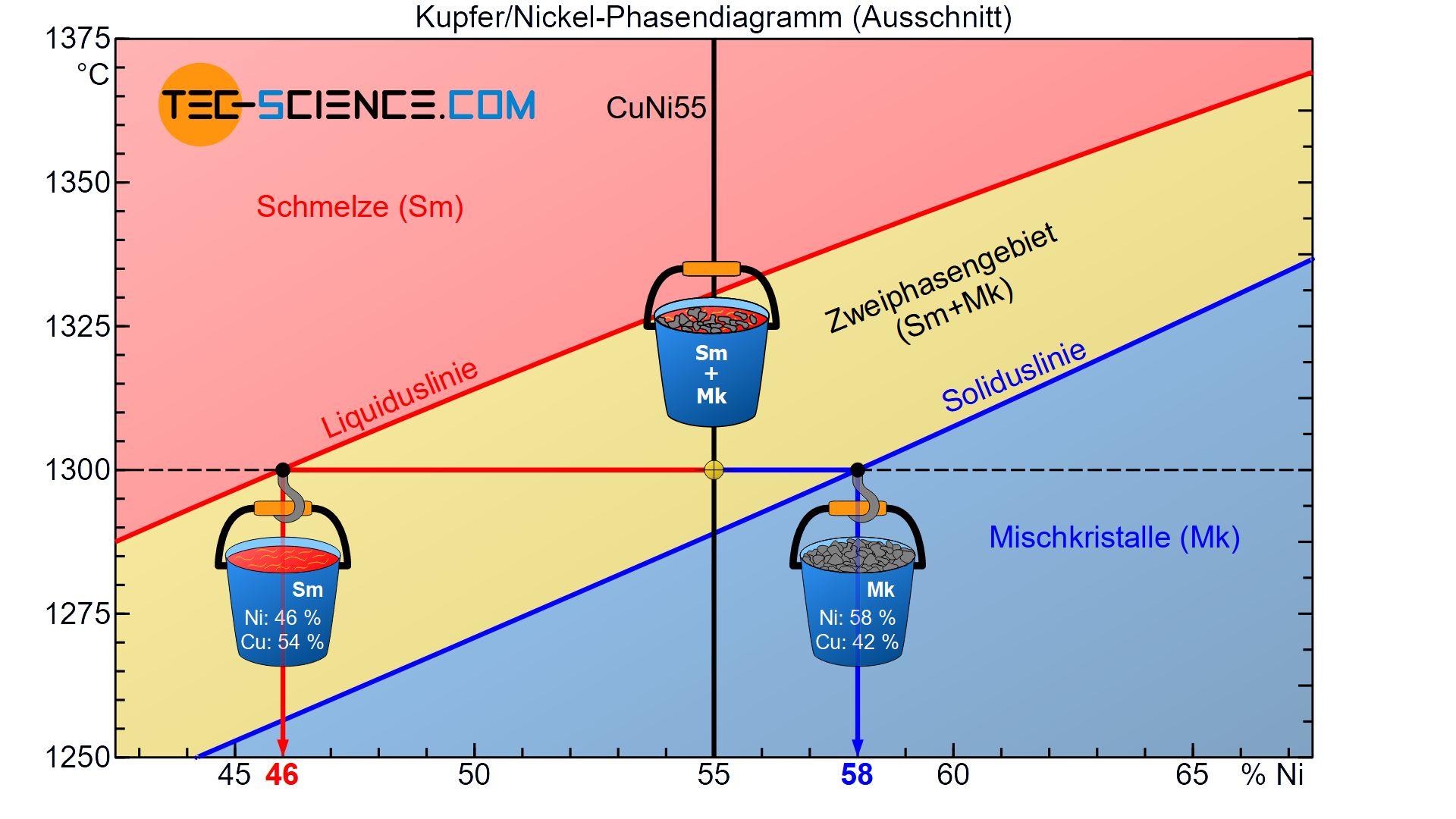
Hierzu wird der Zustand der Legierung bei einer Temperatur von 1300 °C betrachtet. Dieser Zustandspunkt liegt im Zweiphasengebiet, sodass Teile der Legierung als Schmelze und als Mischkristall vorliegen. Sowohl die Schmelze als auch die bereits gebildeten Mischkristall weisen dabei unterschiedliche chemische Zusammensetzungen auf. Diese können wie folgt ermittelt werden.

Ausgehend des Zustandspunktes wird auf der horizontalen Temperaturlinie (schwarze Strichlinie) zunächst jeweils soweit verfahren, bis die jeweilige Phasengrenze erreicht wird (Liquiduslinie bzw. Soliduslinie).

Durch Fällen des Lotes auf die Konzentrationsachse kann nun die entsprechende chemische Zusammensetzung der Restschmelze und der Mischkristalle direkt abgelesen werden. In diesem Fall bestehen die bereits erstarrten Mischkristalle im Mittel aus 58 % Ni (bzw. 42 % Cu) und die noch flüssige Restschmelze im Mittel aus 46 % Ni (bzw. 54 % Cu).

Beachte, dass die erhaltenen chemischen Konzentrationen keinen Widerspruch zur gesamten Legierungskonzentration mit 55 % Nickel darstellen. Zwar haben die Mischkristalle einen höheren Nickelgehalt (58 %) als die eigentliche Legierung, dafür besitzt die Schmelze allerdings eine geringere Nickelkonzentration (46 %).

Für die Bestimmung des gesamten Nickelgehalts darf an dieser Stelle nicht einfach der Mittelwert aus beiden Konzentrationen gebildet werden. Diese Überlegung wäre nur dann gerechtfertigt, wenn Schmelze und Mischkristalle zu gleichen Teilen vorliegen würden.

In dem betrachteten Zustandspunkt liegen allerdings mehr Mischkristalle als Schmelze vor. Folglich fällt die höhere Nickelkonzentration der Mischkristalle mit 58 % Nickel stärker ins Gewicht als der Nickelgehalt der Schmelze. Anteilsmäßig gewichtet, ergäbe die Nickelkonzentration über die gesamte Legierung hinweg schließlich wieder die geforderten 55 %!

Bestimmung der Phasenanteile (Konodenregel)

Im Abschnitt zuvor wurde die Bestimmung der chemischen Zusammensetzung von Schmelze und Mischkristallen anhand des Zustandsdiagramms erläutert. Unbeantwortet ist bisher noch die Frage wie viel Prozent der gesamten Legierung bei einer bestimmten Temperatur noch flüssig ist (d.h. als Schmelze vorliegt) und wie viel Prozent bereits erstarrt ist (d.h. als Mischkristalle vorliegen).

Man kann sich hierzu wieder anschaulich vorstellen, dass die teilweise bereits erstarrte Legierung in Gedanken von der Restschmelze abgesiebt wird. Nun werden die abgesiebten Mischkristalle und die flüssige Restschmelze getrennt gewogen und deren jeweiligen Massenanteile am Gesamten bestimmt.

Man redet in diesem Zusammenhang auch vom sogenannten Phasenanteil, d.h. der massenmäßige Anteil zwischen den Phasen Schmelze und Mischkristalle. Der Phasenanteil kann ebenfalls anhand des Zustandsdiagramms ermittelt werden, wie im Folgenden erläutert wird.

Als Phasenanteil bezeichnet man den prozentualen Anteil der jeweiligen Phasen an der gesamten Legierung!

Da die umgesetzten Wärmeenergien an die jeweiligen Massen der Phasen gekoppelt sind, lassen sich die Phasenanteile mithilfe des Hebelgesetzes bestimmen (auch Konodenregel genannt). Hierzu wird exemplarisch wieder die CuNi55-Legierung bei einer Temperatur von 1300 °C betrachtet.

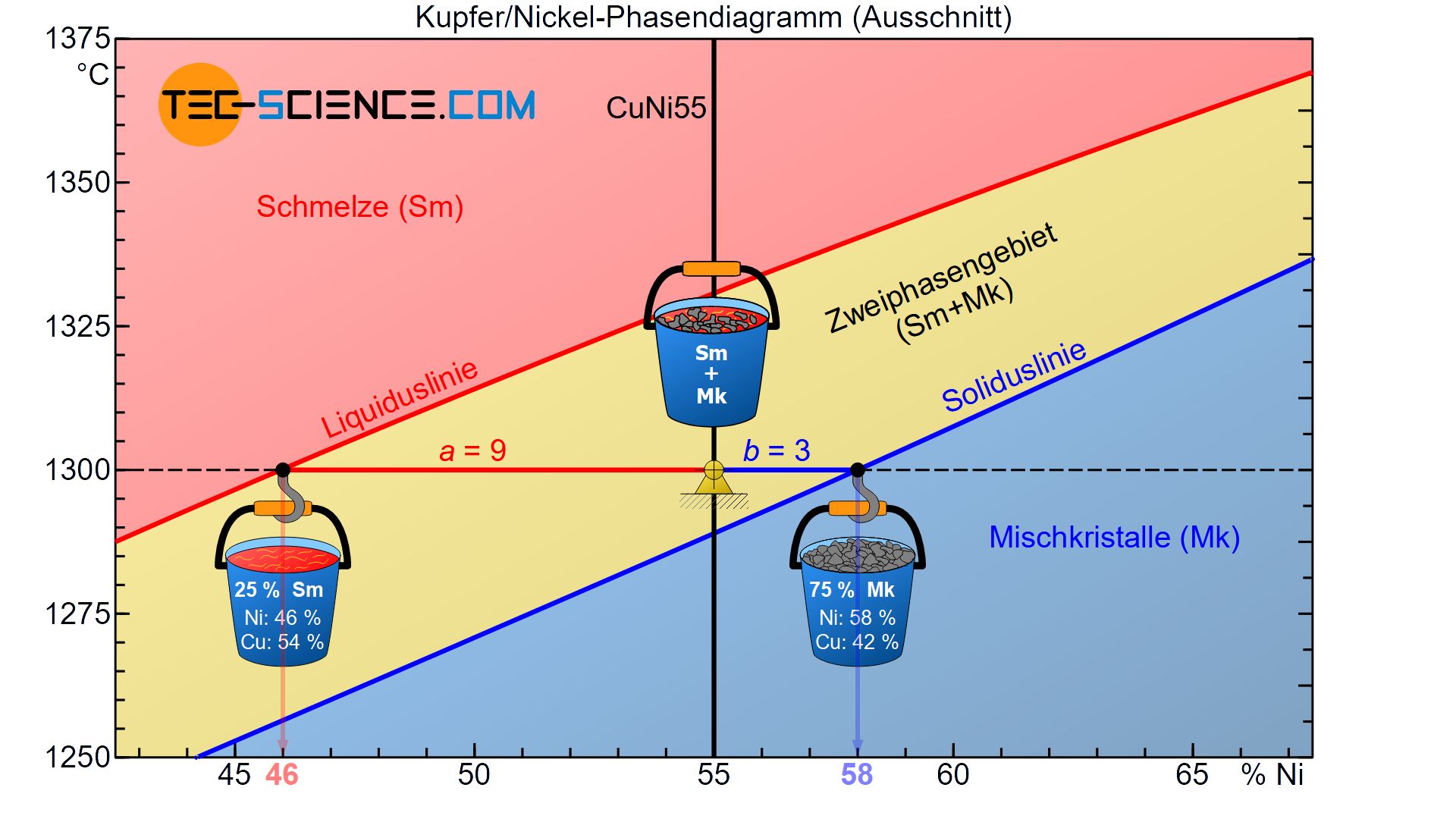
Ausgehend des betrachteten Zustandspunktes bilden die entsprechenden Abstände hin zur Liquidus- bzw. Soliduslinie die Hebelarme einer gedachten Balkenwaage. Der Drehpunkt dieser Balkenwaage befindet sich im Zustandspunkt.

In Gedanken werden nun an den Hebelenden die jeweiligen Behältnisse mit den abgesiebten Phasen angehängt. Dabei wird das Behältnis mit den bereits erstarrten Mischkristallen auch an die Phasengrenze hin zu den Mischkristallen gehängt (Soliduslinie). Der Schmelzebehälter wird entsprechend an die zum Schmelzbereich angrenzende Liquiduslinie angebracht.

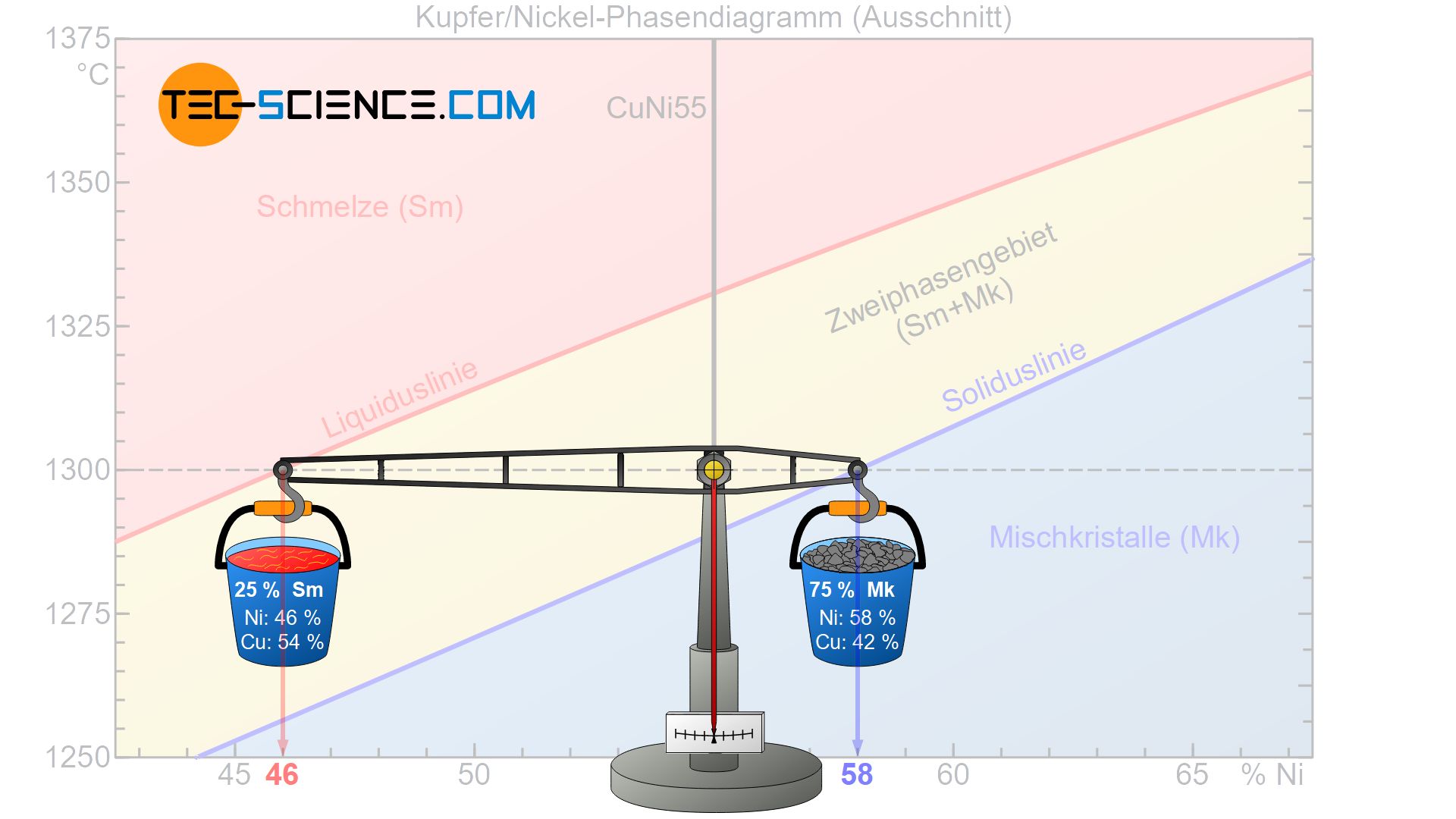
Nun kann das Gleichnis der Waage herangezogen werden, um die jeweiligen Phasenanteile zu bestimmen. In der anschaulichen Vorstellung ist es dabei vorteilhaft von einer Legierungsmasse von 100 kg auszugehen. Somit stellt sich in dem Zusammenhang die Frage wie viel von dieser Gesamtmasse auf die jeweiligen Hebelarme entfällt, um sich im Gleichgewicht zu befinden.

Wird die Schmelzmasse mit \(Sm\) bezeichnet und die Masse der Mischkristalle mit \(Mk\), so liefert das Hebelgesetz zunächst den folgenden Zusammenhang mit den entsprechenden Hebelarmen \(a\) und \(b\):

\begin{align}
\label{hebelgesetz}
& Sm \cdot a = Mk \cdot b  \\[5px]
\end{align}

Als weitere Bedingung kommt schließlich noch hinzu, dass der Massenanteil an Schmelze und Mischkristalle zusammen 100 % ergeben muss (in der anschaulichen Vorstellung entspricht dies dem Einsatz von 100 kg Legierungsmasse):

\begin{align}
\label{massengesetz}
& Sm + Mk = 100 \text{ %}  \\[5px]
\end{align}

Die beiden Bedingungen können nun ineinander eingesetzt und jeweils nach den gesuchten Größen \(Sm\) bzw. \(Mk\) aufgelöst werden:

\begin{align}
\underline{Sm \cdot a  = Mk \cdot b} ~~~\text{mit}~~~\underline{Mk = 100 \text{ %} -Sm} ~~~\text{folgt:} \\[5px]
\end{align}

\begin{align}
Sm \cdot a &= (100 \text{ %} – Sm) \cdot b  \\[5px]
Sm \cdot a &= 100 \text{ %} \cdot b – Sm \cdot b  \\[5px]
Sm \cdot a + Sm \cdot b &= 100 \text{ %} \cdot b   \\[5px]
Sm \cdot (a+b) &= 100 \text{ %} \cdot b   \\[5px]
\end{align}

\begin{align}
\label{Sm}
\boxed{Sm = \frac{b}{a+b} \cdot 100 \text{ %}}   \\[5px]
\end{align}

Auf die analoge Weise erhält man den Phasenanteil der Mischkristalle:

\begin{align}
\underline{Sm \cdot a  = Mk \cdot b} ~~~\text{mit}~~~\underline{Sm = 100 \text{ %} -Mk} ~~~\text{folgt:} \\[5px]
\end{align}

\begin{align}
(100 \text{ %} – Mk) \cdot a &= Mk \cdot b  \\[5px]
100 \text{ %} \cdot a – Mk \cdot a &= Mk \cdot b  \\[5px]
100 \text{ %} \cdot a  &= Mk \cdot b + Mk \cdot a  \\[5px]
100 \text{ %} \cdot a  &= Mk \cdot (a+b) \\[5px]
\end{align}

\begin{align}
\label{Mk}
\boxed{Mk = \frac{a}{a+b} \cdot 100 \text{ %}}   \\[5px]
\end{align}

Die Ergebnisse können schließlich wie folgt interpretiert werden. Der Anteil einer Phase bestimmt sich immer über die Länge des gegenüberliegenden Hebelarms geteilt durch die Gesamtlänge des Hebels (auch als Konode bezeichnet)!

Der Phasenanteil ergibt sich über die Formel „gegenüberliegender Hebelarm geteilt durch die Konodenlänge“ (Konodenregel)!

Dieser Merksatz ist wesentlich einprägsamer als die entsprechenden Formeln, zumal die Bezeichnung der Hebellängen \(a\) und \(b\) willkürlich gewählt wurde und sich bei Vertauschen auch die jeweiligen Formeln ändern würden.

In dem vorliegenden Fall besitzt der gegenüberliegende Hebelarm des Mischkristallbehältnisses \(a=9\) und die gegenüberliegende Hebellänge des Schmelzbehälters \(b=3\) (dabei beziehen sich die Hebellängen auf den Abstand der jeweiligen Konzentrationswerte). Somit ergibt sich eine Konodenlänge von \(a+b=12\). Mit diesen Werten kann nun der Phasenanteil der Schmelze bzw. der Mischkristalle ermittelt werden:

\begin{align}
\underline{Sm} = \frac{b}{a+b} \cdot 100 \text{ %} = \frac{3}{12} \cdot 100 \text{ %} = \underline{25 \text{ %}}   \\[5px]
\underline{Mk} = \frac{a}{a+b} \cdot 100 \text{ %} = \frac{9}{12} \cdot 100 \text{ %} = \underline{75 \text{ %}}   \\[5px]
\end{align}

Demzufolge liegt in dem betrachteten Zustandspunkt 25 % der Legierungsmasse als Schmelze vor, während die restlichen 75 % der Legierung bereits erstarrt sind und somit als Mischkristalle vorliegen. Die Phasenanteile addiert müssen in Summe natürlich wieder 100 % ergeben. Beachte, dass sich mit sinkender Temperatur das Gleichgewicht kontinuierlich hin zu einem größeren Mischkristallanteil verschiebt und somit auch hieraus ersichtlich wird, dass das Gefüge mehr und mehr erstarrt.

Um die bisher ermittelten Zahlen etwas anschaulicher zu gestalten, wird nun von einer Legierungsmasse von insgesamt 100 kg ausgegangen. Übertragen auf den vorliegenden Zustand, sind somit 75 kg der Legierung bereits erstarrt, während 25 kg noch in flüssiger Form vorliegen. Wie im Abschnitt Phasenzusammensetzung bereits ermittelt, bestehen die vorliegenden 75 kg Mischkristalle im Mittel aus 58 % Nickel, während die Schmelze einen Nickelgehalt von 45 % aufweist.

In den Mischkristallen befindet sich somit eine Nickelmasse von 43,5 kg (=75 kg x 0,58) und in der Schmelze eine Nickelmasse von 11,5 kg (=25 kg x 0,46). In Summe beinhaltet die Legierung somit insgesamt eine Nickelmasse von 55 kg (=43,5 kg + 11,5 kg). Dies entspricht schließlich genau der Masse an Nickel für eine CuNi55-Legierung, die wie gefordert bei einem Legierungseinsatz von 100 kg zu insgesamt 55 kg aus Nickel besteht.

Seigerungen

Wird eine flüssige Kupfer-Nickel-Legierung abgekühlt, so stellt man bei einer anschließenden Werkstoffuntersuchung oft fest, dass sich der Nickelgehalt innerhalb eines Korns je nach Ort teilweise stark von anderen Kornbereichen unterscheidet. Während sich die Kornmitte bspw. durch einen relativ hohen Nickelgehalt auszeichnet, sind die Randbereiche des Korn bspw. eher nickelarm. Solche Konzentrationsunterschiede innerhalb eines Korns nennt man Kristallseigerung oder Mikroseigerung oder kurz Seigerung.

Kristallseigerungen sind Unterschiede in der chemischen Zusammensetzung innerhalb eines Korns!

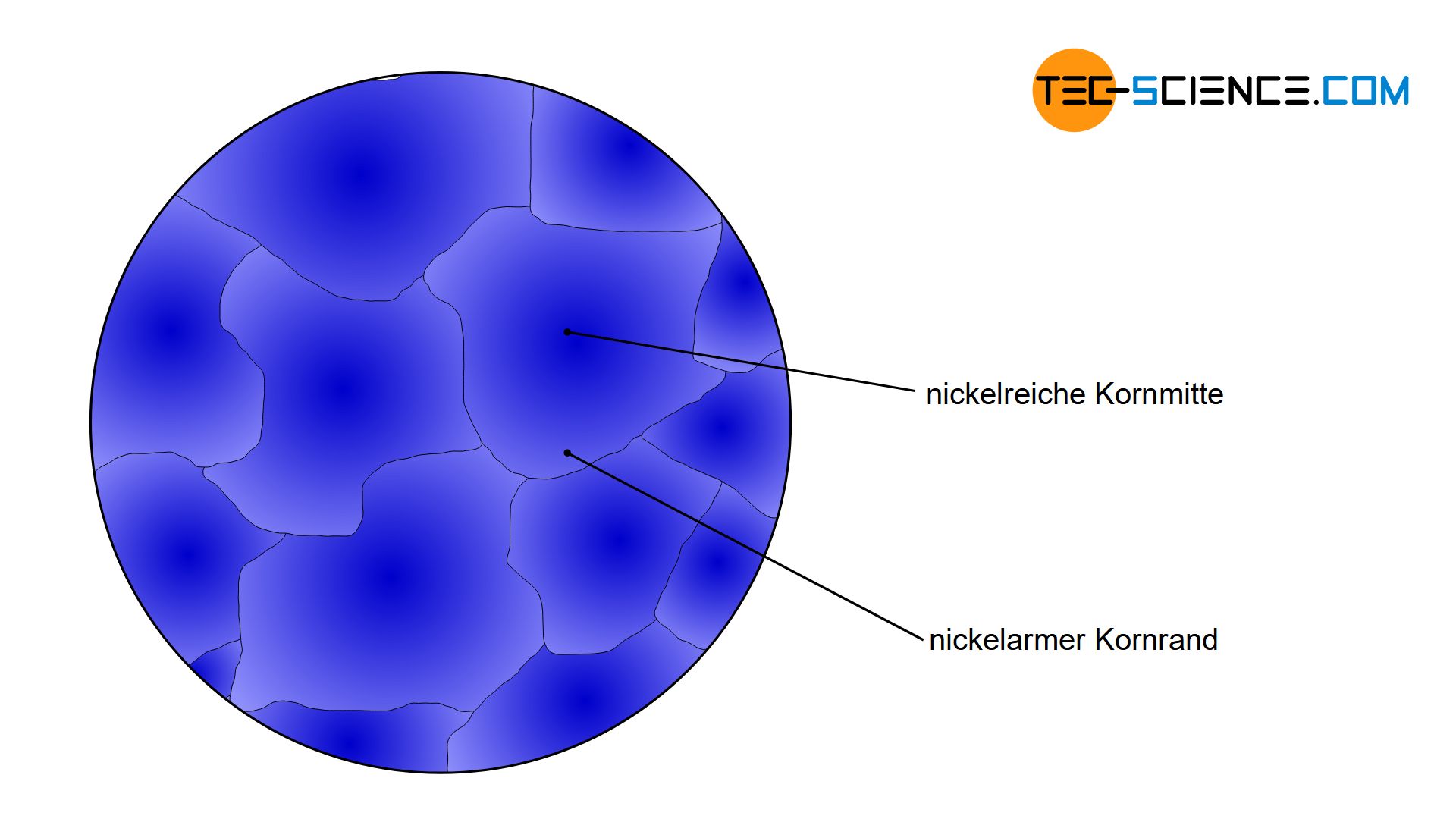
Da die Legierungskonzentration allerdings maßgeblich die Werkstoffeigenschaften bestimmt, zeigt die Kornmitte somit eine andere Eigenschaft (z.B. härter und fester) als der Randbereich (z.B. weicher und zäher). Solche unterschiedlichen Eigenschaften innerhalb eines Korns sind in der Regel nicht erwünscht, da dies zu unvorhersehbarem Materialversagen führen kann.

Die Bildung von Seigerungen kann mit Hilfe der im Abschnitt Phasenzusammensetzung erläuterten Gesetzmäßigkeiten relativ einfach nachvollzogen werden. Um die Entstehung von Seigerungen zu erläutern, wird an dieser Stelle wieder die CuNi55-Legierung mit 55 % Nickel betrachtet.

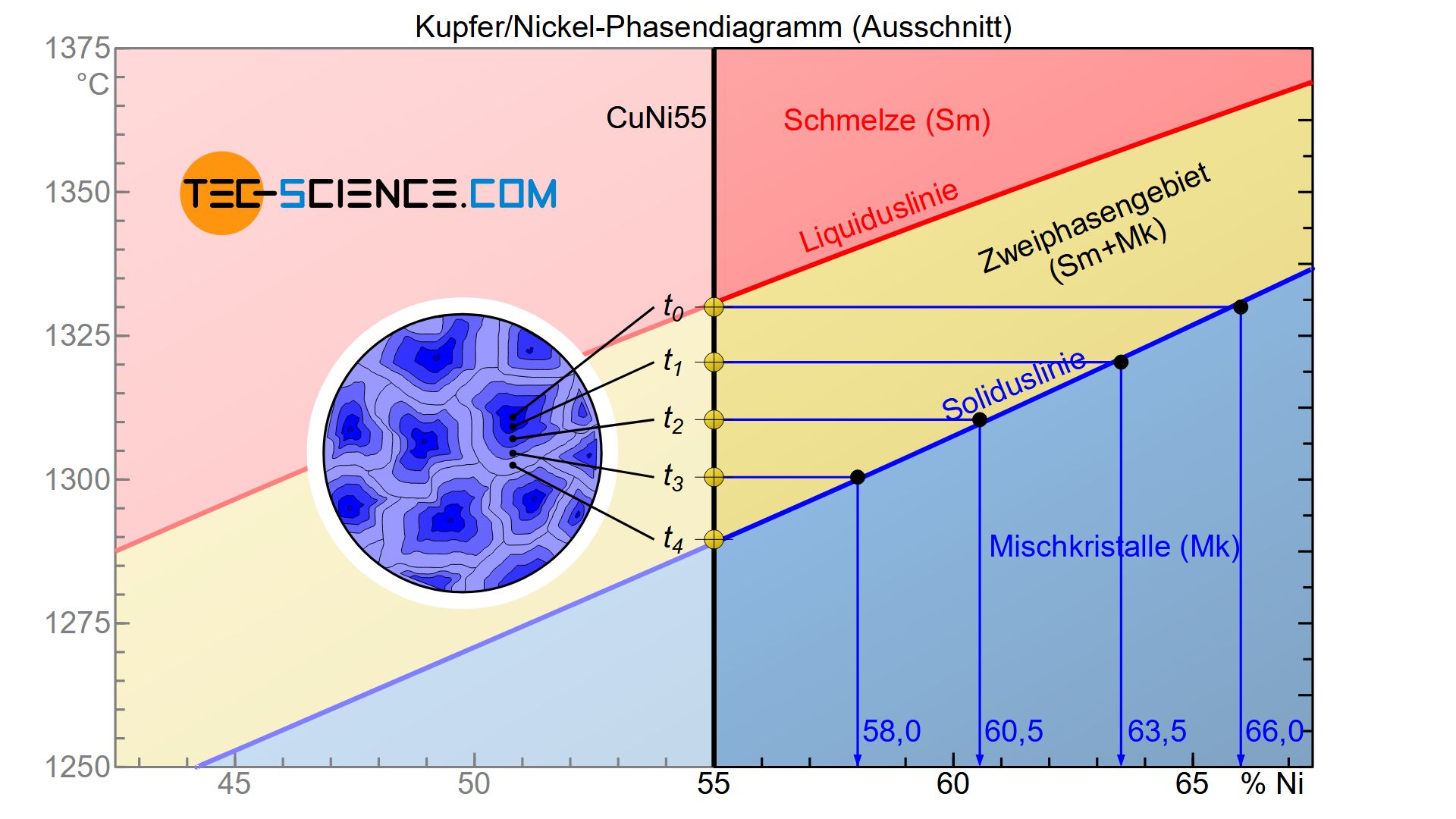
Aus dem Phasendiagramm wird ersichtlich, dass während der Erstarrung die Nickelkonzentration innerhalb der entstehenden Mischkristalle mit der Zeit abnimmt. So besitzen die ersten entstehenden Mischkristalle unmittelbar bei Einsetzen der Erstarrung zum Zeitpunkt \(t_0\) einen Nickelgehalt von rund 66 %.

Bei weiterer Abkühlung lagern sich um die bereits entstandenen Mischkristalle weitere Atome aus der Schmelze an. Zu einem späteren Zeitpunkt \(t_1\) hat sich schließlich eine neue Schicht angelagert, die gemäß dem Zustandsdiagramm zu einem mittleren Nickelgehalt im gesamten Korn von nur noch 63,5 % führt. Da es sich dabei um einen Durchschnittswert innerhalb des gesamten Mischkristalls handelt, muss die angelagerte Schicht offensichtlich einen geringeren Nickelgehalt als die zuvor erstarrte Schicht aufweisen. Nur so kann das Sinken des mittleren Nickelgehaltes erklärt werden.

Schließlich führt das Voranschreiten der Erstarrung zu einer weiteren Abnahme des mittleren Nickelgehaltes in den Mischkristallen (\(t_1\)→\(t_2\)→\(t_3\)). Ist der Erstarrungsprozess zum Zeitpunkt \(t_4\) abgeschlossen, so ist der Nickelgehalt schließlich auf 55 % gesunken und liegt nun vollständig im erstarrten Gefüge vor.

In der Realität lagern sich die Atomschichten natürlich nicht schrittweise sondern kontinuierlich um die bereits erstarrten Mischkristalle an. Folglich erhält man auch eine kontinuierliche Abnahme der Nickelkonzentration ausgehend der Kornmitte (Erstarrungsbeginn) bis hin in die entsprechenden Randbereiche (Erstarrungsende). Auf diese Weise lässt sich das Zustandekommen von Seigerungen erklären.

Beachte, dass Seigerungen kein reines Phänomen von Kupfer-Nickel-Legierungen sind, sondern ein prinzipielles Verhalten von Mischkristalllegierungen!

Seigerungen ließen sich grundsätzlich durch eine hinreichend langsame Abkühlung vermeiden, da sich hierdurch die entstehenden Konzentrationsunterschiede durch Diffusionsprozesse stets ausgleichen können. In der Realität können Abkühlprozesse allerdings nicht unendlich langsam erfolgen, sodass sich unweigerlich Konzentrationsunterschiede im Gefüge ergeben. In solchen Fällen können durch eine nachträgliche Wärmebehandlung bei hinreichend hohen Temperaturen (Diffusionsglühen genannt) die entstandenen Konzentrationsunterschiede teilweise wieder ausgeglichen werden.