Für Stähle können die Gefüge- und Phasenanteile im Eisen-Kohlenstoff-Diagramm mit Hilfe des Hebelgesetzes ermittelt werden.
Einleitung
Für viele Anwendungen ist es wichtig, genau zu wissen aus welchen Gefüge- bzw. Phasenanteilen sich ein Stahl bei einer bestimmten Kohlenstoffkonzentration zusammensetzt. Dies macht letztlich eine Berechnung notwendig. Um diese Durchführen zu können, muss allerdings das gesamte Eisen-Kohlenstoff-Diagramm betrachtet werden. Deshalb wird im Folgenden kurz auf das vollständige Phasendiagramm des metastabilen Systems eingegangen, bevor abschließend die Berechnung der Gefüge- bzw. Phasenanteile erläutert wird.
Bisher wurde das Eisen-Kohlenstoff-Diagramm nur bis zu einem Kohlenstoffgehalt von 2 % betrachtet (Stahlecke). Bei höheren Kohlenstoffkonzentrationen treten weitere Phasenumwandlungen auf, welche zu einem anderen Grundgefüge führen. Solche Eisenwerkstoffe werden dann nicht mehr als Stähle sondern als Gusseisen bezeichnet. Im entsprechenden Kapitel Gusseisen wird auf die Gefügeentstehung solcher Eisenwerkstoffe näher eingegangen.

Grundsätzlich endet das Eisen-Kohlenstoff-Diagramm des metastabilen Systems jedoch bei einem Kohlenstoffgehalt von 6,67 %, da das Gefüge dabei zu 100 % aus Zementit besteht. Chemisch gesehen setzt sich der Zementit aus drei Eisenatomen (mit je einer Atommasse von 56 u) und einem Kohlenstoffatom (mit einer Atommasse von 12 u) zusammen. Somit ergibt sich der massenbezogene Kohlenstoffgehalt im Zementit zu 6,67 %:
\begin{align}
&\underline{\text{Kohlenstoffgehalt}} = \frac{12u}{12u+3 \cdot 56u} \cdot 100 \text{ %} = \underline{6,67 \text{ %}} \\[5px]
\end{align}
Bestimmung der Gefügeanteile und Phasenanteile
Grundsätzlich erfolgt die Bestimmung der Gefüge- und Phasenanteile durch Anwendung des Hebelgesetzes. Dabei müssen die Hebelarme immer bis an die entsprechenden Gefüge- bzw. Phasengrenzen gezogen werden. Im Folgenden sollen exemplarisch für einen über- und untereutektoiden Stahl die Gefüge- und Phasenanteile bei Raumtemperatur ermittelt werden.
Untereutektoide Stähle
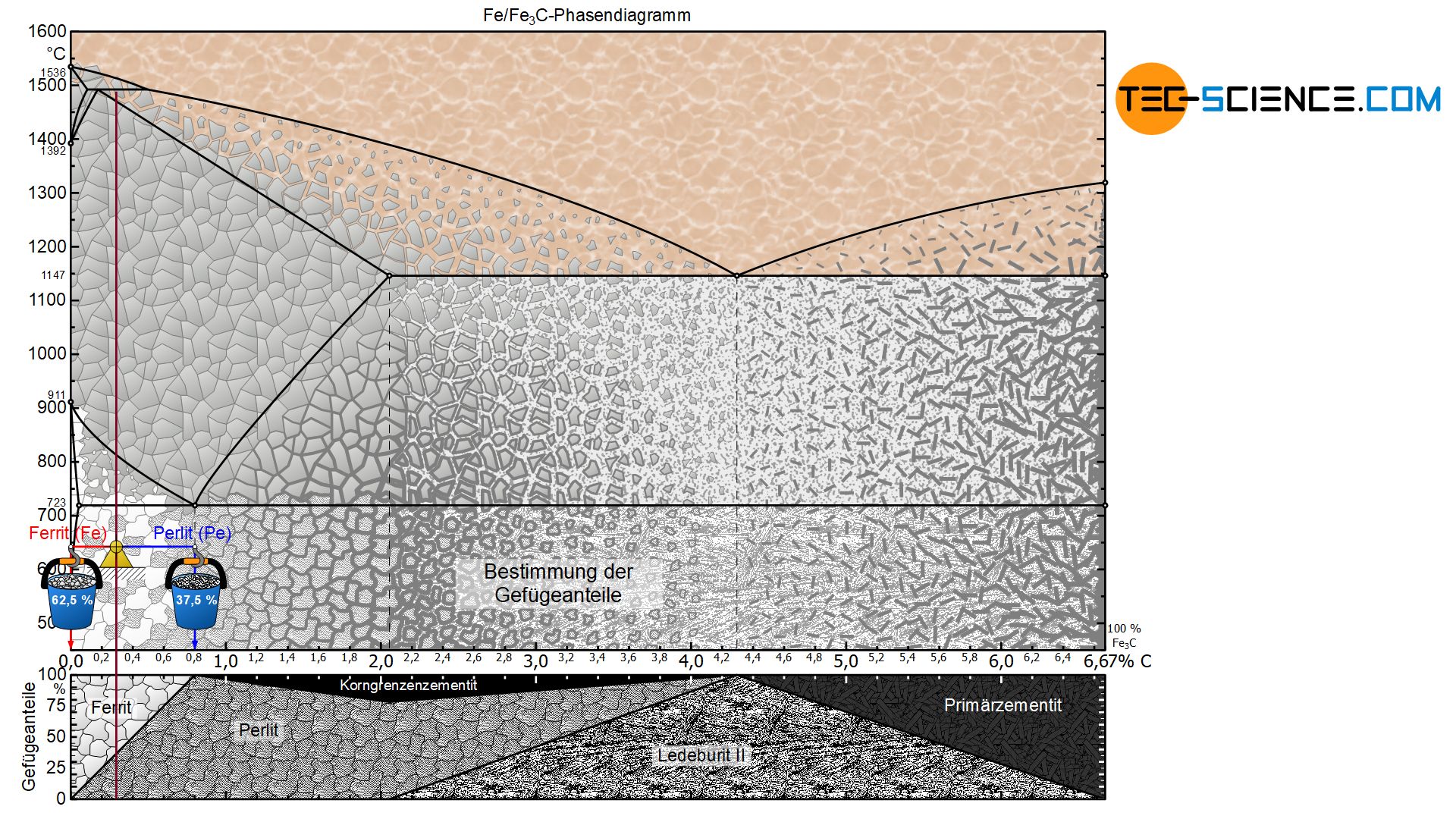
Bei einem untereutektoiden (unterperlitischen) Stahl besteht das Gefüge bei Raumtemperatur aus Ferrit- und Perlitkörner. Um die jeweiligen Gefügeanteile zu bestimmen, werden die Hebelarme ausgehend des betrachteten Zustandspunktes entsprechend bis hin zum Ferritgebiet (bei 0 % Kohlenstoff) und zur Perlitgrenze (bei 0,8 % Kohlenstoff) gezogen.
Für einen Stahl mit bspw. 0,3 % Kohlenstoff ergibt sich somit bei Raumtemperatur ein Ferritanteil von 62,5 % und entsprechend einen Perlitanteil von 37,5 %:
\begin{align}
&\underline{\text{Ferrit}} = \frac{0,8-0,3}{0,8} \cdot 100 \text{ %} = \underline{62,5 \text{ %}} \\[5px]
&\underline{\text{Perlit}} = \frac{0,3}{0,8} \cdot 100 \text{ %} = \underline{37,5 \text{ %}} \\[5px]
\end{align}
Aufgrund des Hebelgesetzes ergibt sich im Allgemeinen ein linearer Zusammenhang zwischen dem Kohlenstoffgehalt und den Gefügeanteilen. Für einen untereutektoiden Stahl steigt der Perlitanteil mit größerem Kohlenstoffgehalt stetig, bis dieser bei 0,8 % Kohlenstoff schließlich 100 % beträgt. Entsprechend nimmt der Ferritanteil bis auf 0 % ab. Der explizite Zusammenhang ist unterhalb des Phasendiagramms in einem Gefügediagramm abgebildet.
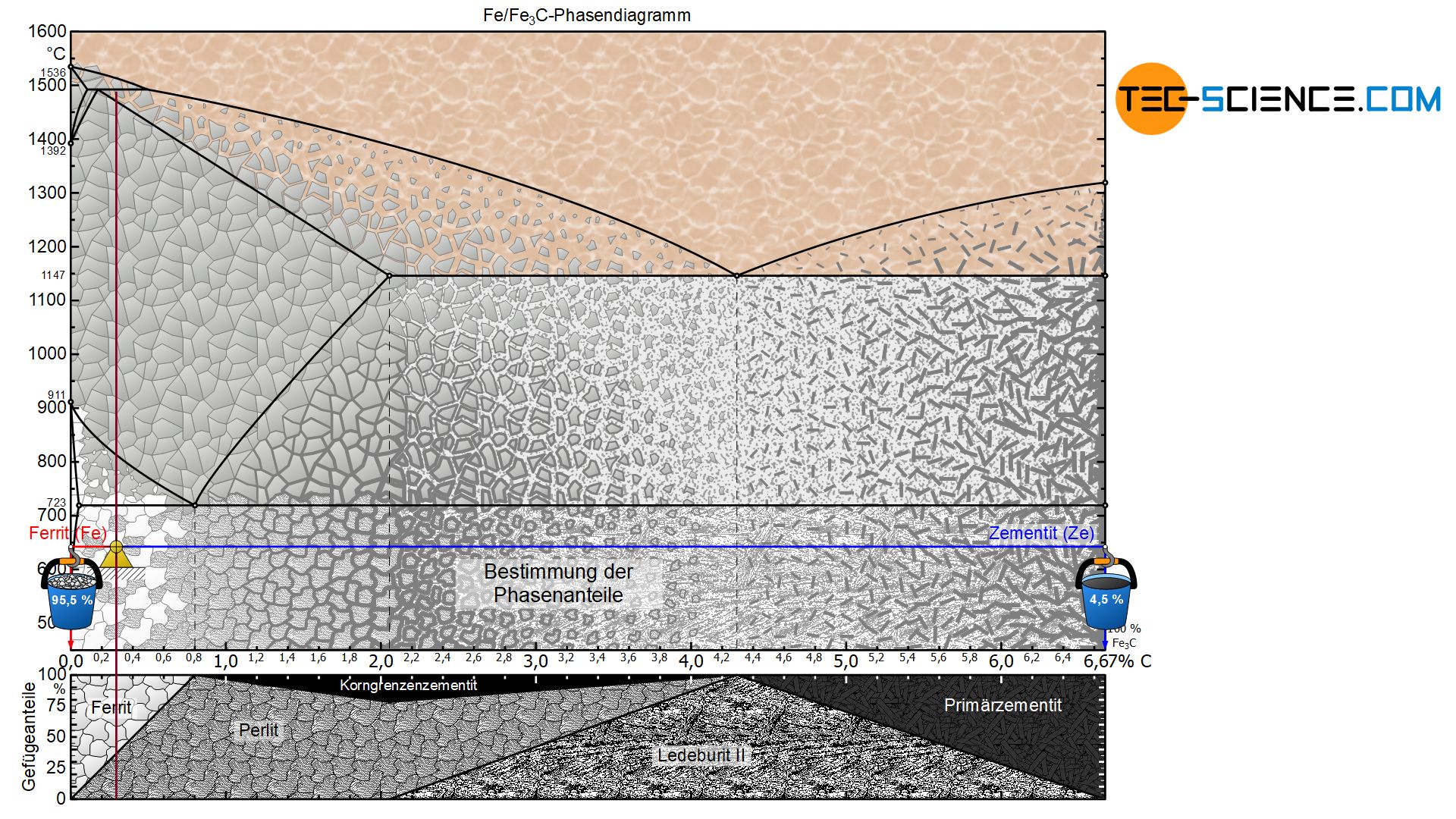
Der Begriff Gefügeanteil („Körneranteil“) darf an dieser Stelle nicht mit dem Begriff des Phasenanteils verwechselt werden! Denn schließlich besteht der Gefügebestandteil Perlit aus einem Phasengemisch, das sich sowohl aus Ferrit als auch aus Zementit zusammensetzt. Der Stahl lässt sich somit auch durch die Phasenanteile Ferrit und Zementit, statt durch die Gefügebestandteile Ferrit und Perlit charakterisieren. Die Vorgehensweise zur Bestimmung der Phasenanteile ist zwar grundsätzlich identisch, es muss jedoch beachtet werden, dass die Hebelarme dann allerdings bis zu den jeweiligen Phasengrenzen Ferrit und Zementit gezogen werden müssen.
Für den untereutektoiden Stahl mit 0,3 % Kohlenstoff bestimmt sich der Phasenanteil an Ferrit somit zu insgesamt 95,5 %. Die restlichen 4,5 % entfallen schließlich auf die Phase Zementit:
\begin{align}
&\underline{\text{Ferrit}} = \frac{6,67-0,3}{6,67} \cdot 100 \text{ %} = \underline{95,5 \text{ %}} \\[5px]
&\underline{\text{Zementit}} = \frac{0,3}{6,67} \cdot 100 \text{ %} = \underline{4,5 \text{ %}} \\[5px]
\end{align}
Übereutektoide Stähle
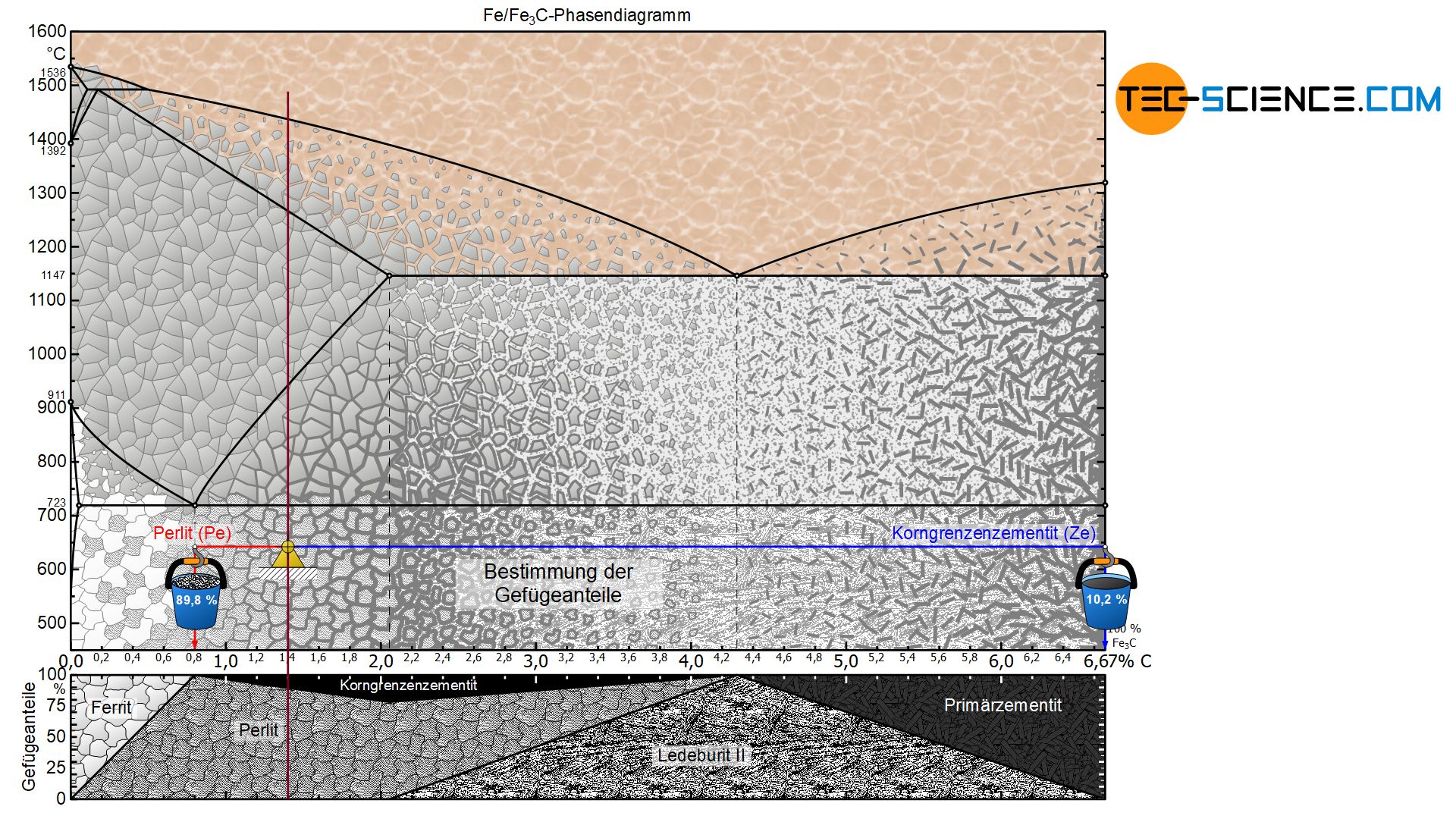
Auf die analoge Weise wie bei untereutektoiden Stählen können die Gefügebestandteile bei übereutektoiden Stählen bestimmt werden. Hierzu werden die Hebelarme bis an die jeweiligen Gefügebestandteile des Perlits (bei 0,8 % Kohlenstoff) und des Korngrenzenzementits (bei 6,67 % Kohlenstoff) gezogen.
Für einen Stahl mit bspw. 1,4 % Kohlenstoff ergibt sich somit bei Raumtemperatur ein Perlitanteil von rund 89,8 % und entsprechend einen Korngrenzenzementitanteil von 10,2 %:
\begin{align}
&\underline{\text{Perlit}} = \frac{6,67-1,4}{6,67-0,8} \cdot 100 \text{ %} = \underline{89,8 \text{ %}} \\[5px]
&\underline{\text{Korngrenzenzementit}} = \frac{1,4-0,8}{6,67-0,8} \cdot 100 \text{ %} = \underline{10,2 \text{ %}} \\[5px]
\end{align}
Grundsätzlich sinkt für einen übereutektoiden Stahl der Perlitanteil mit steigendem Kohlenstoffgehalt stetig bis auf minimal 78,5 % (bei 2,06 % Kohlenstoff). Entsprechend steigt der Anteil an Korngrenzenzementit bis auf maximal 21,5 %. Der detailliertere Zusammenhang zeigt das entsprechende Gefügediagramm unterhalb des Eisen-Kohlenstoff-Diagramms.
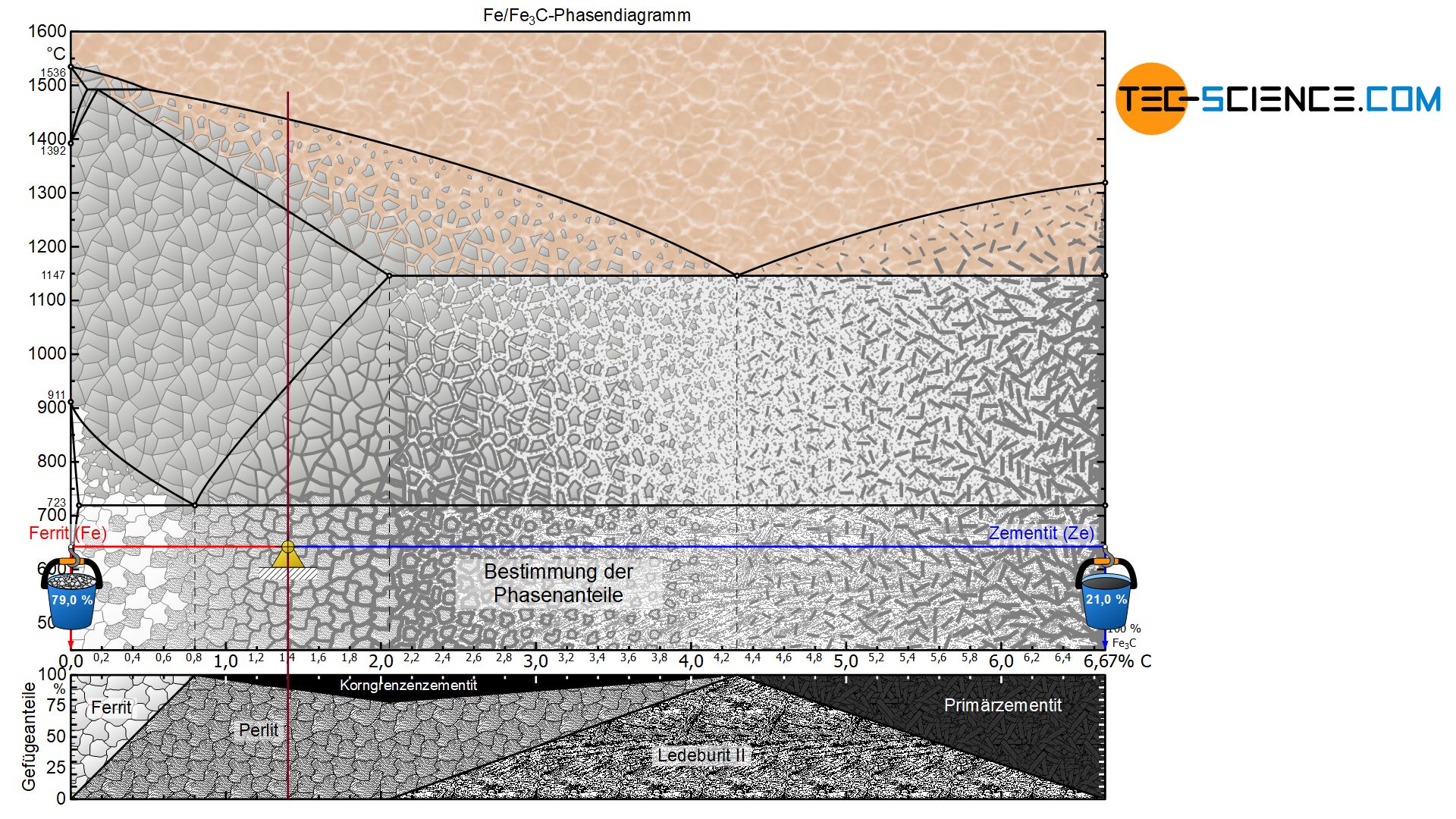
Auch für einen übereutektoiden Stahl ist der Begriff des Gefügeanteils wieder von dem Begriff des Phasenanteils zu unterscheiden. Schließlich befindet sich die Phase Zementit nicht nur an den Korngrenzen sondern auch im Perlitgefüge, welches zudem noch aus Ferrit besteht. Die entsprechenden Phasenanteile an Ferrit und Zementit können nach Ziehen der Hebelarme an die jeweiligen Phasengrenzen ermittelt werden.
Für den übereutektoiden Stahl mit 1,4 % Kohlenstoff bestimmt sich der Phasenanteil an Ferrit somit zu insgesamt 79,0 %. Die restlichen 21,0 % entfallen schließlich auf die Phase Zementit:
\begin{align}
&\underline{\text{Ferrit}} = \frac{6,67-1,4}{6,67} \cdot 100 \text{ %} = \underline{79,0 \text{ %}} \\[5px]
&\underline{\text{Zementit}} = \frac{1,4}{6,67} \cdot 100 \text{ %} = \underline{21,0 \text{ %}} \\[5px]
\end{align}