Radiation pressure is caused by the transfer of momentum of photons when they collide with matter.
Introduction
When light hits an object, this radiation exerts a certain force on that object and, with respect to the surface, also a certain pressure. This pressure is referred to as radiation pressure.

In the particle model, it is relatively easy to understand how the pressure of radiation comes about. According to quantum mechanics, any propagating wave can also be imagined as a beam of particles (wave–particle duality). The individual light particles are then also called photons.
In quantum theory, photons are light particles that make up electromagnetic radiation!

Each photon carries both energy and a momentum. If the photons from the radiation hit an object with a certain energy, they exert an collision force on impact, analogous to tennis balls thrown against a wall.
The radiation pressure is also the reason why the tail of comets is always directed away from the sun. Under atmospheric conditions, the detached gas and dust particles of a comet would normally be slowed down by air resistance. The tail formed by the detached particles would therefore always form against the heading. In the vacuum of space, however, there is no air resistance. Only the radiation pressure of the sun acts (not to be confused with the solar wind). The photons of solar radiation “blow” the tail away from the sun.

In theory, radiation pressure can also be used as an alternative propulsion technology for space travels. With so-called solar sails, the power of radiation is used for propulsion in the same way as wind power for wind sails. The force of the radiation is relatively low, but due to the lack of air friction in space this can lead to an enormous speed over a longer period of time. This technology is therefore particularly suitable for small probes and satellites that travel very long distances between planets. Such a solar-sail propulsion is currently still the subject of research.

Derivation
Energy of photons
The force that the photons exert on an impact with a surface area \(\Delta A\) depends on the momentum of the photons. The momentum can be calculated from the energy of the photons. The energy of a photon \(W_p\) in turn results from the frequency of the radiation \(f\) or its wavelength \(\lambda\):
\begin{align}
\label{w}
&W_p = h \cdot f = h \cdot \frac{\lambda}{c} \\[5px]
\end{align}
\(h\) refers to Planck’ constant and \(c\) to the speed at which electromagnetic radiation propagates (speed of light).
Momentum of photons
By the definition of the momentum as the product of mass and velocity (\(p=m v\)) and the famous mass-energy equivalence equation of Einstein (\(E=m c^2\)), a relationship between momentum and energy for photons can be derived.
The energy \(E\) in Einstein’s equation denotes the energy \(W_p\) of a photon and the velocity \(v\) in the formula for the momentum, denotes the speed of light of the photon \(c\) (\(m\) in this case stands for the relativistic mass of the photon).
\begin{align}
p &=m \cdot c &&~~~~~\text{momentum of photons}\\[5px]
W_p &=m \cdot c^2 &&~~~~~\text{mass-energy equivalence for photons}\\[5px]
\end{align}
If one divides the upper equations, then the following relationship results between momentum and energy of a photon:
\begin{align}
&\frac{p}{W_p}=\frac{m \cdot c}{m \cdot c^2} = \frac{1}{c} \\[5px]
& p = \frac{W_p}{c} \\[5px]
\end{align}
The same equation can also be derived using the energy-momentum relation from the theory of relativity:
\begin{align}
&W_p = \sqrt{(p \cdot c)^2+ (m_0 \cdot c)^2} ~~~~~\text{energy-momentum relation}\\[5px]
\end{align}
Since photons move at the speed of light and thus obviously cannot have a rest mass (\(m_0\)= 0), there is a relatively simple relationship between energy and momentum for photons:
\begin{align}
&W_p = p \cdot c \\[5px]
& p = \frac{W_p}{c} \\[5px]
\end{align}
Radiation pressure with complete absorption
In the following, the formula for calculating the radiation pressure is derived. It is assumed that the object completely absorbs the incident radiation.

If a total of \(\Delta N\) photons from the radiation hit a surface area \(\Delta A\) within a certain time \(\Delta t\), then the following total momentum \(p_{tot}\) results:
\begin{align}
&p_{tot} = p \cdot \Delta N = \frac{W_p}{c} \cdot \Delta N = W_p \cdot \Delta N \cdot \frac{1}{c} \\[5px]
\end{align}

At this point it can be used that the product of photon energy \(W_p\) and number of photons \(\Delta N\) corresponds to the amount of energy \(\Delta W\) that hits the area \(\Delta A\) within the time \(\Delta t\):
\begin{align}
&p_{tot} = \overbrace{W_p \cdot \Delta N }^{=\Delta W} \cdot \frac{1}{c} =\Delta W \cdot \frac{1}{c} \\[5px]
\end{align}
Due to the law of conservation of momentum, this total momentum remains completely conserved even after the impact on the initially stationary object. If it is assumed that all photons are absorbed on impact, then this total momentum must be transferred completely to the object. From the change in momentum of the object \(\Delta p\) (impuls), which therefore corresponds to the total momentum \(p_{tot}\) of the particles, the exerted force \(F_{tot}\) on the object can be determined as momentum change per unit time:
\begin{align}
&F_{tot} = \frac{\Delta p}{\Delta t} = \frac{p_{tot}}{\Delta t} = \frac{\Delta W \cdot \frac{1}{c}}{\Delta t} = \frac{\Delta W}{\Delta t} \cdot \frac{1}{c} \\[5px]
\end{align}
In this equation, the quotient of energy and time can be interpreted as the radiant power \(\Phi_{beam}\) of the beam, i.e. as the amount of energy that hits the surface \(\Delta A\) per unit time:
\begin{align}
&F_{tot} = \overbrace{\frac{\Delta W}{\Delta t}}^{\Phi_{beam}} \cdot \frac{1}{c} = \Phi_{beam} \cdot \frac{1}{c} \\[5px]
\end{align}
Since the force \(F_{tot}\) acts on the surface \(\Delta A\), it is now possible to calculate the pressure caused by the incident particle beam with the power \(\Phi_{beam}\). This pressure is also called radiation pressure \(p_{beam}\) (not to be confused with the photon momentum \(p\)!):
\begin{align}
\label{ww}
&p_{beam} = \frac{F_{tot}}{\Delta A} =\frac{\Phi_{beam}}{\Delta A} \cdot \frac{1}{c} \\[5px]
\end{align}
The quotient of the incident radiant power \(\Phi_{beam}\) and the respective surface area \(\Delta A\) is also called intensity or irradiance or radiant flux density, since this quantity is a measure of how strongly an area is irradiated with energy (surface power density). There is therefore a relatively simple relationship between intensity \(I\) and radiation pressure:
\begin{align}
&\boxed{p_{beam} =\frac{I}{c}} ~~~~~\text{only valid for complete absorption} \\[5px]
\end{align}
Intensity or irradiance is the term used to describe the area-related radiant power (surface power density)!
Radiation pressure with complete reflection
Note that the above relationship between radiation pressure and intensity only applies if the radiation is completely absorbed when it hits the object!
If, on the other hand, the radiation is completely reflected, then the photons are returned with the same magnitude of momentum, but in the reflected direction. In order for the total momentum to be conserved, the object had to be subjected to an impulse change twice as large. Accordingly, a radiation pressure twice as high acts on the reflecting object at the same intensity!
\begin{align}
&\boxed{p_{beam} =2 \frac{I}{c}} ~~~~~\text{only valid for complete reflection} \\[5px]
\end{align}
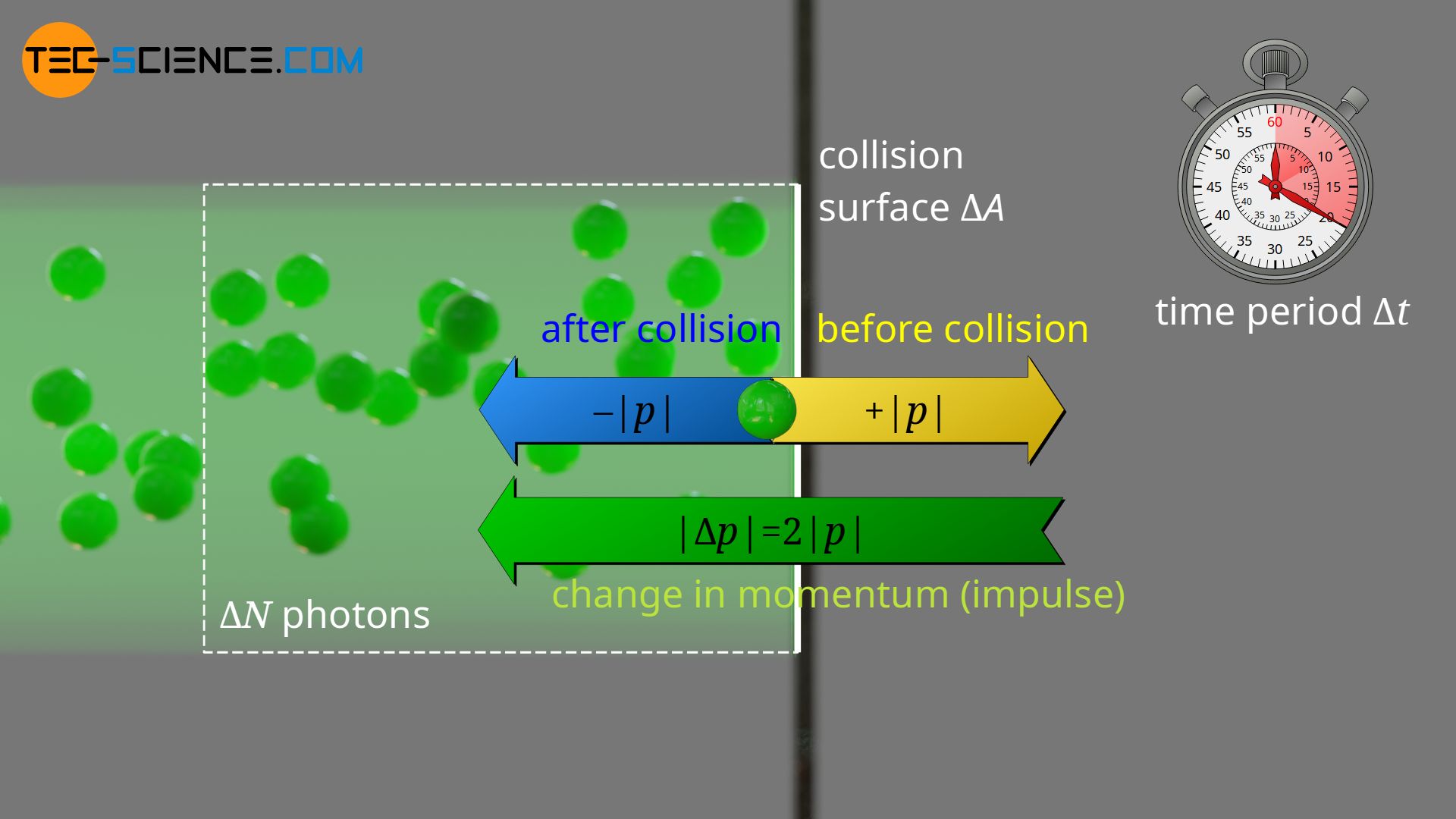
The radiation pressure on an ideally reflecting surface is twice as large as on an ideally absorbing surface!
The fact that the radiation pressure with reflection is twice as high as with absorption can also be clearly understood. An analogous example is a person standing on a frictionless skateboard. If a heavy medicine ball is thrown at this person, the momentum is transferred to the person including the skateboard when the ball is caught. This catching of the ball corresponds in the figurative sense to the complete absorption of the photons.
But not only by throwing and catching the ball can the person be set in motion, but also by throwing it away. When throwing the ball away, the person pushes himself away from the medicine ball and also gets an impulse (“rocket principle”).
So if the person gets a medicine ball thrown at him and then throws it away again, then he has used it in two ways. Not only does he get an impulse by catching it, but he also generates an impulse by throwing it away. If the ball is thrown off again with the same (relative) speed as it was caught, then the person has been able to transfer the double impulse to himself (double force) compared to the pure “absorbing” of the ball.
If one makes the catching and throwing of the ball faster and faster in thought, then it is kinematically regarded as a pure rebound of the ball at the person, i.e. a reflection! A reflection thus produces an impulse twice as large as an absorption.
Relationship between radiation pressure and energy density
Directed radiation (photon beam)
At this point equation (\ref{w}) shall be interpreted in another respect. If the propagation speed of the wave \(c\) (speed of light) is expressed by the distance travelled (\Delta s) within the time \(\Delta t\), then we obtain:
\begin{align}
&p_{beam} = \frac{\Phi_{beam}}{\Delta A} \cdot \frac{1}{c} = \frac{\Phi_{beam}}{\Delta A} \cdot \frac{1}{\frac{\Delta s}{\Delta t}} = \frac{\overbrace{\Phi_{beam}\cdot \Delta t}^{\Delta W}}{\underbrace{\Delta A \cdot \Delta s}_{\Delta V}} =\frac{\Delta W}{\Delta V} = w \\[5px]
&\boxed{p_{beam} = w} ~~~~~\text{only valid with complete absorption}
\end{align}

In the equation above, it was used that the product of radiant power and time corresponds to the energy of the radiation \(\Delta W\) contained in the volume \(\Delta V\) and which then exerts the radiation pressure \(p_{beam}\). The quotient of radiant energy and volume is also called energy density \(w\) and represents the radiant energy per unit volume.
As this equation states, the radiation pressure can also be understood as energy density! This direct correlation between volumetric energy density and radiation pressure is only valid if the radiation is completely absorbed when it hits the object!
In this case, the radiation must also hit the absorbing surface perpendicularly. For example, if the surface is parallel to the radiation, then the photons obviously do not collide with the surface. Consequently, no radiation pressure is exerted, although the radiation of course still has an energy and thus an energy density (the energy does not hit the surface, so to speak).
The energy density of a directed beam of radiation corresponds with complete absorption to the radiation pressure!
In contrast to the case of complete absorption, with complete reflection of the radiation the same energy density leads to a radiation pressure twice as high, since the impulse is twice as high:
\begin{align}
&\boxed{p_{beam} = 2w} ~~~~~\text{only valid with complete reflection}
\end{align}
Non-directed radiation (photon gas)
Note that the derived correlations between radiation pressure and energy density are only valid for directional radiation. In these cases, all photons move in the same direction. Thus also all photons take part in the exercise of the pressure.
The situation is different when it is no longer a matter of directional radiation but of a completely statistical distribution of photon motion. This is the case, for example, when radiation is observed in a mirrored cavity.

The photons are then permanently reflected on the walls and over time a completely random photon movement will form. From the originally directed motion, in which all particles moved towards the wall, on average only one sixth will now be moving in the direction of the wall. The remaining particles will move to the right, to the left, upwards, downwards or away from the wall. At the same energy density (photon density), the radiation pressure at such a random photon motion is only one sixth compared to a directed photon beam:
\begin{align}
&\boxed{p= \frac{1}{6} \cdot p_{beam} = \frac{1}{6}\cdot 2w = \frac{1}{3}w} ~~~~~\text{applies only to non-directed radiation}
\end{align}

The chaotic motion of photons is similar to the motion of particles in gases. For this reason, this type of disordered radiation is also called photon gas. The Stefan-Boltzmann law for radiating bodies, for example, can be derived by looking at radiation as a photon gas and the relationship between energy density and radiation pressure.


