Erfahre in diesem Artikel mehr über die Konstruktion der Kurvenscheibe eines Zykloidgetriebes.
Form der Kurvenscheibe
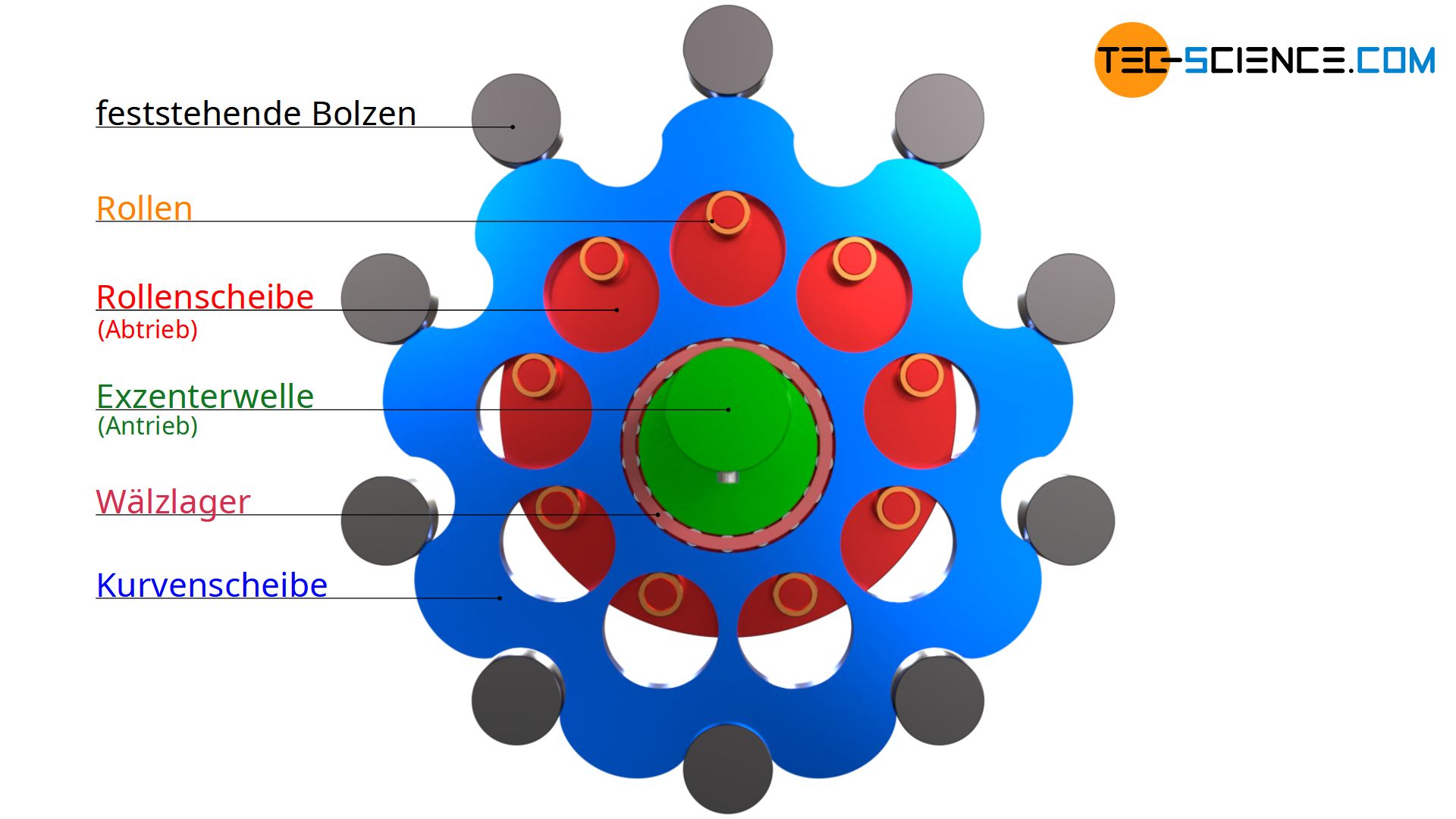
Kurvenscheiben mit gewöhnlicher Zykloide
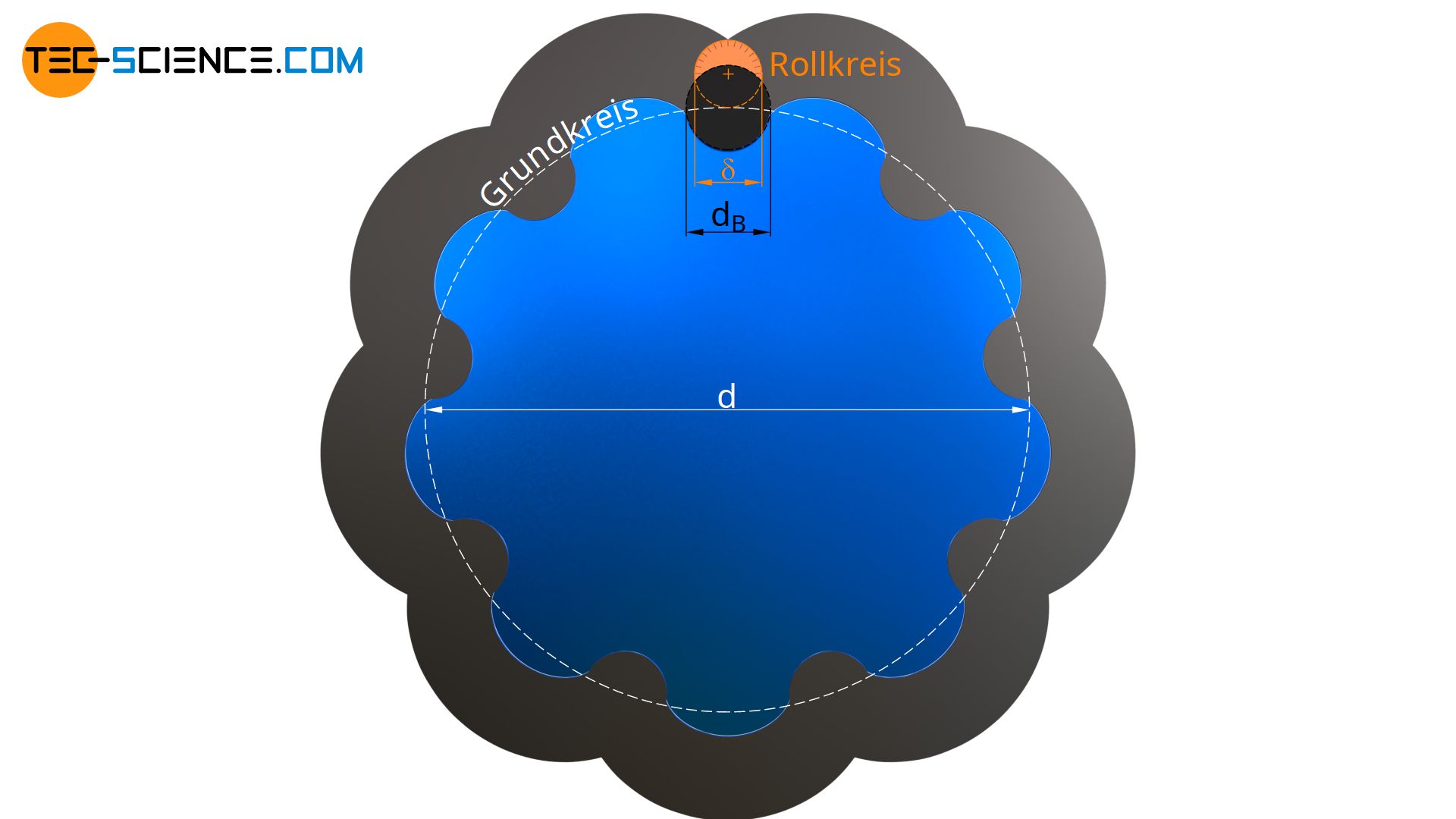
Wie bereits im Artikel „Funktionsweise“ erwähnt, setzt sich die Grundform der Kurvenscheibe eines Zykloidgetriebes aus einer Zykloide zusammen. Eine solche Zykloidenform erhält man, wenn man einen Rollkreis auf einem Grundkreis abrollt (siehe auch Artikel „Geometrie von Zykloidenzahnräder„). Ein Punkt am Umfang des Rollkreises beschreibt als Bahnkurve dabei die Zykloide. Die erhaltene Kurve bildet das sogenannte Bezugsprofil oder auch Nennprofil genannt.
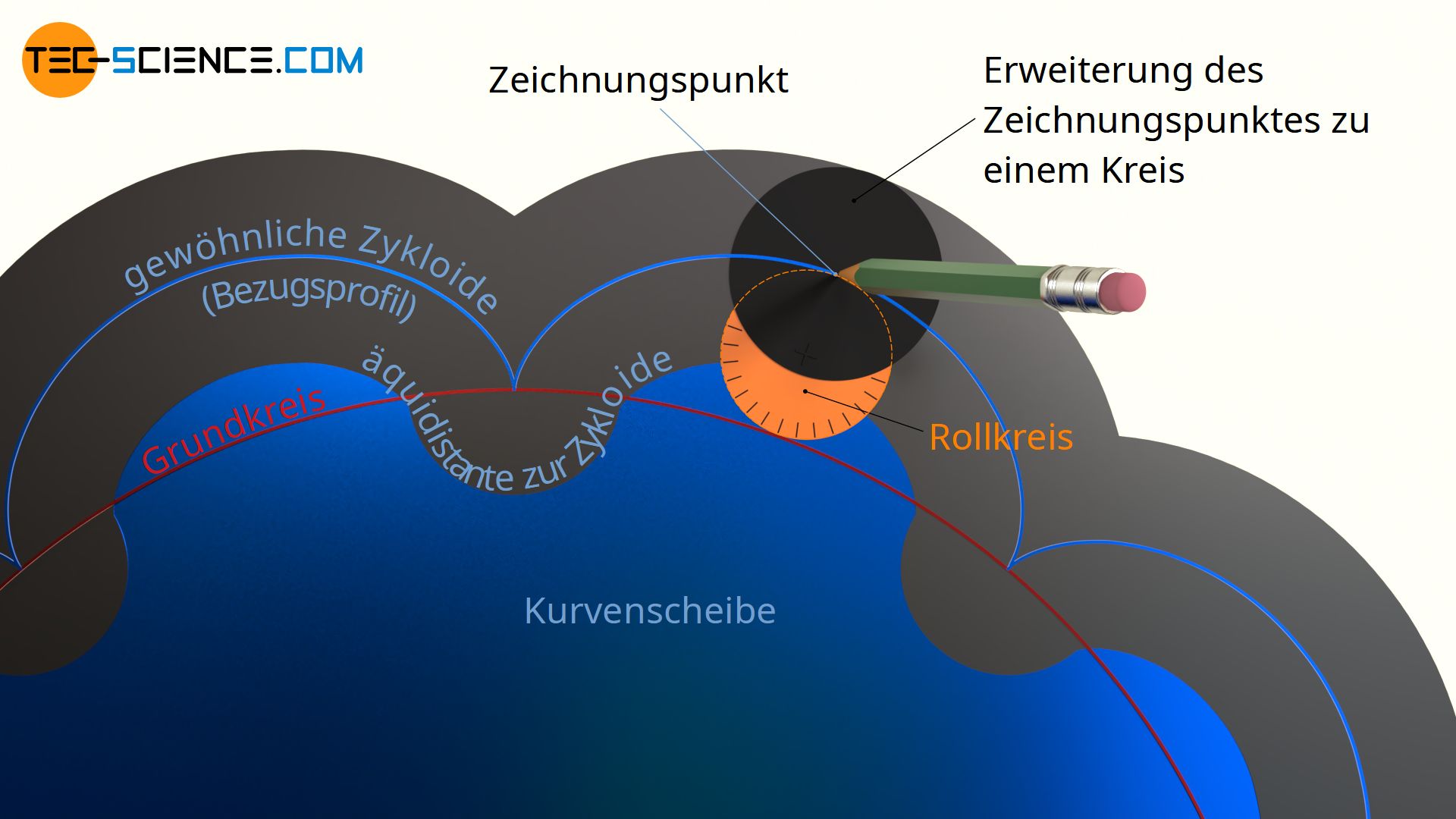
Nun muss jedoch beachtet werden, dass sich die Kurvenscheibe später um die Bolzen wälzen muss. Aus diesem Grund muss bei der Konstruktion der Zykloide der Zeichnungspunkt („Bleistiftspitze“) zu einem Kreis erweitert werden, wobei der Durchmesser dieses Zeichnungskreises dem Bolzendurchmesser entspricht, um die sich die Kurvenscheibe später wälzt! Die einhüllende Kontur die nun beim Abrollen des Rollkreises mit seinem Zeichnungskreis entsteht entspricht dann dem eigentlichen Profil der Kurvenscheibe.
Ein solches Scheibenprofil kann man sich auch wie folgt konstruiert vorstellen. Zunächst wird das Bezugsprofil wie üblich mit einem Zeichnungspunkt hergestellt. Anschließend setzt man nun in Gedanken den Mittelpunkt eines Fräsers (dessen Durchmesser dem späteren Bolzendurchmesser entspricht) auf dieses Bezugsprofil und fräst entlang der Zykloide. Auch auf diese Weise erhält man dann aus dem Bezugsprofil das eigentliche (äquidistante) Scheibenprofil.
Das Profil der Kurvenscheibe wird aus einer äquidistanten Linie zur Zykloide erhalten!
Kurvenscheiben mit verkürzter Zykloide
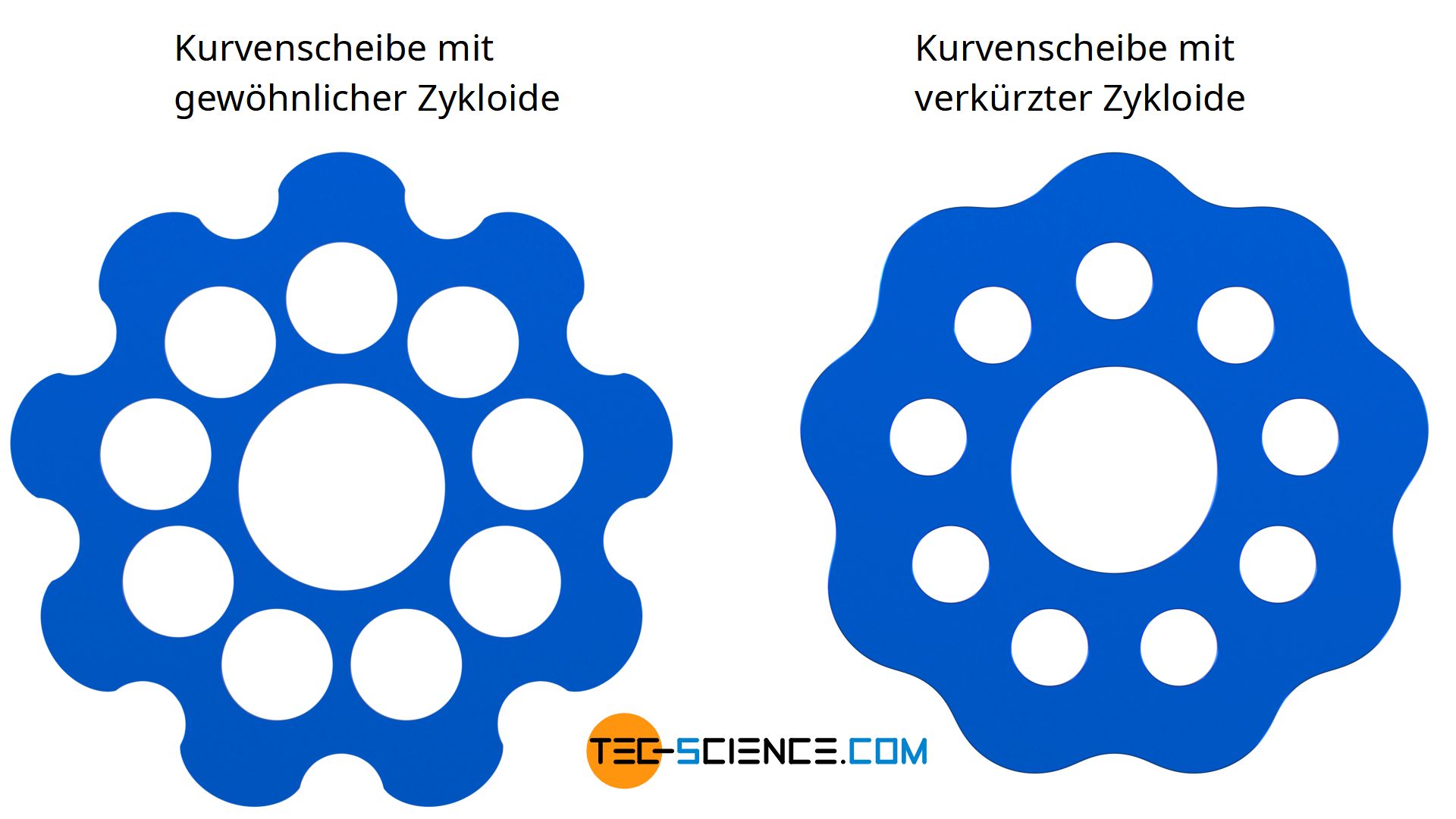
Die im Abschnitt zuvor konstruierte Kurvenscheibe besitzt eine relativ große Exzentrizität, was bei großen Drehzahlen zu enormen Unwuchtkräften führt und einen entsprechend unruhigen Lauf zur Folgen hat. Mit dieser relativ großen Exzentrizität hängt es auch zusammen, dass die Löcher der Zykloidenscheibe relativ nahe beieinander liegen. Die geringe Materialstärke zwischen den Löchern könnte bei großen Kräften somit zu einer Verformung der Löcher führen.
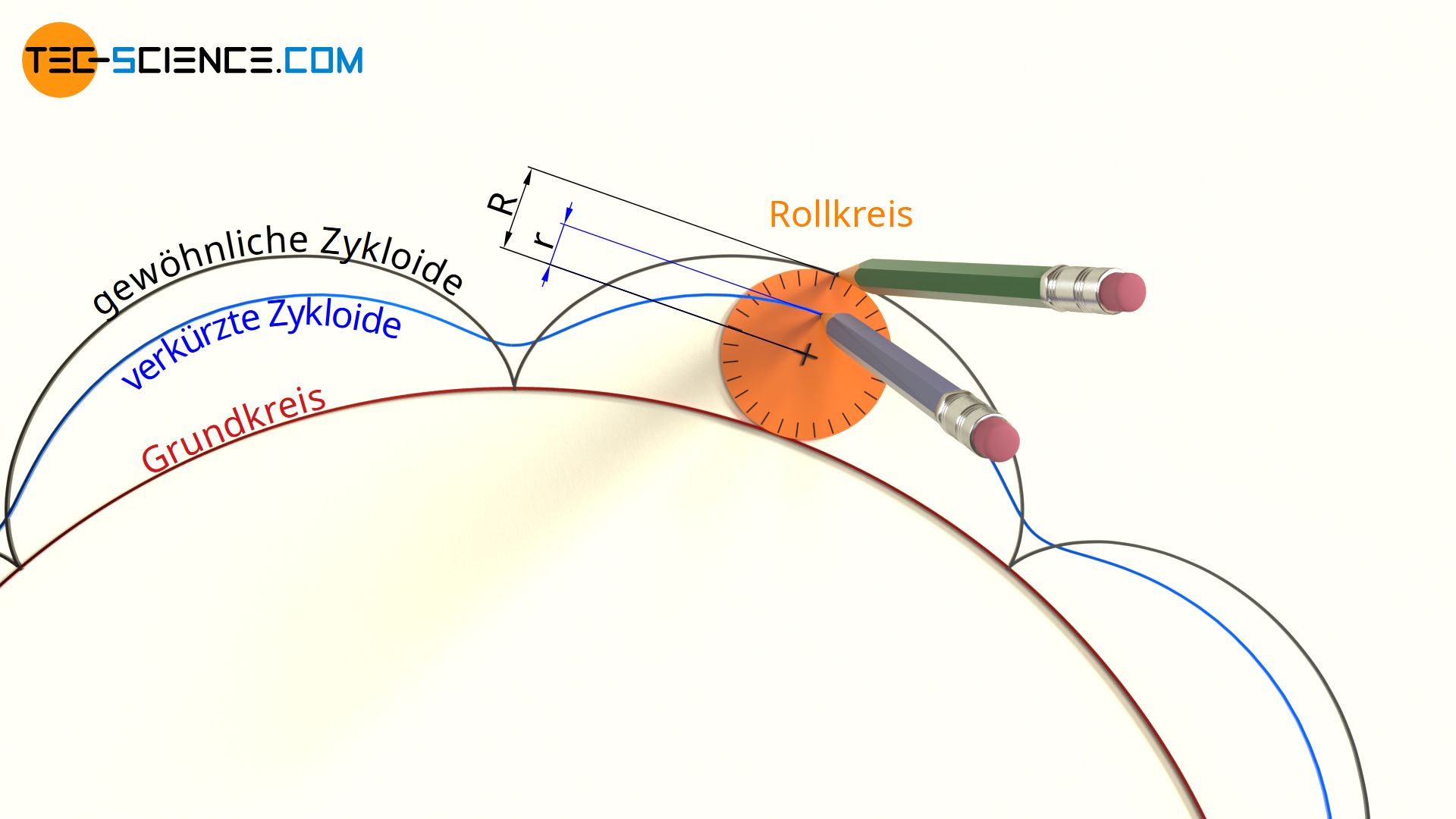
Aus diesen Gründen wird die Kurvenscheibe häufig mit einer sogenannten verkürzten Zykloide konstruiert. Dabei wird letztlich der Zeichnungspunkt nicht mehr am Umfang des Rollkreises platziert (Abstand R) sondern befindet sich innerhalb des Rollkreises (Abstand r<R). Im Gegensatz hierzu spricht man von einer verlängerten Zykloide, wenn sich der Zeichnungspunkt außerhalb des Rollkreises befindet (r>R). Letztere hat jedoch im Maschinenbau keine Bedeutung, weshalb lediglich die verkürzte Zykloide zur Anwendung kommt.
Die untere Abbildung zeigt die Auswirkung einer solchen verkürzten Zykloide auf die Form der Kurvenscheibe. Die Kontur der Zykloidenscheibe verläuft im Vergleich zur Konstruktion mit einer gewöhnlichen Zykloide „weicher“. Sowohl die Exzentrizität als auch die späteren Lochdurchmesser in der Kurvenscheibe fallen deutlich geringer aus.
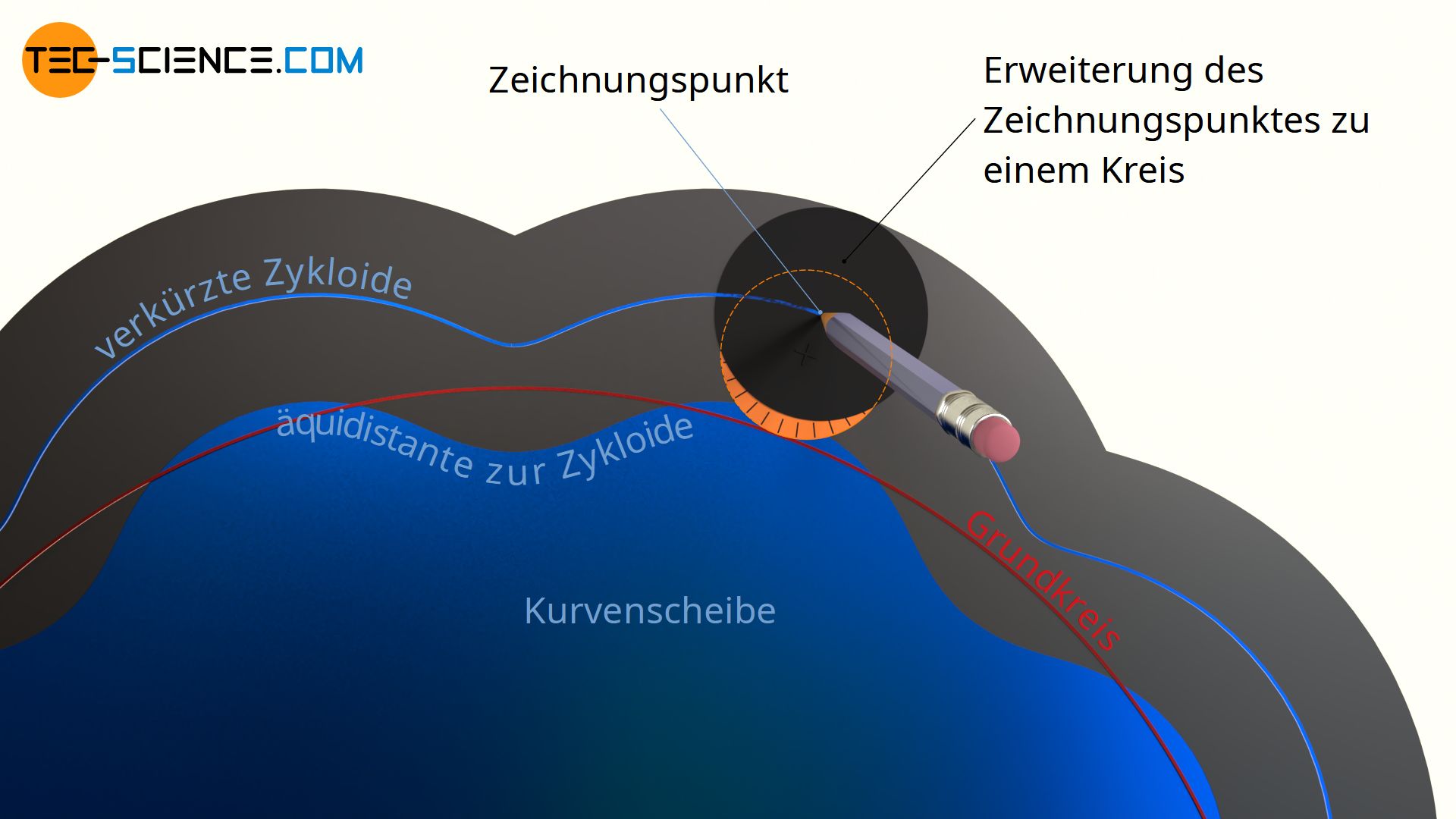
Die untere Animation zeigt hierzu das Getriebeverhalten der Kurvenscheibe mit verkürzter Zykloide.
Das Übersetzungsverhältnis ändert sich durch die Konstruktion mit verkürzter Zykloide im Übrigen nicht; dieses ist nur von der Anzahl der „Nocken“ (n) der Kurvenscheibe und der Anzahl der Bolzen (N) abhängig (mehr hierzu siehe Artikel „Funktionsweise„):
\begin{align}
&\boxed{i = \frac{n}{N-n} } \\[5px]
\end{align}
Das Übersetzungsverhältnis eines Zykloidgetriebes spiegelt sich schließlich im Verhältnis zwischen Grundkreisdurchmesser und Rollkreisdurchmesser wieder, welcher zur Konstruktion der Zykloidenscheibe verwendet wird. Denn aus der Betrachtung der Zykloidenscheibe heraus handelt es sich schließlich um ein Abwälzen der Bolzen auf der Zykloidenscheibe (auch wenn sich die Sicht als außenstehender Beobachter gerade umgekehrt zeigt: die Zykloidenscheibe wälzt auf den Bolzen ab – eben nur eine Frage der Sichtweise).
\begin{align}
\label{2}
&i=\frac{d}{\delta} \\[5px]
\end{align}
Konstruktion des Zykloidgetriebes
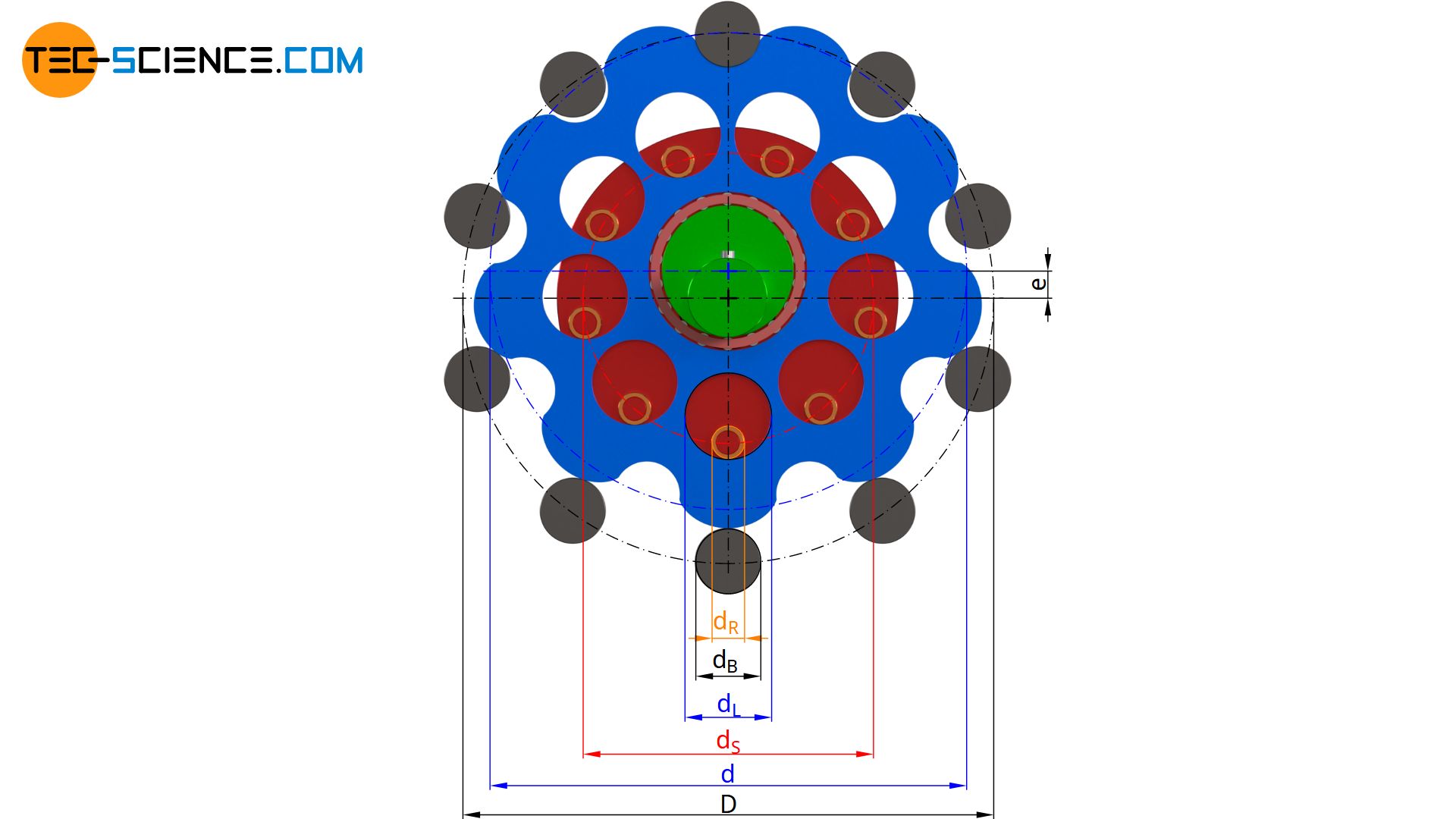
Anhand der oben gezeigten Zykloidenscheibe soll die Ermittlung der für die Konstruktion des Zykloidgetriebes erforderlichen Parameter gezeigt werden. Der Wälzkreis bzw. Teilkreis auf dem die Bolzen angeordnet werden ist im vorliegenden Fall mit D = 160 mm gewählt und die Bolzendurchmesser sollen dB = 20 mm betragen. Insgesamt werden N=10 Bolzen verwendet, die zu einem Übersetzungsverhältnis von i= 9 führen sollen. Die Rollen der Rollenscheibe haben einen gewählten Durchmesser von dR = 14 mm. Die Rollen selbst sind auf einem Teilkreis mit dem Durchmesser dS = 88 mm angeordnet. Die Exzentrizität der rotierenden Zykloidenscheibe soll e = 4 mm betragen.
Die oben genannten Parameter sind im Vorfeld prinzipiell frei wählbar, sollten jedoch sinnvoll gewählt werden. Mithilfe der unten nochmals zusammengefassten Größen kann die Kurvenscheibe nun konstruiert werden:
- Teilkreisdurchmesser D der ringförmig angeordneten Bolzen
- Bolzendurchmesser dB
- Anzahl N der Bolzen
- Übersetzungsverhältnis i
- Durchmesser dR der Rollen
- Teilkreisdurchmesser dS der Rollen auf der Rollenscheibe
- Exzentrizität e der Kurvenscheibe
Rollkreisdurchmesser
Der Rollkreisdurchmesser δ zur Konstruktion Zykloidenscheibenform muss zunächst so gewählt werden, dass der Rollkreisumfang gerade der Umfangsteilung der Bolzen auf der Gehäusescheibe entspricht. Nur so ist gewährleistet, dass der mit dem Rollkreis konstruierte Zahnabstand der Zykloidenscheibe den Bolzenabständen entspricht und ein späteres Ineinandergreifen ermöglicht wird. Da Durchmesser und „Zähnezahlen“ (Bolzenanzahl bzw. Anzahl der Nocken) proportional zueinander sind, muss der Rollkreisdurchmesser δ folglich um den Faktor der Bolzenanzahl N kleiner als der Teilkreisdurchmesser Dder Bolzen sein:
\begin{align}
\label{3}
&\boxed{\delta=\frac{D}{N}}~(= 16 \text{ mm}) \\[5px]
\end{align}
Damit ist in Kombination mit Gleichung (\ref{2}) nun auch der Grundkreisdurchmesser d (gleichbedeutend mit dem Wälzkreisdurchmesser) zur Konstruktion der Zykloidenscheibe eindeutig festgelegt:
\begin{align}
&i=\frac{d}{\delta}=\frac{d \cdot N}{D} \notag \\[5px]
\label{4}
&\boxed{d = \frac{i}{N} \cdot D} ~(= 144 \text{ mm}) \\[5px]
\end{align}
Exzentrizität
Der Abstand des Zeichnungspunktes zum Rollkreismittelpunkt während der Konstruktion der Kurvenscheibenform entspricht direkt der späteren Exzentrizität e der Zykloidenscheibe, denn dieser Abstand bestimmt letztlich die „Amplitude“ mit der der Zeichnungskreis während der Konstruktion der Zykloide um den Grundkreis „schwankt“. In der Praxis geht man jedoch den umgekehrten Weg: Die Exzentrizität wird bereits im Vorfeld festgelegt und entscheidet somit über die Form der Zykloidenscheibe. Dabei ist die Exzentrizität stets kleiner oder im Extremfall gleich dem halben Durchmesser des Rollkreises.
\begin{align}
&\boxed{e \le \frac{\delta}{2}} \\[5px]
\end{align}
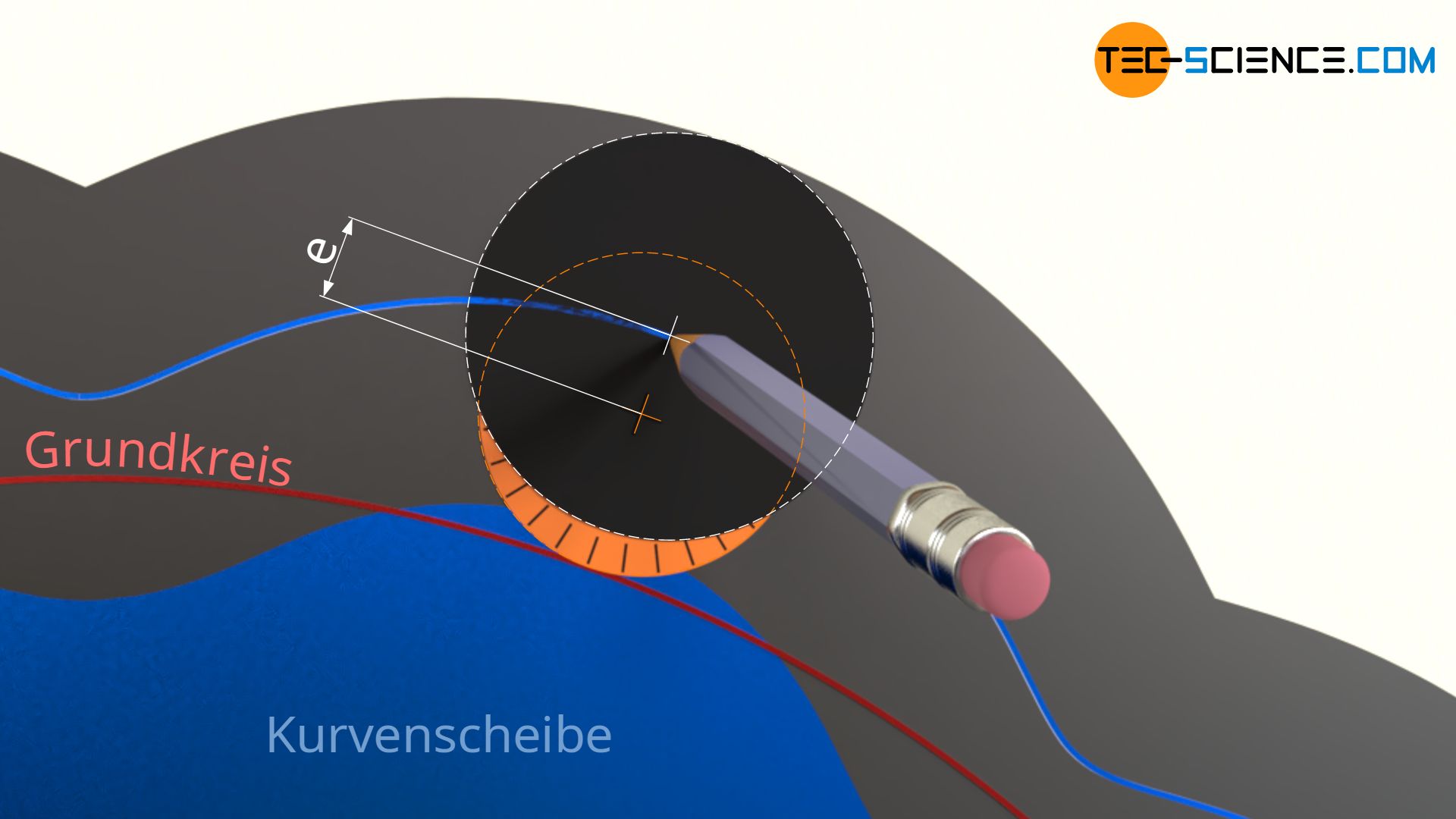
Im vorliegenden Beispiel ist die Exzentrizität bei der verkürzten Variante mit e = 4 mm gewählt worden. Zu gering sollte die Exzentrizität jedoch nicht gewählt werden, da die Kontur der Zykloidenscheibe sonst immer „weicher“ wird und im Extremfall bei einer Exzentrizität von e=0 in eine reine Kreisform übergeht. In diesem Fall ist natürlich kein Formschluss mehr möglich und auch bei zu geringen Exzentrizitäten besteht die Gefahr des „Drüberrutschens“ der Zykloidenscheibe über die Bolzen.
Lochdurchmesser der Kurvenscheibe
Die Exzentrizität e hat wiederum Einfluss auf die Lochdurchmesser dL der Zykloidenscheibe. Zum einen müssen durch die Löcher die Rollen mit ihrem Durchmesser dR passen und zum anderen müssen diese das „Schwanken“ der Zykloidenscheibe berücksichtigen, die sich bei einem Umlauf um die Exzentrizität „nach oben“ und „nach unten“ bewegt. Deshalb muss der Lochdurchmesser dL um den zweifachen Betrag der Exzentrizität e größer sein als der Rollendurchmesser dR:
\begin{align}
\label{exzenter}
&\boxed{d_L = d_R + 2 \cdot e} ~~~~(= 22 \text{ mm}) \\[5px]
\end{align}
Der Lochkreisdurchmesser auf dem die Löcher um das Zentrum der Zykloidenscheibe angeordnet werden entspricht dabei exakt dem Teilkreisdurchmesser auf dem die Rollen um das Zentrum der Rollenscheibe angeordnet sind (dS = 88 mm)!
Die Geometrie der Zykloidenscheibe bzw. des Zykloidgetriebes ist damit vollständig bestimmt!