Erfahre in diesem Artikel mehr über den Aufbau, die Funktionsweise sowie Vor- und Nachteile eines Zykloidgetriebes und dessen Anwendung.
Funktionsweise
Die untere Animation zeigt den Aufbau und das Funktionsprinzip eines Zykloidgetriebes.
Dabei treibt eine Exzenterwelle (Antriebswelle) zunächst eine Kurvenscheibe an. Ringförmig um die Exzenterwelle sind feststehende Bolzen angeordnet, in die die „Vertiefungen“ der Kurvenscheibe passen. Aufgrund der exzentrischen Bewegung wird die Kurvenscheibe um diese Bolzen getrieben, sodass die Kurvenscheibe um ihre Symmetrieachse rotiert. In der Kurvenscheibe sind Löcher angebracht, die im Gegensatz zur Exzenterwelle nun im Uhrzeigersinn rotieren. In diese Löcher greifen die Rollen einer dahinterliegenden Rollenscheibe. Die Kurvenscheibe treibt auf diese Weise die Rollenscheibe an, an der auch die zentrisch gelagerte Abtriebswelle angebracht ist und koaxial zur Antriebswelle sitzt.
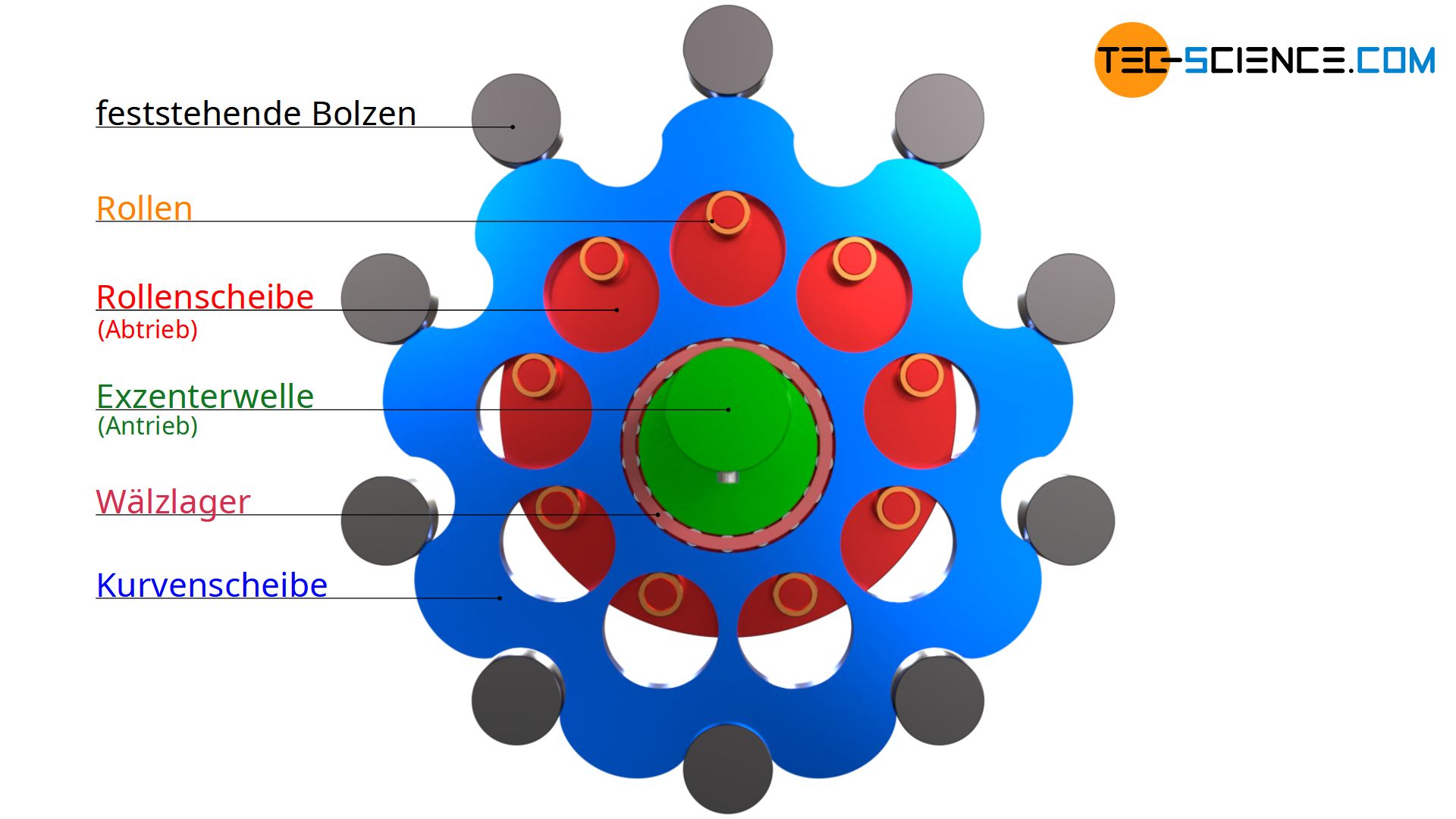
Vergleicht man in der oberen Animation die Drehzahl der Antriebswelle mit der Drehzahl Abtriebswelle, so tritt offenbar neben der Drehrichtungsumkehr eine Drehzahlreduzierung ein. In der vorliegenden Animation dreht sich die Rollenscheibe bei einer ganzen Umdrehung der Exzenterwelle (360°) um insgesamt 40° weiter. Erst nach 9 Umdrehungen der Antriebswelle hat die Abtriebswelle somit eine ganze Umdrehung hinter sich gebracht. Das Übersetzungsverhältnis des Getriebes beträgt damit 9:1.
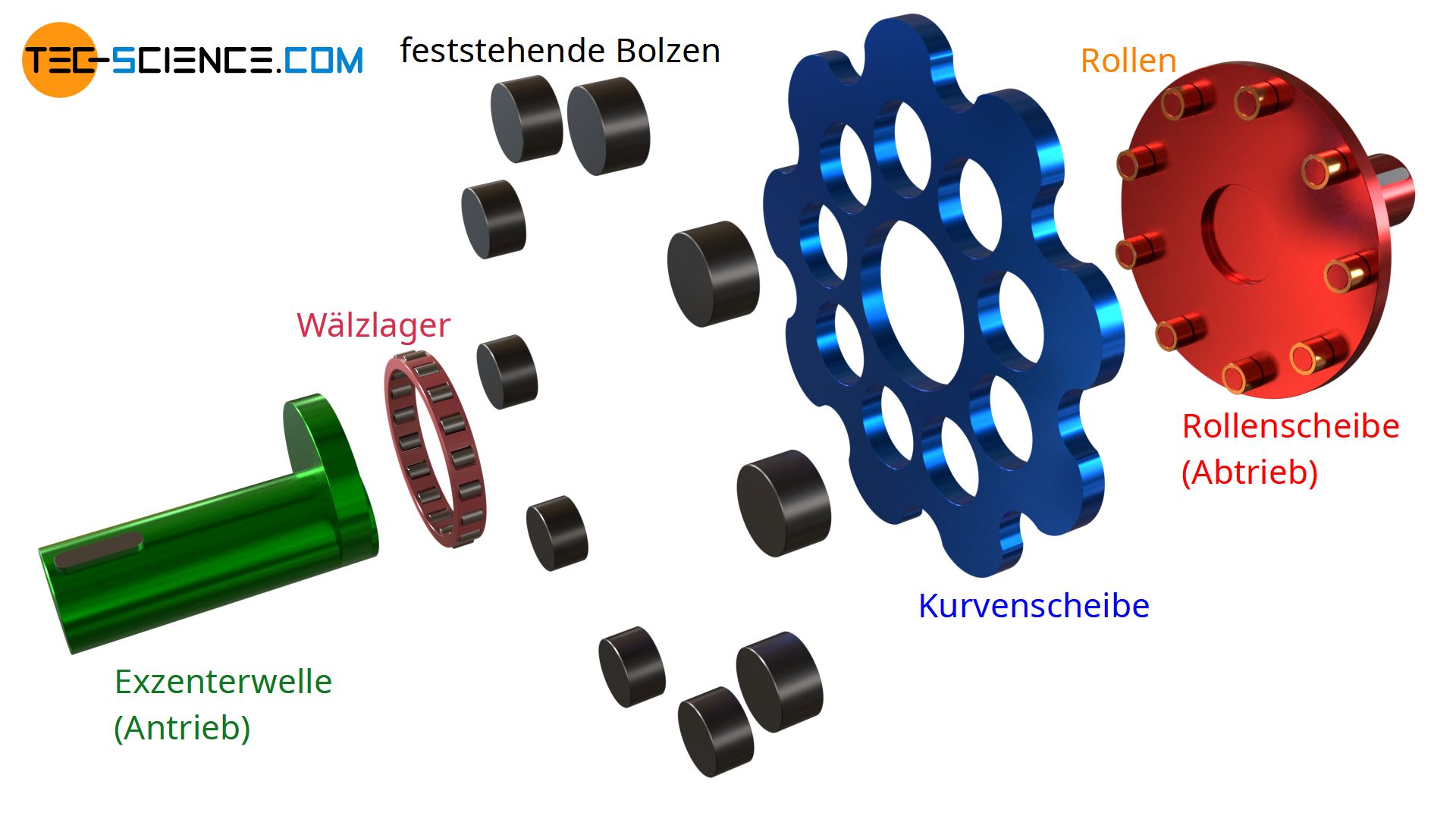
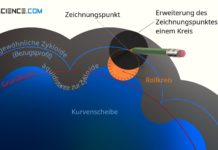
Herzstück des Zykloidgetriebes ist die Kurvenscheibe, dessen Geometrie für den Bewegungsablauf eine zentrale Rolle spielt. Die äußere Kontur der „Nocken“ und „Vertiefungen“ am Umfang der Kurvenscheibe lässt sich auf eine eine Zykloide zurückführen. Deshalb wird die Kurvenscheibe auch als Zykloidenscheibe bezeichnet und das gesamte Getriebe Zykloidgetriebe genannt. Auf die Konstruktion der Geometrie der Kurvenscheibe wird im Artikel „Konstruktion der Zykloidenscheibe“ näher eingegangen.
Aufgrund der symmetrischen Lastverteilung werden in der Praxis häufig zwei Zykloidenscheiben verwendet die dann um 180° versetzt angeordnet sind. Auf diese Weise wird erreicht, dass sich die Unwuchtskräfte bei hohen Drehzahlen gegenseitig ausgleichen, was einen ruhigeren Lauf zur Folge hat. Die doppelte Ausführung der Zykloidenscheiben ermöglicht zudem die Übertragung von sehr großen Drehmomenten. Zudem werden die Zykloidenscheiben häufig mit einer sogenannten verkürzten Zykloide konstruiert, was eine „weichere“ Kontur mit verringerter Exzentrität zur Folge hat und zu kleineren Lochdurchmessern in der Zykloidenscheibe führt (mehr hierzu im Artikel „Konstruktion der Zykloidenscheibe„).
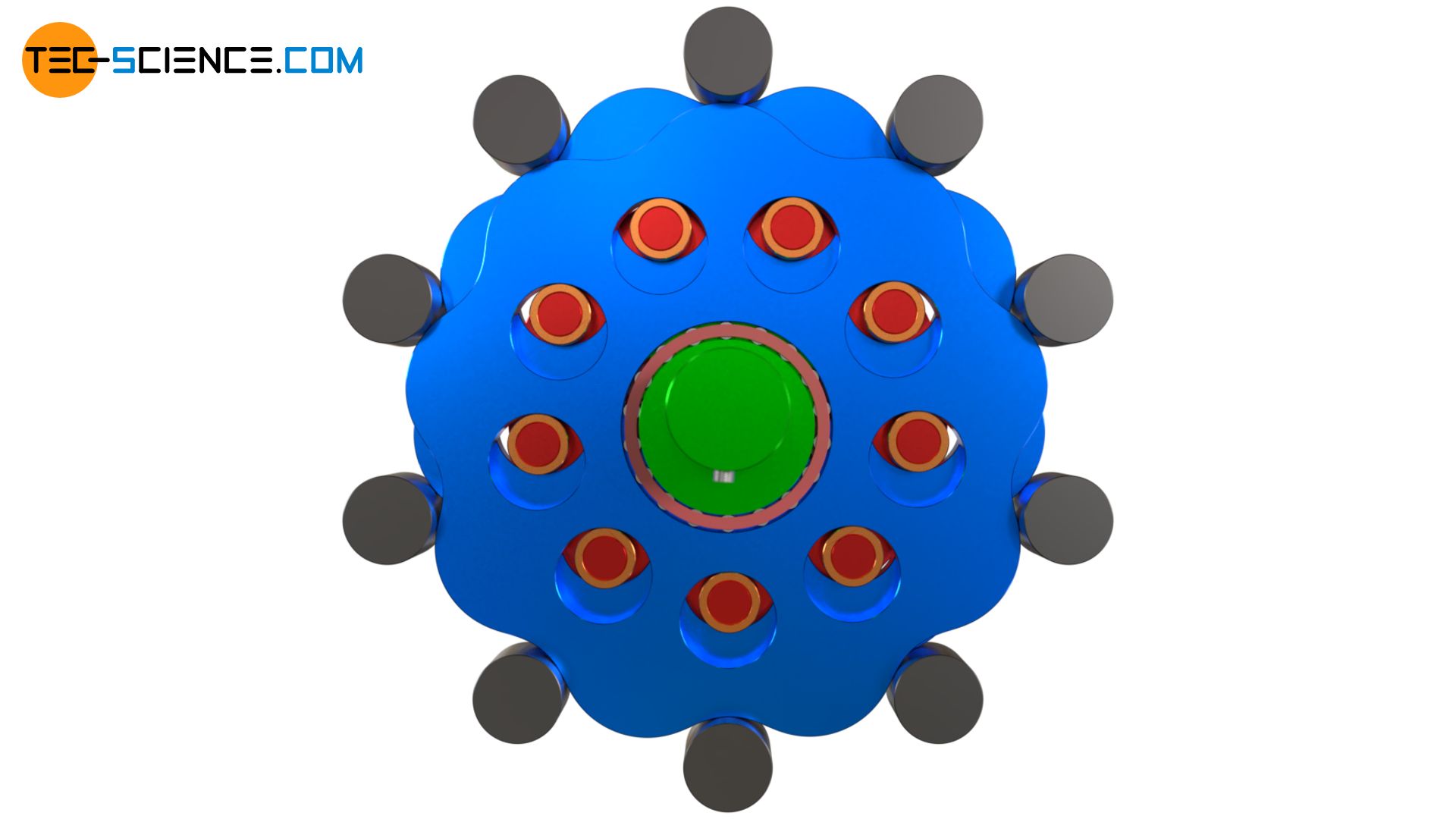
Veranschaulichung der Funktionsweise
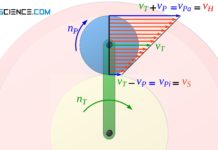
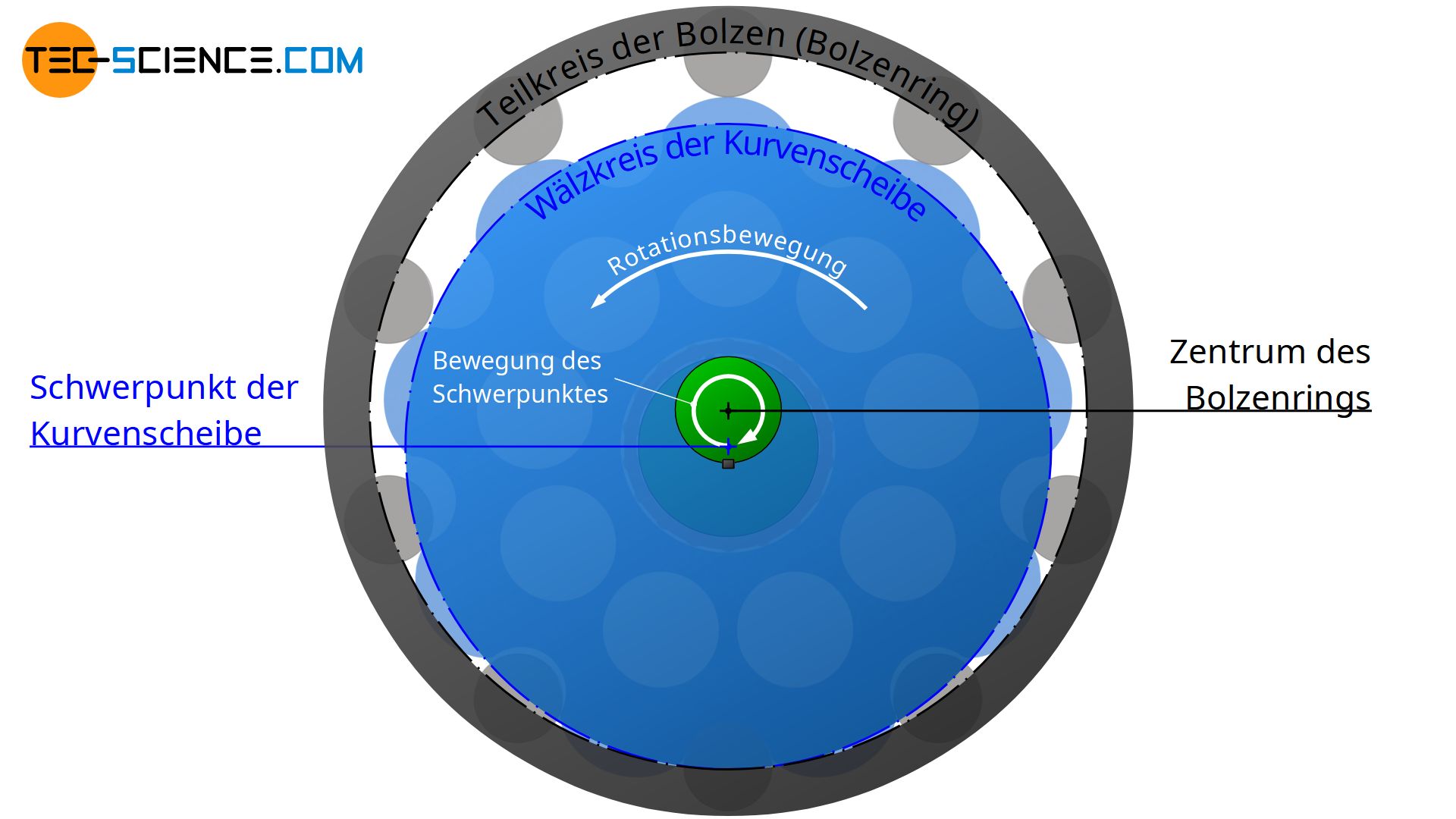
Der Bewegungsablauf eines Zykloidgetriebes erscheint auf den ersten Blick sehr komplex. Die Idee dahinter, die zu einer solchen Kinematik führt, ist jedoch recht einfach. Hierzu stelle man sich zunächst einen Ring vor (Wälzring), auf dessen Innenseite eine Scheibe abwälzt (Wälzscheibe). Die Wälzscheibe wird dabei mithilfe einer Exzenterwelle um die Innenseite des Wälzrings getrieben. Der Wälzring rotiert somit um seine Symmetrieachse entgegen dessen Schwerpunktsbewegung.
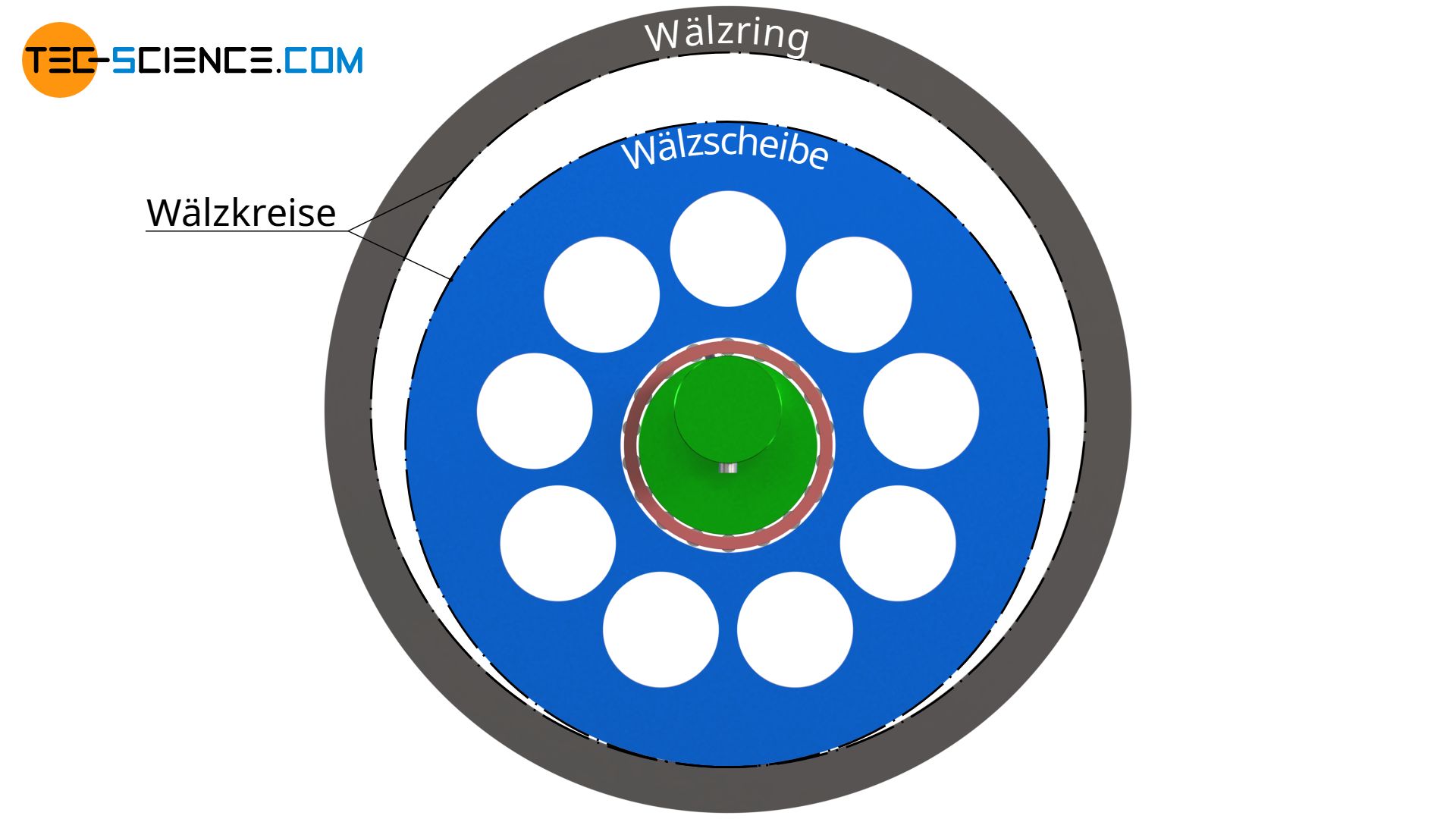
Ein solches Wälzgetriebe erlaubt bisher noch keine große Kraftübertragung, da die Kraftübertragung lediglich durch Reibschluss zwischen den Wälzkörpern zustande kommt. Ein Formschluss ist an dieser Stelle von deutlichem Vorteil. Dies wird durch eine entsprechende Verzahnung zwischen Wälzring und Wälzscheibe erzielt.
Als Zahnform für die Wälzscheibe wird dabei die Zykloide verwendet. Der Wälzkreis der Wälzscheibe dient als Grundkreis für die Konstruktion der Zykloide. Der Wälzring wiederum dient als Teilkreis auf dem die Bolzen befestigt werden, in die dann die Zykloidenscheibe eingreift.
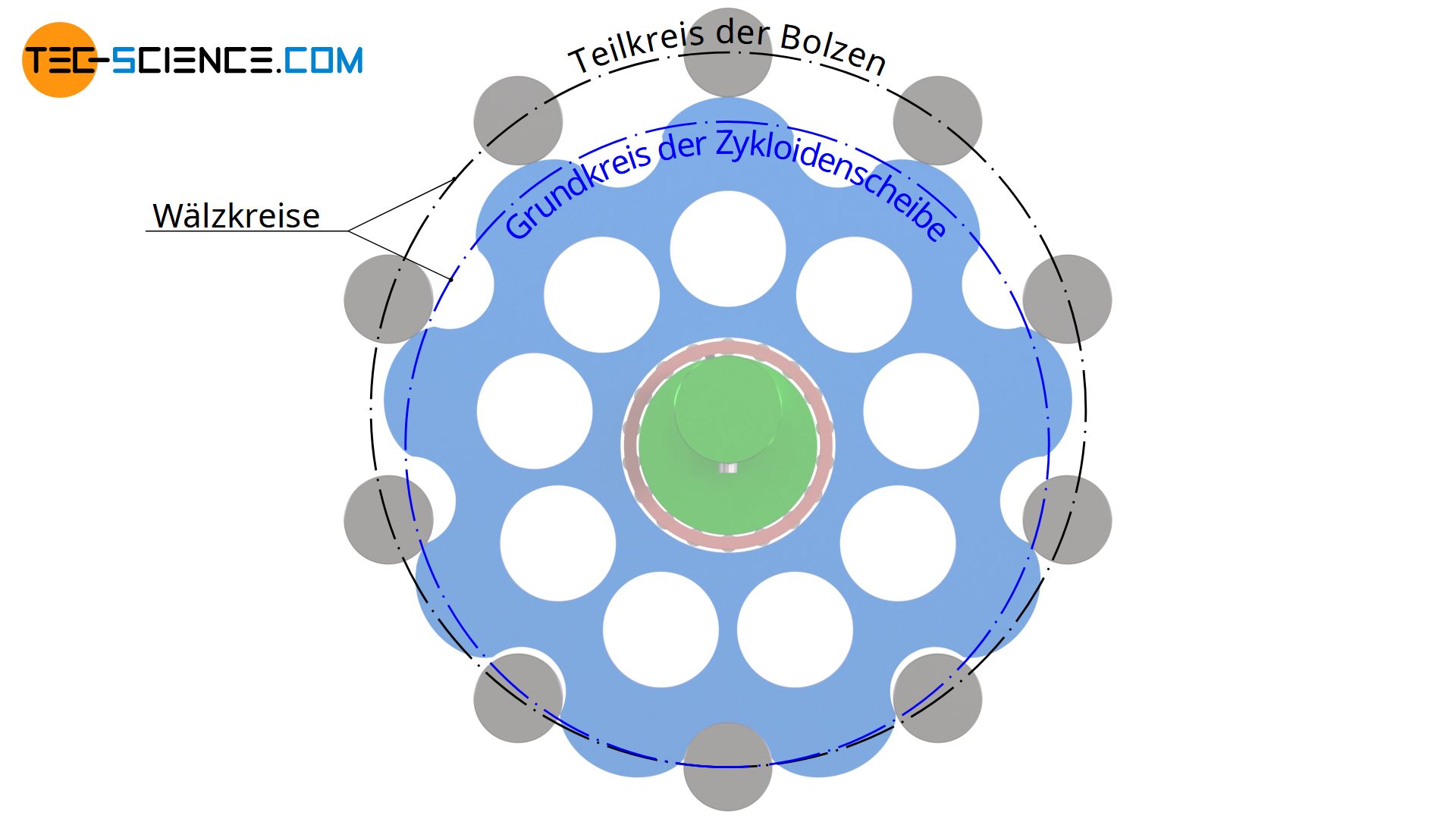
Übersetzungsverhältnis
Für die Bestimmung des Übersetzungsverhältnisses eines Zykloidgetriebes ist die Anzahl N der ringförmig angeordneten Bolzen und die Anzahl n der „Vertiefungen“ bzw. der „Nocken“ der Kurvenscheibe relevant. Dabei muss die Anzahl der Vertiefungen der Kurvenscheibe stets kleiner als die Anzahl der Bolzen sein, ansonsten wäre die Kurvenscheibe größer als der Teilkreis der feststehenden Bolzen und die Kurvenscheibe würde gar nicht erst zwischen die Bolzen passen. In den meisten Fällen besitzt die Kurvenscheibe eine Vertiefung bzw. einen Nocken weniger als Bolzen vorhanden sind.
Am Beispiel mit N=10 Bolzen und n=9 Vertiefungen, soll die Berechnung des Übersetzungsverhältnisses im Folgenden hergeleitet werden. Bei einer vollen Umdrehung der Exzenterwelle, hat sich die Kurvenscheibe dann offensichtlich um insgesamt \N=10 Bolzen gewälzt. Da die Kurvenscheibe aber nur n=9 Vertiefungen besitzt, muss sie sich bei einem ganzen Umlauf folglich um eine Vertiefung weiterbewegt haben. Dies entspricht einen Neuntel einer vollen Umdrehung.
Folglich muss sich die Antriebswelle (Exzenterwelle) insgesamt 9 mal drehen, damit die Kurvenscheibe und mit ihr die Abtriebswelle (Rollenscheibe) eine volle Umdrehungen ausführt. Das Übersetzungsverhältnis wäre in diesem Fall also 1:9.
Hätte die Kurvenscheibe bspw. nur n=7 Vertiefungen am Umfang, dann würde sie sich bei einem Umlauf um die N=10 Bolzen um 3 Vertiefungen weiterbewegt haben. Bei einer vollen Umdrehung der Antriebswelle hätte sich die Abtriebswelle dann um 3 mal 1/7 Umdrehungen weiterbewegt. Die Antriebswelle müsste sich dann 7 mal drehen, damit die Abtriebswelle 3 ganze Umdrehung ausführt. Das Übersetzungsverhältnis betrüge in diesem Fall 7:3.
Verallgemeinert man dieses Prinzip, dann lässt sich das Übersetzungsverhältnis eines Zykloidgetriebes offensichtlich wie folgt anhand der Anzahl n der Nocken der Kurvenscheibe und der Differenz zur Anzahl N der Bolzen ermitteln:
\begin{align}
&\boxed{i = \frac{n}{N-n} } \\[5px]
\end{align}
Beachte: Dadurch, dass die Kurvenscheibe auf der Innenseite des Bolzenrings abwälzt, ist die Rotationsbewegung der Kurvenscheibe um ihren Schwerpunkt entgegengesetzt zu dessen kreisförmiger Schwerpunktsbewegung. Deshalb macht die Kurvenscheibe keine volle Umdrehung bei ihrem Umlauf um die Bolzen. Dies wäre nur dann der Fall, wenn die Kurvenscheibe auf der Außenseite des Bolzenrings abwälzen würde (Rotationsbewegung und Schwerpunkgsbewegung wären dann identisch).
Zykloidgetriebe vs. Planetengetriebe
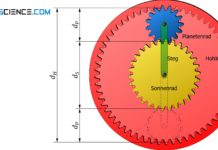
Wenn es um große Übersetzungsverhältnisse bei gleichzeitig kompakter Bauweise geht, dann bieten sich zwei Getriebevarianten besonders an: Das Planetengetriebe und das Zykloidgetriebe. Die Ähnlichkeiten zwischen beiden Getriebearten werden besonders deutlich, wenn das Hohlrad des Planetengetriebes fixiert wird und Antrieb über das Sonnenrad erfolgt und der Abtrieb über den Planetenträger. Beide Getriebearten besitzen umlaufende Achsen und zählen somit im Prinzip zu den Umlaufgetrieben.
Im Falle des Planetengetriebes sind die umlaufenden Achsen die Achsen der Planetenräder und im Falle des Zykloidgetriebes die Achsen der Kurvenscheiben (Zykloidenscheiben). Während die Planetenräder von einem Sonnenrad angetrieben werden, bewegen Exzenter die Zykloidenscheiben. Die Planetenräder bewegen sich bei ihrer Rotation um das Innere eines Hohlrades und die Zykloidenscheiben umlaufen die Bolzen eines Bolzenrings. Die Planetenräder treiben somit letztlich den Planetenträger an auf dem sie sitzen und geben ihre Leistung an die damit verbundene Abtriebswelle ab. Auf die analoge Weise treiben die Zykloidenscheiben eine Rollenscheibe an, die ihrerseits die Leistung dann an die damit verbundene Abtriebswelle abgibt.
| Planetengetriebe | Zykloidgetriebe | |
| unlaufende Achsen | Planetenräder | Kurvenscheiben |
| werden angetrieben von | Sonnenrad | Exzenter |
| umlaufen dabei | Hohlrad | Bolzen |
| treiben hierdurch an | Planetenträger (Steg) | Rollenscheibe |
Zykloidgetriebe weisen gegenüber Planetengetriebe eine sehr große Robustheit gegenüber stoßartigen Belastungen auf. Darüber hinaus erzielen Zykloidgetriebe durch ihr sehr geringes Spiel und ihre hohe Torsionssteifigkeit eine deutlich bessere Positioniergenauigkeit. Deshalb eignen sich Zykloidgetriebe hervorragend für alle Arten von Antriebstechniken (z.B. Robotik bei Servomotoren) und dies besonders bei großen Lasten.
Vor allem bei großen Übersetzungsverhältnissen sind Zykloidgetriebe im Allgemeinen leichter und kompakter als Planetengetriebe und weisen eine höhere Lebensdauer auf. Bei relativ geringen Übersetzungsverhältnissen von unter 20 bieten je nach Anwendung jedoch Planetengetriebe meist die besseren Vorteile und weisen einen höheren Wirkungsgrad auf.